Тема: Принадлежность точки - линии, плоскости, поверхности. Пересечение прямой и плоскости, с плоскостью, поверхностью.

План лекции

1. Принадлежность точки – прямой, плоскости.

2. Принадлежность точки поверхности.

3. Пересечение прямой с плоскостью.

4. Пересечение плоскостей.

5. Пересечение прямой и плоскости с поверхностью.

Точка на прямой

Если известно, что точка принадлежит прямой (например, точка С принадлежит прямой АВ), то горизонтальная проекция точки находится на горизонтальной проекции данной прямой, фронтальная проекция этой точки находится на фронтальной проекции прямой (рис. 1).

Рис. 1

Следы прямой

Точка пересечения прямой с плоскостью проекций называется следом прямой.

Точка пересечения прямой с фронтальной плоскостью проекций называется фронтальным следом прямой.

Точка пересечения с горизонтальной плоскостью проекций называется горизонтальным следом прямой.

На рисунке 2 показаны точки Н и F, в которых прямая, заданная отрезком АВ пересекает плоскости проекций π₁ и π₂.

Горизонтальная проекция Н′ горизонтального следа Н совпадает с этим следом, а его фронтальная проекция Н′′ лежит на оси проекций х.

Фронтальная проекция F′′ фронтального следа F совпадает с этим следом, а его горизонтальная проекция F′ лежит на той же оси проекций – х.

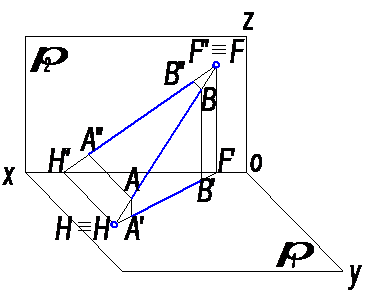
Рис. 2

Чтобы найти горизонтальный след прямой АВ, надо продолжить фронтальную проекцию А′′В′′ до пересечения с осью «х» и через найденную фронтальную проекцию Н′′ горизонтального следа Н, провести линию связи проекций Н′′ и Н′ до пересечения с продолжением горизонтальной проекции А′В′, что определит горизонтальную проекцию Н′ горизонтального следа Н, которая совпадает с самим следом (H′≡H), (рис. 3).

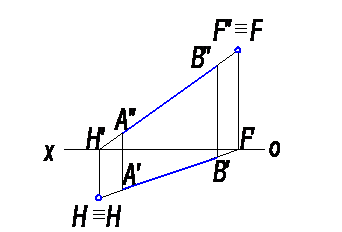
Рис. 3

Для нахождения фронтального следа продолжаем горизонтальную проекцию А′В′ до пересечения с осью х и найденную горизонтальную проекцию F′ фронтального следа F проводим линию связи проекций F′ и F′′ до пересечения с продолжением фронтальной проекции А′′В′′, что обозначит фронтальную проекцию F′′ фронтального следа F, которая совпадает с самим следом (F′′≡F).

Если плоскости проекций принять за плоскости координат, то у горизонтального следа прямой координата z = 0, у фронтального следа – у = 0.

По положению точек Н и F можно судить, к каким четвертям пространства отнесена данная прямая. На рисунке 3 прямая АВ проходит через, I, II, IV четверти.

Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.

Прямая в плоскости

Построение прямой линии в плоскости основано на двух положениях, известных из геометрии:

1) прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.

2) прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости и параллельна прямой, находящейся в этой плоскости или параллельной ей.

Допустим, что плоскость α определена двумя пересекающимися прямыми АВ и ВС, а плоскость β двумя параллельными прямыми DE и FG (рис. 4).

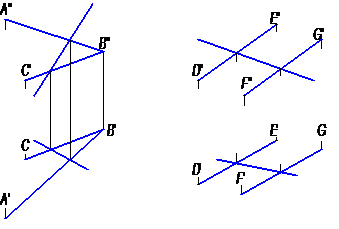
Рис.4

Согласно первому положению прямая, пересекающая прямые, определяющие плоскость, находится в данной плоскости.

Отсюда следует, что, если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных следах плоскости (рис. 5).

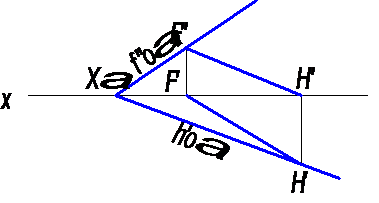
Рис.5

Из второго положения следует, что прямая принадлежит плоскости, если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку (рис. 6).

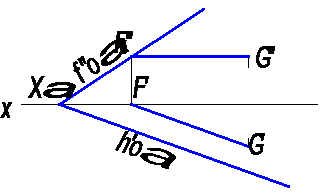
Рис.6

Точка в плоскости

Чтобы построить на чертеже точку, лежащую в заданной плоскости, надо построить прямую, лежащую в этой плоскости и отметить на этой прямой точку.

Рассмотрим задачу. Известно, что точка М расположена в плоскости α (а∩в). Задана фронтальная проекция этой точки – М′′. Определить горизонтальную проекцию точки – М′(рис. 7).

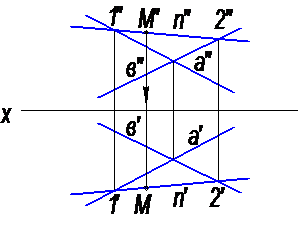
Рис. 7

Чтобы найти горизонтальную проекцию точки – М′, через ее фронтальную проекцию проведем фронтальную проекцию прямой – n′′ так, чтобы она пересекала фронтальные проекции прямых а′′ и в′′. По фронтальным проекциям точек пересечения – 1′′ и 2′′ определятся их горизонтальные проекции, затем через точки 1′ и 2′ строится горизонтальная проекция прямой – n′. Проведя из точки М′′ линию связи, получим горизонтальную проекцию точки – М′.

Точка М принадлежит плоскости α (а∩в), т. к. она расположена на прямой n, лежащей в этой плоскости.