Поверхность на чертеже. Гранные поверхности. Поверхности вращения.

Многогранником называется замкнутая пространственная фигура, ограниченная плоскими многоугольниками. Форму многогранников имеют многие детали сельскохозяйственных машин и инструменты.

Наибольший практический интерес представляют призмы, пирамиды и выпуклые однородные многогранники – тела Платона (тетраэдр, гекаэдр, октаэдр, додекаэдр, икосаэдр), а также и многие другие многогранники.

Кратко охарактеризуем геометрические свойства наиболее распространенных многогранников.

ПИРАМИДА – это многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной. Пирамиду называют правильной, если основанием ее является правильный многоугольник и высота пирамиды (перпендикуляр, опущенный из вершины на основание) проходит через центр этого многоугольника.

Пирамида называется усеченной, если вершина её отсекается плоскостью, пересекающей все ребра, исходящие из этой вершины.

На эпюре пирамида задается проекциями ее основания и вершины (рис. 31), а усеченная пирамида проекциями обоих оснований (рис. 32).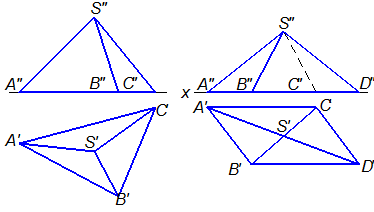

Рис. 31

ПРИЗМОЙ называют многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно- параллельными сторонами, все другие грани – параллелограммы (рис. 33).

Призму называют прямой, если ребра её перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллепипедом(рис. 34).

Выбирая положение призмы или пирамиды для изображения, целесообразно располагать их основания параллельно плоскости проекций.

Для пирамиды достаточно двух проекций при условии, что на одной из них показана форма основания.

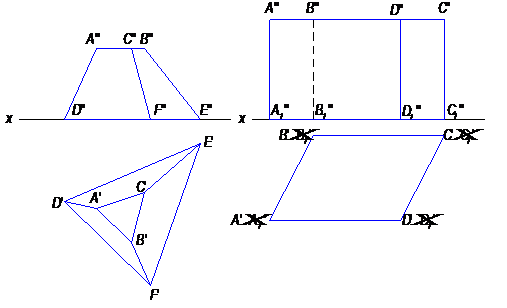
Рис. 32 Рис. 33

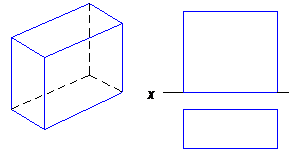
Рис. 34

Видимость ребер определяется по расположению конкурирующих точек, принадлежащих ребрам (рис. 35).

Чтобы определить видимость горизонтальной проекции ребра SA пирамиды SABC, нужно провести проецирующий луч S₁. Точка 1, принадлежащая ребру SA, расположена выше, чем точка 2, принадлежащая ребру SC. Отсюда ясно, что горизонтальная проекция точки 1 будет видимой, а горизонтальная проекция точки 2 – невидимой. Следовательно, и горизонтальная проекция ребра SA будет видимой.

Чтобы определить видимость фронтальной проекции ребра SC, проведем проецирующий луч S₂. Точка 3, расположенная на стороне АВ основания пирамиды SABC, находится к наблюдателю ближе, чем точка 4 на ребре SC. Отсюда ясно, что фронтальная проекция точки 3 будет видимой, а фронтальная проекция точки 4 – невидимой; Следовательно, фронтальная проекция ребра SC будет невидимой.

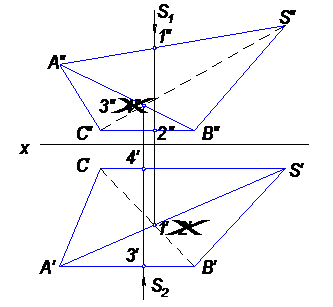
Рис. 35

Поверхности вращения

Поверхностью вращения общего вида называют поверхность, которая образуется произвольной прямой или кривой (плоской или пространственной) при ее вращении вокруг неподвижной оси.

Каждая точка образующей при вращении вокруг оси описывает окружность с центром на оси вращения. Эти окружности называют параллелями. Наибольшую параллель называют экватором.

Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, – меридианами. Меридиональную плоскость, параллельную плоскости проекций π₂, принято называть главной меридиональной плоскостью, а линию пересечения с поверхностью вращения – главным меридианом.

При задании поверхности вращения на чертеже обычно указывают проекции ее оси, главного меридиана и экватора.

В технике, в частности в машиностроении, поверхности вращения находят широкое применение. Это объясняется распространенностью вращательного движения на станках.

Особенно распространены поверхности, имеющие в меридиональном сечении кривую второго порядка или две прямые, на которые распадается эта кривая.

Некоторые поверхности вращения представляют собой частные случаи поверхностей, в качестве образующей которых является окружность. В зависимости от взаимного расположения окружности (или ее дуги) и оси вращения можно получить различные поверхности:

1) тор(рис. 36 – 38);

тором называется поверхность, которая может быть получена при вращении окружности вокруг оси, не проходящей через ее центр.

В зависимости от соотношения величин R – радиуса образующей окружности и расстояния t от центра окружности до оси вращения поверхности тора подразделяют:

а) открытый тор (или кольцо) при R<t – окружность не пересекает ось вращения(рис.36);

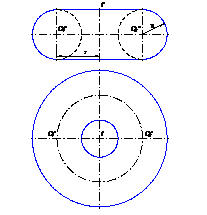
Рис. 36

б) замкнутый тор, R = t(рис.37);

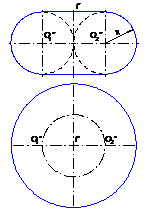
Рис.37

в) самопересекающийся тор, R>t(рис.38);

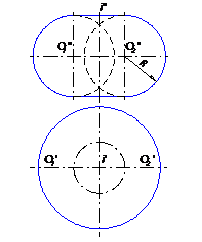
Рис.38

2)цилиндр вращения(рис.39);

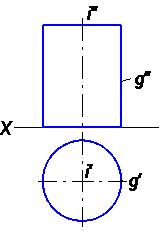
Рис.39

3) конус вращения(рис.40);

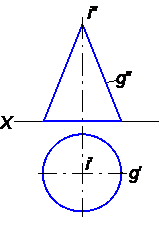
Рис.40

Для цилиндра и конуса вращения меридианы являются прямыми линиями – в первом случае параллельными оси и равноудаленными от нее, во втором случае пересекающими ось в одной и той же точке, под одним и тем же углом к оси.

Меридиан цилиндра на рисунке 39 – прямоугольник, а конуса на рисунке 40 – треугольник.

4) сфера(рис.41);

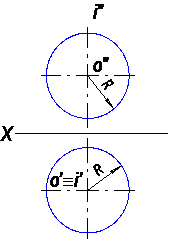
Рис. 41

Сфера образуется в том случае, когда центр окружности принадлежит оси вращения. Сферу можно рассматривать как частный случай тора, у которого t=0.

5) гиперболоид вращения (рис. 42);

Для гиперболоида вращения меридианом является гипербола, причем если осью вращения служит действительная ось гиперболы, то образуется двуполостный гиперболоид вращения; если же вращать гиперболу вокруг её мнимой оси, то однополостный.

Однополостный гиперболоид вращения может быть образован также вращением прямой линии в случае, если образующая и ось вращения – скрещивающиеся прямые. На рисунке 42 показан однополостный гиперболоид вращения, образованный вращением прямой АВ вокруг указанной оси и ограниченный двумя параллелями. На однополостном гиперболоиде вращения можно нанести прямолинейные образующие в двух направлениях, например так, как показано на рисунке 42, и с наклоном в обратную сторону, под тем же углом к оси.

Кроме прямых (пар) на этой поверхности могут быть ещё гиперболы, параболы, эллипсы и окружности.

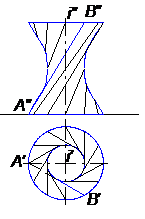
Рис. 42

Для параболоида вращения меридианом является парабола, ось которой служит осью поверхности.

Для эллипсоида вращения меридианом является эллипс. Поверхность может быть образована вращением эллипса вокруг его большой оси («вытянутый» эллипсоид вращения) или вокруг его малой оси («сжатый» эллипсоид вращения) (рис. 43).

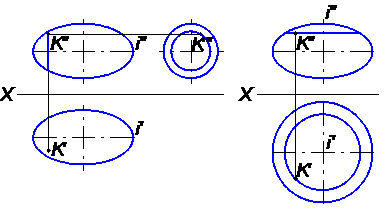
а) «вытянутый» эллипсоид б) «сжатый» эллипсоид

Рис. 43

Контрольные вопросы

1. В чем заключается способ образования эпюра Монжа?

2. Что позволяют определять конкурирующие точки?

3. Назовите положение прямых.

4. Как можно задать плоскость на чертеже?

5. Что такое след плоскости?

6. Назовите положение плоскостей.

7. Какие главные линии плоскости вы знаете?

8. Какая поверхность называется многогранником? Какие гранные поверхности вы знаете.

9. Как определяется видимость ребер многогранника?

10. Как определяется не6достающая проекция точки принадлежащей многограннику?

11. Что называется поверхностью вращения? Какие поверхности вращения вы знаете?

12. Как определяется недостающая проекция точки принадлежащей поверхности вращения?

Рекомендуемая литература

1. Фролов, С.А. Начертательная геометрия: Учебник. 3-е изд., перераб. и доп. – М.: ИНФРА, 2010. – 285 с.

1. Чекмарев А.А. Начертательная геометрия и черчение: Учеб.для студ. высш. учеб. Заведений. – 2 – е изд., перераб. и доп. – М.: Гуманит. изд. центр ВЛАДОС, 2005. – 471 с.: ил.

3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М.: Высш. шк., 2009. – 272 с.:ил.

4. Петлина Т.П. Начертательная геометрия. Ортогональные проекции и их преобразование: Учеб.пособие (с примерами практического использования в курсовом и дипломном проектировании). – Самара: СамВен, 2005. – 168 с.

Лекция 2