Глава 8. чтение чертежей общего вида и их
Конспект лекций по курсу
Инженерная и компьютерная графика
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ............................................................................................... 3
ПРЕДИСЛОВИЕ............................................................................................. 6
ОБОЗНАЧЕНИЯ............................................................................................. 6
Глава 1. МЕТОД ПРОЕКЦИЙ............................................................... 6
1.1. Центральное, параллельное и ортогональное проецирование.............. 7
1.2. Эпюр Монжа или комплексный чертеж.................................................. 7
1.3. Построение проекций точки по ее координатам .................................... 8
Вопросы для самоконтроля, тесты ................................................................ 9
Глава 2. ПРЯМАЯ....................................................................................... 10
2.1. Прямые частного и общего положения................................................. 10
2.1.1. Прямые уровня..................................................................................... 10
2.1.2. Проецирующие прямые....................................................................... 11
2.1.3. Прямая общего положения................................................................. 12
2.2. Определение натуральной величины отрезка прямой и углов наклона
его к плоскостям проекций методом прямоугольного треугольника. 12
2.4. Взаимное положение прямых в пространстве. Конкурирующие
точки. Видимость................................................................................... 13
Вопросы для самоконтроля, тесты .............................................................. 14
Глава 3. ПЛОСКОСТЬ.......................................................................... 15
3.1. Способы задания плоскости на чертеже............................................... 15
3.2. Плоскости частного и общего положения............................................. 15
3.2.1. Плоскости уровня................................................................................ 15
3.2.2. Проецирующие плоскости.................................................................. 16
3.2.3. Плоскости общего положения........................................................... 16
3.3. Принадлежность точки и прямой плоскости........................................ 17
3.4. Главные линии плоскости...................................................................... 17
3.5. Взаимное положение прямых и плоскостей.......................................... 18
3.5.1. Параллельность прямых и плоскостей.............................................. 18
3.5.2. Перпендикулярность прямых и плоскостей....................................... 19
3.6. Позиционные задачи на плоскости........................................................ 19
3.6.1. Пересечение прямой и плоскости....................................................... 20
3.6.2. Пересечение плоскостей. Метод вспомогательных секущих
плоскостей.......................................................................................... 21
Вопросы для самоконтроля, тесты .............................................................. 23
Глава 4. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА................... 24
4.1. Способ вращения вокруг проецирующей оси...................................... 24
4.2. Способ плоскопараллельного перемещения......................................... 25
4.3. Способ замены плоскостей проекций.................................................... 26
4.3.1. Определение длины отрезка общего положения............................... 27
4.3.2. Определение натуральной величины плоской фигуры....................... 28
Вопросы для самоконтроля, тесты .............................................................. 29
Глава 5. МНОГОГРАННИКИ.............................................................. 29
5.1. Образование поверхностей многогранников........................................ 29
5.2. Точка и линия на поверхности многогранника.................................... 30
5.3. Позиционные задачи.............................................................................. 31
5.3.1. Пересечение многогранника прямой................................................... 32
5.3.2. Натуральная величина сечения.......................................................... 33
5.3.3. Пересечение двух многогранников....................................................... 34
5.4. Развертка многогранника...................................................................... 35
5.4.1. Развертка призмы. Методы нормального сечения и раскатки........ 35
5.4.2. Развертка пирамиды методом треугольников (триангуляции)....... 36
Вопросы для самоконтроля, тесты .............................................................. 37
Глава 6. КРИВЫЕ ПОВЕРХНОСТИ.................................................... 38
6.1. Поверхности вращения.......................................................................... 38
6.2. Точка и линия на поверхностях вращения........................................... 40
6.2.1. Конус.................................................................................................... 40
6.2.2. Сфера................................................................................................... 41
6.3. Пересечение поверхности вращения и многогранника....................... 42
6.4. Пересечение поверхностей вращения. Метод вспомогательных секущих концентрических сфер................................................................................... 44
6.5. Развертка цилиндра и конуса................................................................ 46
Вопросы для самоконтроля,тесты ............................................................... 47
Глава 7. ПРАВИЛА ВЫПОЛНЕНИЯ СБОРОЧНОГО
ЧЕРТЕЖА И ЭСКИЗОВ ДЕТАЛЕЙ..................................................... 48
7.1. Эскиз детали и его назначение............................................................... 48
7.2. Требования, предъявляемые к выполнению эскизов............................ 48
7.3. Выбор главного изображения............................................................... 61
7.4. Назначение и основные требования, предъявляемые к
сборочному чертежу............................................................................. 49
7.5. Последовательность выполнения сборочного чертежа........................ 50
7.6. Составление спецификации.................................................................... 50
7.7. Выбор количества изображений........................................................... 51
7.8. Нанесение размеров сборочного чертежа............................................ 53
Вопросы для самоконтроля,тесты ............................................................... 53
Глава 8. ЧТЕНИЕ ЧЕРТЕЖЕЙ ОБЩЕГО ВИДА И ИХ
ДЕТАЛИРОВАНИЕ................................................................................. 54
8.1. Чтение чертежей общего вида................................................................ 54
8.1.1.Последовательность чтения чертежей общего вида........................ 54
8.2. Деталирование........................................................................................ 55
Вопросы для самоконтроля,тесты ............................................................... 57
Глава 9. РАБОТА В ГРАФИЧЕСКОМ РЕДАКТОРЕ
КОМПАС-ГРАФИК ............................................................................... 58
9.1. Объекты главного окна ......................................................................... 58
9.2. Команды меню........................................................................................ 60
9.3. Панели кнопок........................................................................................ 61
9.4. Привязки ................................................................................................ 63
9.4.1. Локальные привязки ........................................................................... 64
9.4.2 Глобальные привязки............................................................................ 64
9.5. Стстемы координат ............................................................................... 65
9.5.1. Абсолютная система координат ...................................................... 65
9.5.2. Локальные системы координат......................................................... 65
Контрольные задания к разделу ................................................................. 67
ЛИТЕРАТУРА............................................................................................. 69
СЛОВАРЬ ТЕРМИНОВ............................................................................. 69
ТЕСТЫ ПО КУРСУ .................................................................................. 70
ОТВЕТЫ НА ТЕСТЫ ПО КУРСУ ......................................................... 74
ЗАЧЕТНЫЕ ЗАДАНИЯ.............................................................................. 75
ПРЕДИСЛОВИЕ
В настоящее время по курсу «Начертательная геометрия. Инженерная и компьютерная графика» опубликовано большое количество учебников и пособий, охватывающих значительный объем излагаемых вопросов, в той или иной степени подробно освещающих все разделы указанного предмета.
Предлагаемое пособие содержит в себе основы трех дисциплин, изучаемых в техническом вузе: начертательной геометрии, науки изучающей способы изображения пространственных фигур на плоском чертеже; инженерной графики, задачей которой является овладение студентами знаний о законах построения графических объектов на плоскости с соблюдением требований Единой Системы Конструкторской Документации (ЕСКД) и компьютерной графики, дисциплины, позволяющей получить навыки выполнения чертежей с использованием графического редактора (Компас-График 5.9 LT).
Несмотря на небольшой объем, пособие содержит множество примеров и иллюстраций и служит эффективным средством для решения практических задач, на что оно главным образом и ориентировано.
Материал изложен в сжатой форме доступным языком.
ОБОЗНАЧЕНИЯ
Приводятся обозначения, используемые в данном учебном пособии.
П1, П2, П3 – горизонтальная, фронтальная, профильная плоскости проекций;
П4 , П5, … – дополнительные плоскости проекций;
Δ, Ω, Σ, Г, Ф,… – произвольные плоскости общего и частного положений;
а, в, с,… – прямые линии;
а1, в2, с3 – проекции прямых а, в, с на горизонтальную, фронтальную и профильную плоскости проекций соответственно;
h, f, p – прямые уровня (горизонталь, фронталь и профильная соответственно);
А, В, С, …, 1, 2, 3,… – точки (обозначаются прописными латинскими буквами и арабскими цифрами);
А1, В2, С3, … проекции точек А, В, С на горизонтальную, фронтальную и профильную плоскости проекций соответственно;
α, β, γ – плоские углы;
ОХ, OY, OZ – оси проекций.
Глава 1. Метод проекций
Правила построения изображений, излагаемые в курсе начертательной геометрии, основаны на методе проекций. Рассмотрение метода проекций начинают с построения проекции точки, на примере которого рассматривают все базовые понятия и правила проецирования.
1.1. Центральное, параллельное и ортогональное проецирование
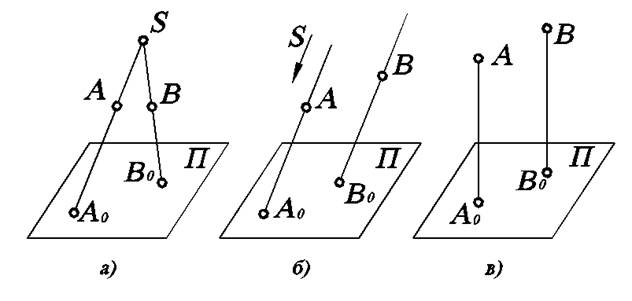
Наиболее общим методом проецирования является центральное проецирование (рис.1.1а). Сущность центрального проецирования заключается в следующем: пусть даны плоскость П и точка S (SÏП). Возьмем произвольную точку А (АÏП, АÏS). Через заданную точку S и точку А проводим прямую SА и отмечаем точку А0, в которой эта прямая пересекает плоскость П. Плоскость П называют плоскостью проекций , точку S центром проецирования, полученную точку А0 – центральной проекцией точки А на плоскость П, прямую SА – проецирующей прямой. Аналогично можно получить проекцию любой другой точки.
Частным случаем центрального проецирования является параллельное (рис. 1.1б), когда центр проецирования находится в бесконечности. Тогда проецирующие лучи параллельны друг другу.
Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций (рис. 1.1в), называется ортогональным проецированием.
 |
В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение всех чертежей основано на этом методе.
Рис. 1.1. Методы проецирования: а) центральное; б) параллельное; в) ортогональное.
1.2. Эпюр Монжа или комплексный чертеж
Проекция геометрического объекта на одну плоскость не дает полного и однозначного представления о самом геометрическом объекте. Рассмотрим проецирование на три взаимно перпендикулярные плоскости (рис. 1.2), одна из которых расположена горизонтально, а две другие вертикально.
Тогда плоскость П1 называется горизонтальной плоскостью проекций, П2 - фронтальной плоскостью проекций (т.к. она расположена перед нами по фронту), П3 - профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю). Соответственно А1 - горизонтальная проекция точки А, А2 -фронтальная проекция точки А, А3 - профильная проекция точки А. Оси ОХ, ОY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево.
Несмотря на наглядность, с чертежом, изображенным на рис 1.2а работать неудобно, т.к. плоскости на нем показаны с искажениями. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость проекций развернуть вокруг оси ОХ на 90° и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя вверх. После чего профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. Этот метод предложил Г. Монж. В результате полученное изображение называют трехкартинный комплексный чертеж (эпюр Монжа), рис. 1.2б. Так как ось ОY разворачивается вместе с двумя плоскостями П1 и П3, то на комплексном чертеже ее изображают дважды.
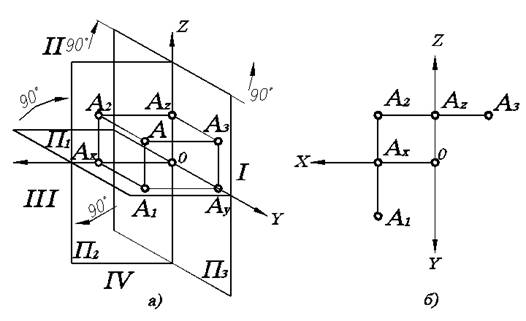
Рис. 1.2. Построение эпюра Монжа:
а) пространственная картина расположения проекций точки А; б) трехкартинный комплексный чертеж
Из этого следует важное правило взаимосвязи проекций. А именно, исходя из рис. 1.2а очевидно А1Аx = ОАy = АzА3. Следовательно, это правило можно сформулировать так: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции точки до оси ОZ. Тогда по двум любым проекциям точки можно построить третью.
1.3. Построение проекций точки по ее координатам
Если заданы координаты какой-либо точки А (x, y, z), тогда проекции точки строят следующим образом: сначала откладывают абсциссу по оси ОХ; затем проводят вертикальную линию; далее на ней откладывают ординату по оси OY и аппликату по оси OZ. По оси OY получают горизонтальную проекцию А1, по оси OZ - фронтальную А2. Профильную проекцию А3 строят по А1 и А2 (либо по координатам). Например, построим проекции точек А (10, 20, 30).Построения показаны на рис. 1.3.
Необходимо помнить, что положение горизонтальной проекции определяется координатами х и y, фронтальной - координатами х и z, профильной – координатами y и z. Тогда ордината y всегда характеризует положение горизонтальной проекции, а аппликата – фронтальной.
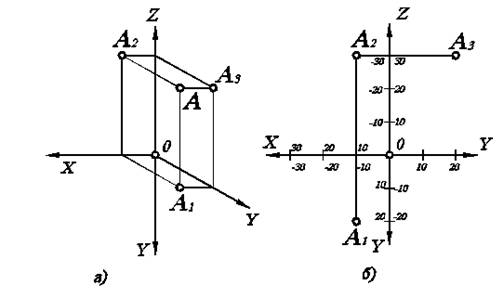
Рис.1.3. Взаимосвязь координат точки и ее проекций: а) вид в аксонометрии; б) комплексный чертеж.
Исходя из тех же положений, решается обратная задача – определение координат точки по ее проекциям. Если на комплексном чертеже изображены проекции точки, тогда, измерив соответствующие расстояния, определяем ее координаты (см. рис. 1.3б). Причем для определения всех трех координат достаточно двух проекций, т.к. любая пара проекций определяет три координаты.
Вопросы для самоконтроля
1. Какие виды проецирования существуют ?
2. В чем заключается метод Г. Монжа ?
3. Понятие комплексного чертежа или эпюра ?
4. Каким образом определяют удаленность точек от плоскостей проекций?
Тестовые задания
1. Фронтальная плоскость проекций обозначается:
а) П2; б) П3; в) П1.
2. Профильная проекция точки определяется координатами:
а) (х; у); б) (у; z); в) (х; z).
3. Какие координаты будет иметь точка, принадлежащая фронтальной плоскости проекций ?
а) (х; y; 0); б) (0; у; z); в) (х; 0; z).
Глава 2. Прямая
Поскольку положение прямой в пространстве однозначно определяется двумя точками, то и для определения положения проекций прямой также достаточно зафиксировать проекции двух точек. Поэтому для построения проекций прямой можно использовать все правила, касающиеся проецирования точки.
2.1. Прямые частного и общего положения
2.1.1. Прямые уровня
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.
Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.
а)Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонтальной прямой уровня или горизонталью и обозначается h.
б) Прямая, параллельная фронтальной плоскости проекций П2, называется фронтальной прямой уровня или фронталью и обозначается f.
в) Прямая, параллельная профильной плоскости проекций П3, называется профильной линией уровня и обозначается p.
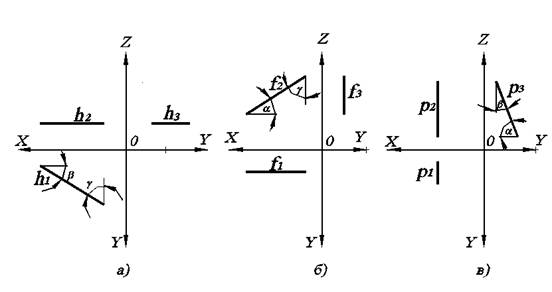
Рис. 2.1. Линии уровня на комплексном чертеже: а) горизонтальная; б) фронтальная; в) профильная.
Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.
Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h1, f2, p3 – это натуральная величина соответствующих прямых h, f, p.
a - угол наклона прямой уровня к П1,
b - угол наклона прямой уровня к П2,
g - угол наклона прямой уровня к П3.
2.1.2. Проецирующие прямые
Проецирующей прямой называется прямая перпендикулярная одной из плоскостей проекций, а следовательно, параллельная двум другим плоскостям проекций.
Исходя из положения проецирующих прямых в пространстве, их проекции выглядят как показано на рис. 2.2.
а)Прямая, перпендикулярная горизонтальной плоскости проекций П1, называется горизонтально-проецирующей прямой и обозначается i.
б)Прямая, перпендикулярная фронтальной плоскости проекций П2, называется фронтально-проецирующей прямой и обозначается j.
в)Прямая, перпендикулярная профильной плоскости проекций П3, называется профильно-проецирующей прямой обозначается r.
|
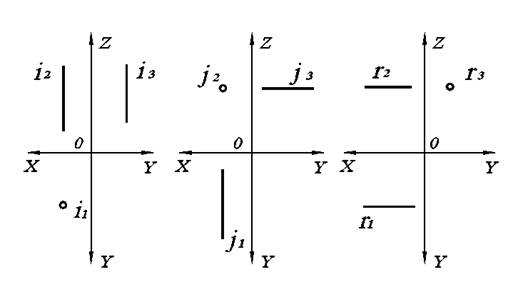
Рис. 2.2. Проецирующие прямые на комплексном чертеже: а) горизонтально-проецирующая; б) фронтально-проецирующая; в) профильно–проецирующая.
У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i2, i3, j1, j3, r1, r2 – это натуральные величины соответствующих прямых i, j, r.
2.1.3. Прямая общего положения
Прямой общего положения называется прямая, занимающая общее положение в пространстве, т.е. не параллельная ни к одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.
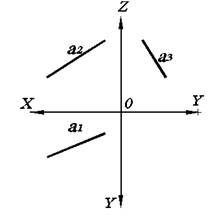
Рис. 2.3. Прямая общего положения на комплексном чертеже.
Естественно, что ни одна из проекций прямой общего положения не показывает ее натуральную величину, а также угол наклона к одной из плоскостей проекций (рис. 2.3).
2.2. Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника
Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который можно сформулировать так: натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которого служит горизонтальная (фронтальная) проекция отрезка, другим – разность расстояний от граничных точек фронтальной (горизонтальной) проекции отрезка до оси ОХ. При этом углом наклона отрезка к горизонтальной (фронтальной) плоскости проекции является угол между гипотенузой прямоугольного треугольника и горизонтальной (фронтальной) проекцией отрезка.
В соответствии с этим построения необходимо выполнять в следующей последовательности. Из любой точки (например, D1) отрезка С1D1 проведем перпендикуляр к нему (рис. 2.4.).
На нем, отложив отрезок длиной Dz, получим точку D*. После соединения точек D* и С1 получаем прямоугольный треугольник С1D1D*, в котором С1D* - натуральная величина отрезка СD, a - угол наклона отрезка СD к плоскости П1. Для определения угла наклона к плоскости П2 проведем аналогичные построения на фронтальной проекции.
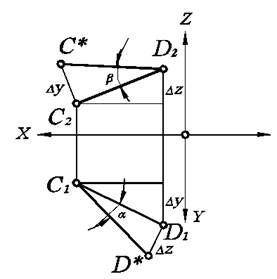
Рис. 2.4. Определение натуральной величины отрезка прямой способом прямоугольного треугольника.
2.3. Взаимное положение прямых в пространстве. Конкурирующие точки
Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: а) быть параллельными; б) пересекаться; в) скрещиваться, т.е. не пересекаться, но и не быть параллельными. Рассмотрим на рис. 2.5 как при этом располагаются их проекции. Поскольку профильные проекции прямых можно построить по двум имеющимся, то на рис. 2.5 ограничимся двухкартинным комплексным чертежом.
В соответствии с одним из свойств ортогонального проецирования, если прямые параллельны, то их одноименные проекции параллельны (рис. 2.5а). Если прямые пересекаются, то их проекции пересекаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А – точка пересечения прямых с и d). Если прямые скрещиваются, то их проекции пересекаются, но точки пересечения проекций не лежат на одной линии проекционной связи (на рис. 2.5в точки С1 и В2) не лежат на одной линии проекционной связи. Тогда, следуя по вертикальной линии связи от точки С1, получим на каждой из прямых n2 и m2 соответственно две проекции: точки С2 и другой точки D2, а следовательно, на пересечении n1 и m1 лежат две точки С1 и D1, слившиеся в одну.
Точки, лежащие на одном проецирующем луче, называются конкурирующими.. Точки, горизонтальные проекции которых совпадают, называются горизонтально–конкурирующими (на рис. 2.5в см. точки C и D), а если совпадают фронтальные проекции, то точки называются фронтально-конкурирующими (на рис. 2.5в - точки В и Е).
При этом конкурирующие точки расположены на разном расстоянии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П2, будет закрыта от наблюдателя точкой, расположенной дальше от П2, а следовательно, ближе к наблюдателю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е – видимая, а точка В – невидимая. Аналогично С – видимая , а D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круглые скобки.
Рис. 2.5. Двухкартинный комплексный чертеж прямых, занимающих по отношению друг к другу следующее положение: а) а êêb; б) с Ç d; в) n ¸ m
Вопросы для самоконтроля
1. Что называется прямой общего положения?
2. Какая прямая называется прямой уровня?
3. Какая прямая называется проецирующей прямой?
4. Какое положение прямые могут занимать в пространстве по отношению друг к другу?
5. Как определить натуральную величину отрезка прямой по ее комплексному чертежу?
Тестовые задания
1. Фронтальная прямая уровня параллельна:
а) П2; б) П3; в) П1.
2. Прямая общего положения по отношению к плоскостям проекций занимает следующее положение:
а) параллельна одной из плоскостей проекций;
б) перпендикулярна одной из плоскостей проекций;
в) не параллельна ни одной из плоскостей проекций.
3. Если прямые в пространстве параллельны:
а) их проекции пересекаются;
б) их проекции параллельны;
в) их проекции имеют общую точку.
Глава 3. Плоскость
Плоскость является простейшей поверхностью, которую можно представить как веер линий, полученных при движении прямой (образующей), закрепленной в некоторой точке, по другой прямой (направляющей).
3.1. Способы задания плоскости на чертеже
Положение плоскости в пространстве может быть однозначно определено одним из хорошо известных в геометрии элементов. В соответствии с этим плоскость может быть задана одним из шести способов:
а) тремя точками, не лежащими на одной прямой;
б) прямой и точкой, не лежащей на этой прямой;
в) двумя параллельными прямыми;
г) двумя пересекающимися прямыми;
д) плоской фигурой;
е) следами.
Тогда на чертеже (рис. 3.1) соответствующие геометрические объекты (точки, прямые) выглядят в виде проекций.
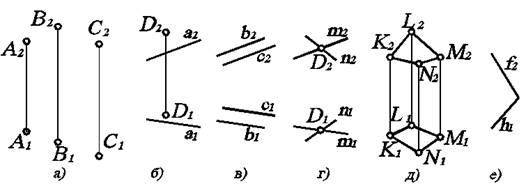
Рис. 3.1. Безосный двухкартинный комплексный чертеж геометрических объектов, задающих плоскость.
3.2. Плоскости частного и общего положения
3.2.1. Плоскости уровня
Плоскостью уровня называется плоскость, параллельная одной из плоскостей проекций, а следовательно, перпендикулярная двум другим. Тогда проекциями плоскости уровня будут прямые, параллельные соответствующим осям (рис. 3.2), вне зависимости от того, чем задана плоскость. От способа задания плоскости зависит лишь ее проекция на ту плоскость проекций, которой заданная плоскость параллельна.
Плоскость, параллельная П1, называется горизонтальной плоскостью уровня ( Г ). На рис. 3.2а она задана тремя точками .
Плоскость, параллельная П2, называется фронтальной плоскостью уровня (Ф). Зададим ее параллельными прямыми (рис. 3.2б).
Плоскость, параллельная П3, называется профильной плоскостью уровня (Р). Считаем ее заданной пересекающимися прямыми (рис. 3.2в).
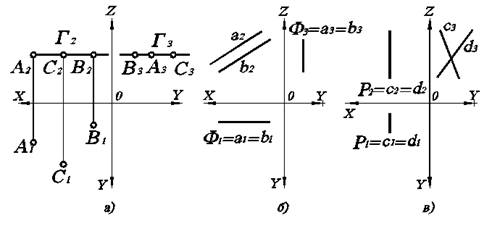
Рис. 3.2. Плоскости уровня на комплексном чертеже.
3.2.2. Проецирующие плоскости
Проецирующей называется плоскость, перпендикулярная одной из плоскостей проекций. Исходя из определения, такая плоскость вырождается в прямую при проецировании на ту плоскость проекций, к которой она перпендикулярна.
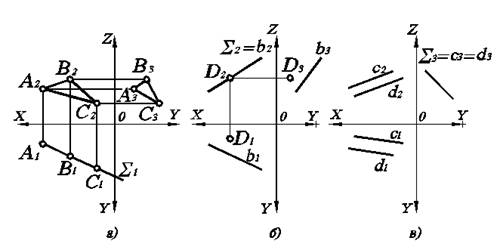
Рис. 3.3. Проецирующие плоскости на комплексном чертеже.
Горизонтально-проецирующей называется плоскость, перпендикулярная П1, фронтально-проецирующей – перпендикулярная П2, и профильно-проецирующей – плоскость, перпендикулярная П3. На чертеже, первая из них задана плоской фигурой (рис. 3.3а), вторая – точкой и прямой (рис. 3.3б), третья - двумя параллельными прямыми (рис. 3.3в).
3.2.3.Плоскости общего положения
Плоскостью общего положения называется плоскость, не перпендикулярная и не параллельная ни одной из плоскостей проекций, а значит, расположенная под произвольным углом к каждой из них.
У такой плоскости все проекции будут плоские фигуры (рис. 3.4). 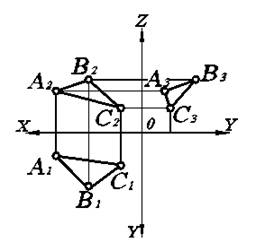
Рис. 3.4. Плоскость общего положения, заданная треугольником
3.3. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
3.4. Главные линии плоскости
Главными линиями плоскости называются линии уровня, лежащие в данной плоскости. Рассмотрим построение главных линий плоскости, заданной треугольником (рис. 3.5).
Горизонталь плоскости DАВС начинаем с вычерчивания ее фронтальной проекции h2, которая, как известно, параллельна оси ОХ. Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости DАВС, а именно, точки А и 1. Имея их фронтальные проекции А2 и 12, по линии связи получим горизонтальные проекции 11. Соединив точки А1 и 11, имеем горизонтальную проекцию h1 горизонтали плоскости DАВС. Профильная проекция h3 горизонтали плоскости DАВС будет параллельна оси ОХ по определению.
Фронталь плоскости DАВС строится аналогично (рис. 3.5) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f1, так как известно, что она параллельна оси ОХ. Профильная проекция f3 фронтали должна быть параллельна оси ОZ .
Профильная линия плоскости DАВС имеет горизонтальную р1 и фронтальную р2 проекции, параллельные осям OY и OZ, а профильную проекцию р3 можно получить по фронтальной, используя точки пересечения В и 3 с D АВС.
При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью.
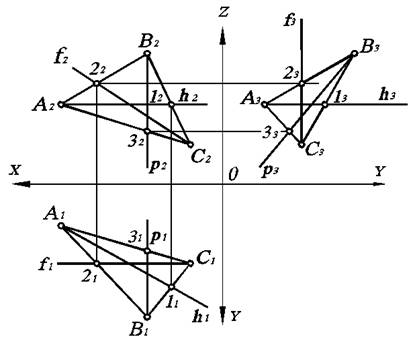
Рис. 3.5. Построение главных линий плоскости, заданной треугольником
3.5. Взаимное положение прямых и плоскостей
3.5.1. Параллельность прямых и плоскостей
а). Если прямые параллельны друг другу, тогда параллельны и их одноименные проекции. б). Прямая параллельна плоскости, если она параллельна какой - либо прямой, лежащей в этой плоскости
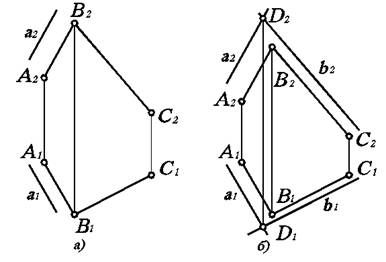
Рис. 3.6. Построение параллельно расположенных геометрических объектов.
Тогда для построения параллельной прямой а (рис. 3.6а) необходимо, чтобы обе ее проекции были параллельны одноименным проекциям прямой (например, АВ), лежащей в данной плоскости. в) Плоскости параллельны друг другу, если две пересекающиеся прямые одной плоскости попарно параллельны двум пересекающимся прямым другой плоскости. Для интерпретации этого свойства достаточно дополнить построения на рис. 3.6а еще одной прямой в, пересекающей а и параллельной ВС (рис. 3.6б).
3.5.2. Перпендикулярность прямых и плоскостей
а). Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости, одна из которых фронталь, а другая горизонталь.
Хотя для перпендикулярности вполне достаточно, чтобы указанными пересекающимися прямыми были любые прямые в данной плоскости, однако только горизонталь и фронталь позволяют получить без искажений проекции прямого угла, образованного перпендикуляром к плоскости и фронталью (на П2) и перпендикуляром к плоскости и горизонталью (на П1). Тогда очевидно, что горизонтальная проекция этого перпендикуляра расположена под прямым углом к горизонтальной проекции горизонтали, а фронтальная проекция - под прямым углом к фронтальной проекции фронтали.
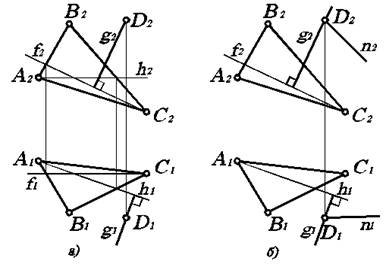
Рис. 3.7. Построение перпендикулярно расположенных геометрических объектов.
б). Плоскости перпендикулярны друг к другу, если одна из них содержит перпендикуляр к другой.
Обратимся к рис. 3.7а, где перпендикуляр g к плоскости уже построен, необходимо через точку D провести произвольную прямую q (рис. 3.7б).
3.6. Позиционные задачи на плоскости
Позиционными называются задачи на определение каких-либо общих элементов геометрических объектов, например, точки пересечения прямой и плоскости, линии пересечения двух плоскостей.
3.6.1. Пересечение прямой и плоскости
Задачу на пересечение прямой и плоскости можно решать с помощью вспомогательной секущей плоскости, которая должна удовлетворять следующим условиям:
а) быть плоскостью частного положения, так как именно плоскость частного положения проецируется на соответствующую плоскость проекций в виде прямой;
б) проходить через прямую, точку пересечения которой с плоскостью мы отыскиваем.
Рассмотрим сначала частный случай. Пусть плоскость занимает частное положение в пространстве, например, является горизонтально - проецирующей и задана треугольником АВС (рис. 3.8 а). Необходимо найти точку пересечения ее с прямой а, заданной произвольно. Поскольку на П1 горизонтально–проецирующая плоскость вырождается в прямую S1, то горизонтальной проекцией точки пересечения будет К1. Далее по линии связи на прямой а2 (очевидно точка пересечения К принадлежит прямой а) найдем фронтальную проекцию К2 точки пересечения.
Осталось определить видимые участки прямой а, поскольку на П2 часть указанной прямой будет закрыта от наблюдателя плоскостью DАВС. Для этого необходимо рассмотреть точку, где пересекаются фронтальные проекции а и какой-либо прямой ( например, АС ), лежащей в плоскости DАВС. Обозначим эту точку 12. Но пересекаться прямая а и DАВС могут только в одной точке, которую мы отыскали (К2). Все остальные точки будут точками, где они скрещиваются. Следовательно, прямая а и АС скрещиваются в пространстве. Значит, все точки, где пересекаются их проекции, будут конкурирующими, а именно 12=22. Тогда на П1 имеем по линии связи 11ÎА1С1 и 21 Î а1. Видимой является точка 2, которая принадлежит прямой а. Это сохраняется до точки пересечения К2. Затем, естественно, участок прямой а будет невидим (обозначается пунктирной линией) до выхода из-под плоскости DАВС. Теперь задачу можно считать полностью решенной.
Рассмотрим общий случай пересечения прямой и плоскости, когда обе они занимают общее положение в пространстве. Пусть плоскость задана треугольником DАВС. Здесь и в дальнейшем используем задание плоскости в основном треугольником, так как в этом случае решение задачи наиболее наглядно. Необходимо найти точку пересечения произвольно заданной прямой в с DАВС (рис. 3.8, б).
Как указано выше, нужно через прямую в провести плоскость частного положения (например, фронтально-проецирующую). Линия пересечения этой плоскости совпадает с прямой в на П2, т.е. S2=в2 . Тогда по точкам пересечения 32 и 42 построим точки 31 и 41, а следовательно, и прямую 3141, являющуюся горизонтальной проекцией линии пересечения плоскости S и DАВС. Но так как прямая 34ÌDАВС, то точка К1 будет горизонтальной проекцией точки пересечения прямой в и DАВС. По ней найдем и фронтальную проекцию К2, которая, очевидно, должна быть расположена на в2 (ведь точка пересечения принадлежит и прямой в и D АВС ).
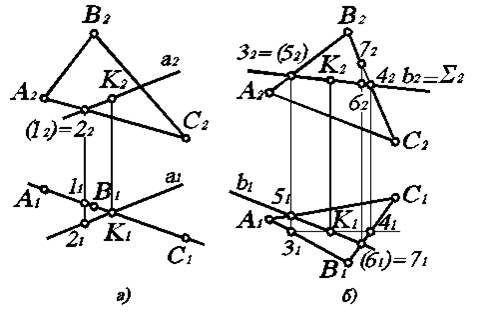
Рис. 3.8. Пересечение прямой и плоскости
Определим видимые участки прямой в на обеих проекциях по конкурирующим точкам. Для определения видимости на П2 используем фронтально-конкурирующие точки (например, точки 32=52, где скрещиваются в2 и А2В2). Очевидно, что точка 31 ближе к нам, чем точка 51. Следовательно, на П2 выше 32, тогда в этой точке А2 В2 выше, а в2 лежит под ней. Это верно только до точки пересечения К2. Далее, естественно, выше будет в2. Аналогично по горизонтально–конкурирующим точкам (например, 61=71) определяем, что в точках 61=71 прямая В1С1 лежит выше, чем в1, так как точка 72 расположена выше, чем точка 62. Невидимый участок прямой в обозначаем пунктирной линией.
3.6.2.
