Серия 7. Много текста и всё без картинок.

1. На день рождения Алёши мама испекла три вкусных торта. Каждый торт состоял из некоторого количества коржей, между которыми находился слой клубничного или вишнёвого крема. Алёша заметил, что всего на приготовление ушло 20 коржей, и 10 кремовых слоёв были клубничными. Сколько мама сделала вишнёвых слоёв крема?

2. Три коржика тяжелее пяти пирожков. Могут ли пять коржиков быть легче семи пирожков?

3. В комнате находятся 12 человек. Некоторые из них всегда лгут, а остальные всегда говорят правду. Один из них сказал: «Здесь нет ни одного честного человека», второй: «Здесь не более одного честного человека», третий: «Здесь не более двух честных людей», и т.д., двенадцатый: «Здесь не более одиннадцати честных людей». Сколько в комнате честных людей?

4. В роте 100 человек. Каждую ночь дежурят трое. Можно ли так организовать дежурство, чтобы через некое время каждый единожды подежурил с каждым?

5. Докажите, что среди чисел, меньших 10000, поровну чисел с суммой цифр 15 и с суммой цифр 21.

6. Дано шестизначное число 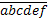, причем 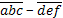делится на 7. Докажите, что само число делится на 7.

7. Можно ли в клетках таблицы 8 × 8 расставить числа от 1 до 64 так, чтобы разность между числами в соседних по стороне клетках была не более 4?

Серия 8. Зато с картинкой.

1.Три коржика тяжелее пяти пирожков. Могут ли семь коржиков быть легче тринадцати пирожков?

2.Можно ли придумать пять таких слов, чтобы каждое имело хотя бы одну общую букву ровно с тремя другими.

3. 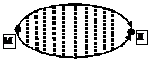Из Манчестера в Ливерпуль ведут два шоссе с односторонним движением, пересеченные десятью проселками (см. рис.). Машина выезжает из М в Л по одному из шоссе и, доезжая до любой развилки, может либо свернуть на проселок, либо не сворачивать. Свернув, она проезжает проселок до конца и продолжает путь по другому шоссе (по тем же правилам). Сколькими разными способами можно проехать из Манчестера в Ливерпуль?

4.Математическая черепаха сидит в левом нижнем углу прямоугольника 3´n. Докажите, что количество способов добраться до правой верхней клетки равно количеству способов записать в строчку 2 единицы и n–1 нуль.

5.Фокусник кладет перед зрителем колоду из n карт, и просит его посмотреть и запомнить одну карту. После этого фокусник раскладывает все карты в 6 стопок, и просит зрителя сказать, в какой из них лежит загаданная карта. Затем фокусник тасует карты, опять раскладывает их в 6 стопок, и просит зрителя назвать ту из стопок, в которой на этот раз лежит задуманная карта. Едва услышав ответ, фокусник сразу вытаскивает загаданную карту из стопки. Для какого наибольшего n можно с успехом показывать такой фокус?

6.Какое наибольшее количество натуральных чисел, не превышающих 100, можно выбрать так, чтобы ни одно из них не делилось на другое?

7.Даша и Саша играют в игру. Саша выбирает число n и на доске магическим образом появляются числа от 1 до n. За это Саша уступает Даше первый ход. За один ход разрешается вычеркнуть любое число вместе со всеми его делителями. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?