Серия первая. По мотивам матбоя.

Серия первая. По мотивам матбоя.

1.Существуют ли такие два натуральных числа, наибольший общий делитель которых равен 110, а наименьшее общее кратное равно 2000?

2.Для участников математического боя и членов жюри было приготовлено конфет столько же, сколько булочек и стаканов чая вместе. Каждый школьник съел по конфете и выпил по стакану чая, после чего осталось стаканов чая и конфет вместе столько, сколько булочек. Найдется ли стакан чая для заглянувшего к ним члена жюри?

3.Мимо наблюдателя по дороге Кострома - Иваново проехали с равными между собой промежутками времени автобус, мотоцикл и автомобиль. Мимо другого наблюдателя они проехали с такими же промежутками, но в другом порядке: автобус, автомобиль, мотоцикл. Найдите скорость автобуса, если скорость автомобиля 60 км/ч, а мотоцикла - 30 км/ч.

4.Незнайка отметил на плоскости 15 точек и утверждает, что какое бы натуральное число от 1 до 7 ему не назвали, он может указать прямую, на которой лежит ровно столько отмеченных точек. Прав ли он?

5.На витрине ювелирного магазина лежат 9 золотых монет весом 100г, 101г, ..., 108г. Рядом с каждой монетой лежала этикетка, указывающая вес монеты. Первого апреля шутник переложил этикетки. Продавец точно знает, какая монета сколько весит. За какое наименьшее число взвешиваний на чашечных весах со стрелкой, показывающей разность весов на чашках, он сможет показать хозяину, который не знает, какая монета сколько весит, как правильно положить этикетки?

6.Фунтик-Шпунтик развлекается тем, что выписывает все натуральные числа, цифры которых убывают, а затем в каждом вставляет знаки сложения и вычитания между соседними цифрами по порядку “–”, “+”, “–”, “+”, ... и считает результат. (Например, 97641 превращается в 9–7+6–4+1=5.) В конце он все результаты сложил. Какое число получено?

Серия 4. Очень-очень маленькая.

1.Таня стоит на берегу речки. У неё есть два глиняных кувшина: один – на 5 литров, а про второй Таня помнит лишь то, что он вмещает то ли 3, то ли 4 литра. Помогите Тане определить ёмкость второго кувшина.

2. В каждой клетке бесконечного клетчатого поля написано по натуральному числу. Докажите, что найдется число, не превосходящее всех своих соседей.

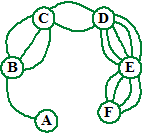
3.На рисунке показана схема расположения тропинок и полянок (A, B, C, D, E и F) в Дремучем лесу. а)Сколько существует способов попасть с полянки А на полянку F, побывав на полянках B, С, D и Е по одному разу?
б) Жители Дремучего леса собрались протоптать еще одну тропинку так, чтобы способов стало 132. Между какими полянками следует протоптать эту тропинку?

4.На доске размером 9×9 клеток закрашены в черный цвет первый, третий, пятый, седьмой и девятый столбцы. Вася хочет расположить на этой доске Т-тетраминошку. Каких способово у него больше: тех, в которых в фигурке окажется 3 черных клетки, или тех, в которых одна?

Серия 6. О голодной козе.

Козы прожорливы и съедают все, до чего могут дотянуться. Поэтому коз держат на привязи.

1.Нарисуйте участок луга, который выест коза, привязанная двумя веревками длиной 2 м каждая к двум одиноко стоящим колышкам, находящимся друг от друга на расстоянии: а) 2 метра; б) 4 метра.

2. 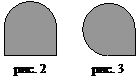Привязывать козу можно либо к колышкам, либо к горизонтальной палке. Как привязать с помощью веревок козу так, чтобы она съела всю траву на участке в форме:
а) полукруга;
б) сектора;
в) прямоугольника;
г) фигуры, изображенной на рисунке 2;
д) фигуры, изображенной на рисунке 3;
е) правильного треугольника;
ж) правильного шестиугольника.

3. 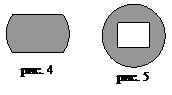Коза привязана к одиноко стоящему на лугу колышку. Введём дополнительно в действие собаку, которую будем привязывать к колышкам или к горизонтальным палкам, и она будет мешать козе есть. Как этой собакой удержать козу:
а) в кольце?
б) в полукруге?
в) в фигуре, изображенной на рис.4?
г) в фигуре, изображенной на рис.5?

4.Удержите непривязанную козу с помощью одной собаки в треугольнике.

5.а) Один конец шеста длиной 4 метра прикреплен к столбу и свободно вокруг него вращается. К другому концу шеста веревкой длиной 1 метр привязана коза. Какую фигуру выест коза? А если веревка имеет длину 5 метров?
б) А если веревку заменить шестом соответствующей длины?

Серия 8. Зато с картинкой.

1.Три коржика тяжелее пяти пирожков. Могут ли семь коржиков быть легче тринадцати пирожков?

2.Можно ли придумать пять таких слов, чтобы каждое имело хотя бы одну общую букву ровно с тремя другими.

3. 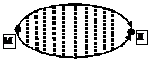Из Манчестера в Ливерпуль ведут два шоссе с односторонним движением, пересеченные десятью проселками (см. рис.). Машина выезжает из М в Л по одному из шоссе и, доезжая до любой развилки, может либо свернуть на проселок, либо не сворачивать. Свернув, она проезжает проселок до конца и продолжает путь по другому шоссе (по тем же правилам). Сколькими разными способами можно проехать из Манчестера в Ливерпуль?

4.Математическая черепаха сидит в левом нижнем углу прямоугольника 3´n. Докажите, что количество способов добраться до правой верхней клетки равно количеству способов записать в строчку 2 единицы и n–1 нуль.

5.Фокусник кладет перед зрителем колоду из n карт, и просит его посмотреть и запомнить одну карту. После этого фокусник раскладывает все карты в 6 стопок, и просит зрителя сказать, в какой из них лежит загаданная карта. Затем фокусник тасует карты, опять раскладывает их в 6 стопок, и просит зрителя назвать ту из стопок, в которой на этот раз лежит задуманная карта. Едва услышав ответ, фокусник сразу вытаскивает загаданную карту из стопки. Для какого наибольшего n можно с успехом показывать такой фокус?

6.Какое наибольшее количество натуральных чисел, не превышающих 100, можно выбрать так, чтобы ни одно из них не делилось на другое?

7.Даша и Саша играют в игру. Саша выбирает число n и на доске магическим образом появляются числа от 1 до n. За это Саша уступает Даше первый ход. За один ход разрешается вычеркнуть любое число вместе со всеми его делителями. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Серия 10. Двузначная

1. Четыре страны имеют форму треугольников. Нарисуйте, как могли быть расположены друг относительно друга страны, если у каждой из них есть общие границы (по отрезку) с тремя другими.

2. Двое мальчиков катались на лодке. К берегу подошел отряд солдат. Лодка так мала, что на ней могли переправиться двое мальчиков или только один солдат. Смогут ли солдаты переправиться через реку?

3. Серый Волк позвонил на Бейкер-стрит и заявил, что у него украли очень ценную вставную челюсть, инкрустированную бриллиантами. Подозреваемые — Ниф-Ниф, Наф-Наф и Нуф-Нуф. Известно, что:

а)каждый из троих подозреваемых в день кражи побывал в гостях у волка, и никто больше к нему не заходил;

б) если Ниф-Ниф виновен, то у него был ровно один сообщник;

в)если Нуф-Нуф не виновен, то не виновен также и Наф-Наф;

г) если Наф-Наф не виновен, то не виновен также и Нуф-Нуф;

д) если виновны двое, то Ниф-Ниф один из них.

Кому Шерлок Холмс предъявит обвинение?

4. Длину прямоугольника уменьшили на 10%, а ширину уменьшили на 20%. При этом периметр прямоугольника уменьшился на 12%. На сколько процентов уменьшится периметр прямоугольника, если его длину уменьшить на 20%, а ширину уменьшить на 10%?

5. В припортовой таверне пираты Боб и Иван состязались в изготовлении и употреблении крепких напитков. Боб изготовил коктейль из рома и виски, а Иван смешал водку с портвейном. Известно, что ром крепче водки, а виски крепче портвейна. Может ли смесь Ивана оказаться крепче коктейля Боба?

6. Сколькими способами можно выбрать из чисел от 1 до 100 три числа так, чтобы их сумма делилась на 3?

7. Играют трое. На столе лежат 2010 кучек конфет, по 100 штук в каждой. За ход разрешается взять произвольное количество конфет из одной кучи. Ходы делаются по очереди: Даша – Соня – Юля – Даша – Соня – Юля и т.д. Проигрывает тот, кто не может сделать ход. Могут ли Соня и Юля, объединившись, довести Дашу до проигрыша?

Серия 12. Зверинец.

1. Доктор Айболит раздал четырём заболевшим 1234 чудодейственные таблетки. Кощей получил на одну таблетку больше, чем кикимора, Баба Яга на одну больше, чем Кощей, а Змей Горыныч – на одну больше, чем Баба Яга. Сколько таблеток придётся съесть Змею Горынычу?

2. Расшифруйте ребус: Б + БЕЕЕ = МУУУ

3. В квадратном ковре со стороной 1 м моль проела 51 точечную дырку. Докажите, что некоторой квадратной заплаткой стороной 20 см можно закрыть не менее трёх дырок.

4. На бесконечной в обе стороны клетчатой ленте сидит кузнечик, который умеет прыгать на 7 клеток вправо и на 4 клетки влево. Докажите, что он сможет добраться до любой клетки.

5. Однажды профессор консерватории пригласил к себе в гости музыкантов Мартышку, Козла, Осла и Косолапого Мишку. В комнате у профессора вокруг стола стоит несколько стульев. Профессор насчитал 120 способов рассадить на них своих гостей. После этого он решил подсчитать, в скольких способах Мартышка и Мишка сидят на соседних стульях, и насчитал 60 способов. Потом он решил подсчитать, а в скольких способах Козел и Осел не сидят рядом. И насчитал 40 способов. Докажите, что профессор где-то ошибся.

6. Перед Белкой шоколадка размера а) 8×8 б) 5×6 долек. В одной из долек спрятан орех. Белка может указать на любую прямоугольную часть и узнать, находится ли в ней орех. Какого наименьшего количества вопросов ей хватит, чтобы найти орех?

7. На клетчатой бумаге отметили 100 клеток. Докажите, что из них можно выбрать 50 так, чтобы среди выбранных клеток не было соседних по стороне.

Серия 13, начало.

1.

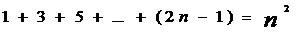
а) Докажите это с помощью индукции.

б) Докажите это с помощью геометрии.

2. В конференции участвовали 19 ученых. После конференции каждый из них отправил 2 или 4 письма участникам этой конференции. Могло ли получиться так, что каждый участник получил по 3 письма?

3. Количество интегралов, взятых Марией Михайловной, выражается трехзначным числом, начинающимся на 9. Если первую цифру этого числа перенести в конец, то получим количество интегралов, взятых Анной Михайловной. Известно, что Анна Михайловна взяла на 90 интегралов меньше. Выразите их мучения численно.

Серия 13, продолжение.

1. На какое минимальное количество прямоугольников можно разрезать следующую фигуру:
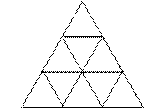2. Правильный треугольник разбит прямыми, параллельными сторонам, на 9 равных правильных треугольников. Петя отметил один из входящих в него треугольников невидимыми чернилами. Вася может указать любой треугольник со сторонами, идущими по линиям разбиения, и Петя скажет ему, лежит ли отмеченный треугольник в указанном. За какое наименьшее число таких вопросов Вася наверняка сможет найти отмеченный треугольник?
3. Вражеская шпионская сеть устроена следующим образом. Каждый из шпионов знает ровно четырех других. Получив какую-либо информацию шпион передает ее всем другим, известным ему, шпионам. Однажды, при передаче одного важного сообщения все шпионы сработали безукоризненно, кроме Васи, который не смог связаться со своим знакомым шпионом Петей. Докажите, что, несмотря на это вся сеть будет оповещена.
4. Все рыцари и лжецы острова построились по кругу, и каждый сказал, про соседа справа – рыцарь он или лжец. На основании этой информации, путешественник смог сообразить, какова доля рыцарей в населении. А чему она равна?

Серия 14. Жужжащая.

1. Максим должен был разделить число на 2, а к результату прибавить 3, а он, по ошибке, умножил число на 2, а от полученного произведения отнял 3. Ответ все равно получился правильный. Какой?

2. Артем и Саша вместе знают столько же плохих слов, сколько Игорь и Дима. А Артем с Димой знают таких слов больше, чем Саша с Игорем. Расположите юных лингвистов по количеству известных им плохих слов, если известно, что Саша знает их больше, чем Артем и Игорь вместе взятые.

3. В квадратном ковре со стороной 1 м моль проела 15 точечных дырок. Докажите, что из него можно вырезать неповрежденный круг радиуса 12,5 см.

4. На шестиугольной решетке (см. рисунок) пчёлы сложили мед в 300 шестиугольников. Докажите, что из них можно выбрать 100 так, чтобы не было соседних по стороне.

5. Выразите без многоточий число 1+2+4+…+2¹⁰⁰.

6. На клетчатой бумаге построены несколько прямоугольников со сторонами, параллельными линиям сетки и общим центром О в одном из узлов сетки. За один вопрос можно про любой из узлов узнать, у скольких прямоугольников он лежит внутри. Как за четыре вопроса узнать, сколько прямоугольников содержат только один узел О?

7. Есть n одинаковых банок. Из них n-1 доверху заполнены красками разных цветов, а последняя пустая. Разрешается переливать из любой банки в любую произвольное количество краски. Докажите, что можно сделать так что каждая из n банок будут заполнены поровну равномерной смесью всех красок.

Олипиада ЮМШ 6 класса 5. Есть доска 9×9 клеток. В каждую клетку поставили число 0, 1 или 2 так, чтобы в каждом квадратике 2×2 сумма была больше четырёх. Докажите, что сумма всех чисел на доске не меньше 89.6. Мама выдала Ванечке двузначное число. Ванечка сложил в столбик это число с ним же, после чего проделал то же самое с полученным результатом, и так 11 раз. Когда мама стала проверять его вычисления, выяснилось, что Ванечка при сложении двойки с двойкой получал всегда вместо четырёх пять (или шесть, если там был ещё перенос). В итоге у него получилось число, которое оканчивается ровно на один ноль. Каким могло быть исходное число?7. Круг разбит на 100 секторов. Мирза и Егор по очереди заполняют сектора (в произвольном порядке) натуральными числами (первым ходит Мирза). Когда все сектора заполнены, Мирза пишет на доску ещё одно натуральное число, после чего Егор режет круг на две половинки (по 50 секторов). Если сумма чисел в одной из них оканчивается на те же две цифры, что и число на доске, то побеждает Егор, иначе побеждает Мирза. Кто победит при правильной игре?

15 серия: Начало.

1. Диана, Кирилл и Афанасий задумали по трехзначному числу. Могло ли так оказаться, что сумма числа Афанасия с числом Дианы равна 600, а сумма числа Кирилла с числом Дианы равна 1500?

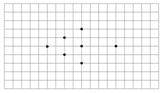
2. На клетчатой бумаге поставлено 7 точек так, как показано на рисунке. Перечеркните все эти точки тремя отрезками, не отрывая карандаша от бумаги. Отрезки не обязательно должны проходить по линиям сетки.

3. На математический кружок пришли три длинноволосых ребёнка. Их фамилии - Кубанец, Чиковани и Никитина, имена - Саша, Женя и Дима. Учитель знает об этом, но на взгляд не может определить, кто из них мальчик, а кто девочка. Каждый из детей назвал своё имя и фамилию, причём учителю известно, что мальчики называют и то и другое неверно, а девочки правильно. Может ли учитель гарантированно определить по ответам детей, сколько среди них мальчиков? (Кубанец и Чиковани могут быть как мальчиками, так и девочками, Саша и Женя тоже).

4. В куче лежит N камней, N>3. Двое играют в игру. Первый игрок забирает из кучи один камень. Каждым следующим ходом можно забрать либо ровно на один камень больше, либо ровно на один меньше, чем только что взял соперник, но не менее одного камня. Проигрывает тот, кто не может сделать очередной ход. Кто из игроков может выиграть, как бы ни играл его соперник?

Серия первая. По мотивам матбоя.

1.Существуют ли такие два натуральных числа, наибольший общий делитель которых равен 110, а наименьшее общее кратное равно 2000?

2.Для участников математического боя и членов жюри было приготовлено конфет столько же, сколько булочек и стаканов чая вместе. Каждый школьник съел по конфете и выпил по стакану чая, после чего осталось стаканов чая и конфет вместе столько, сколько булочек. Найдется ли стакан чая для заглянувшего к ним члена жюри?

3.Мимо наблюдателя по дороге Кострома - Иваново проехали с равными между собой промежутками времени автобус, мотоцикл и автомобиль. Мимо другого наблюдателя они проехали с такими же промежутками, но в другом порядке: автобус, автомобиль, мотоцикл. Найдите скорость автобуса, если скорость автомобиля 60 км/ч, а мотоцикла - 30 км/ч.

4.Незнайка отметил на плоскости 15 точек и утверждает, что какое бы натуральное число от 1 до 7 ему не назвали, он может указать прямую, на которой лежит ровно столько отмеченных точек. Прав ли он?

5.На витрине ювелирного магазина лежат 9 золотых монет весом 100г, 101г, ..., 108г. Рядом с каждой монетой лежала этикетка, указывающая вес монеты. Первого апреля шутник переложил этикетки. Продавец точно знает, какая монета сколько весит. За какое наименьшее число взвешиваний на чашечных весах со стрелкой, показывающей разность весов на чашках, он сможет показать хозяину, который не знает, какая монета сколько весит, как правильно положить этикетки?

6.Фунтик-Шпунтик развлекается тем, что выписывает все натуральные числа, цифры которых убывают, а затем в каждом вставляет знаки сложения и вычитания между соседними цифрами по порядку “–”, “+”, “–”, “+”, ... и считает результат. (Например, 97641 превращается в 9–7+6–4+1=5.) В конце он все результаты сложил. Какое число получено?