Тема 2. Комплексный чертеж прямой линии

8. Построить профильную проекцию отрезка АВ (рис. 12, а).

а б

Рис. 12

8.1. Показываем линии связи для профильной и фронтальной проекций (см. задачу 1 п. 1.3), рис. 12, б.

8.2. На профильной плоскости проекций показываем проекцию наиболее удаленной точки (предварительно определив положение точек А и В на горизонтальной плоскости проекций, см. задача 6). Теперь все дальнейшие построения будут производиться правее этой точки.

8.3. На горизонтальной проекции определяем разность координат вдоль оси Y – DY. (см. задачу 7)

8.4. Откладываем DY от профильной проекции точки В₃ вправо вдоль линии связи и показываем профильную проекцию точки В (В₃).

8.5. Соединяем полученные проекции и получаем третью проекцию [АВ].

8, а. Построить профильную проекцию отрезка АВ, горизонтальную проекцию CD и фронтальную проекцию отрезка EF (рис. 13).

Рис. 13

9. Определить натуральную величину отрезка АВ (рис. 14, а) и углы наклона его к плоскостям проекций. Применить правило прямоугольного треугольника.

а б

Рис. 14

9.1. Проводим линию, перпендикулярную к одной из проекций отрезка АВ. Перпендикуляр опускаем из проекции любой точки (А или В), рис. 14, б.

9.2. Откладываем на перпендикуляре отрезок равный разности расстоя-ний от точек отрезка до соответствующей плоскости проекций: – Dx (до П₃), Dy (до П₂) или Dz (до П₁) – (разности координат точек вдоль оси перпендикулярной к плоскости проекций, на которой строится прямоугольный треугольник).

9.3. Строим прямоугольный треугольник, один катет которого будет проекция отрезка, а второй катет – разность координат. Длина гипотенузы будет равна натуральной величине отрезка (правило прямоугольного треугольника)[29].

9.4. Угол, противолежащий катету разности координат, будет углом наклона к соответствующей плоскости проекций: a – угол наклона к горизонтальной плоскости проекций; b – угол наклона к фронтальной плоскости проекций; g – угол наклона к профильной плоскости проекций.

9.5. При построении прямоугольного треугольника для определения угла наклона к плоскости П₃ необходимо построить профильную проекцию отрезка (см. задачу 7).

9, а. Определить натуральную величину отрезка АВ (рис. 15) и углы наклона его к плоскостям проекций. Воспользоваться правилом прямоугольного треугольника.

Рис. 15

10. Построить прямоугольную изометрическую проекцию заданной горизонтали [30](рис. 16). Определить по изометрической проекции углы наклона горизонтали к плоскостям проекций и показать их на эпюр. Записать свойства горизонтальной прямой уровня (длина проекций в сравнении с натуральной величиной, углы наклона к плоскостям проекций, положение относительно координатных осей).

Рис. 16

10.1. Для построения изометрической проекции горизонтали необходимо указать еще одну точку В, принадлежащую прямой h.

Систему координат на эпюр проводим самостоятельно.

Свойства горизонтали: hIIП₁; Ih₁I=IhI; a=0; h₂IIX Ù ^Z; h₃IIY Ù ^ z.

11. Построить прямоугольную изометрическую проекцию заданной фронтали[31] (рис. 17). Показать углы наклона фронтали к плоскостям проекций. Определить натуральную величину.

Свойства фронтали: fIIП₂; If₂I=IfI; b=0; f₁IIX Ù ^ Y; f₃IIZ Ù ^ Y.

Рис. 17

12. Построить прямоугольную горизонтальную и изометрическую проекцию заданной профильной прямой уровня [31](рис. 18). Указать свойства профильной прямой уровня (длина проекций в сравнении с натуральной величиной, углы наклона к плоскостям проекций, положение относительно координатных осей).

12.1. Проводим линию связи А₂–А₁ (задача 1, п., 1.3), на которой указываем положение горизонтальной проекции точки А.

12.2. Произвольно выберем профильную проекции точки В (В₃). Остальные две проекции находим по правилам построения трех проекций (см задачи 7, 8)

12.3. Свойства профильной прямой уровня: pIIП₃; Ip₃I=IpI; g=0; p₁IIY и ^X; p₂IIZ и ^ X.

Рис. 18

13. Достроить проекции отрезков. Определить углы a, b, g горизонтальной прямой АВ = 50 мм (рис. 19, а), профильной прямой CD = 30 мм (рис. 19, б).

аб

Рис. 19

13.1. Строим недостающие проекции прямой (см. задачи 10, 11).

13.2. Строим проекции отрезка АВ (рис. 20, а. Воспользуемся свойствами горизонтали: h₂ 2 x (через точку А₂ проводим прямую) и Ih₁I=IhI (на горизонтальной проекции откладываем отрезок IА₁В₁I=IАВI=50 мм); задача – рис. 20, б: согласно свойству профильной прямой уровня – IP₃I=IPI откладываем на профильной проекции отрезок ICDI=IC₃D₃I=30 мм. Далее см. задачи 6, 7.

а б

Рис. 20

13, а. Через точку А провести горизонтальный отрезок АВ, а через точку С профильный отрезок, CD, имеющие угол наклона к фронтальной плоскости 30° и длину 50 мм (рис. 21).

Рис. 21

14. Построить в трех проекциях фронтальный отрезок АВ = 45 мм, наклоненного к П₃ под углом 60° (рис. 22). Положение проекций отрезка выбрать самостоятельно.

Рис. 22

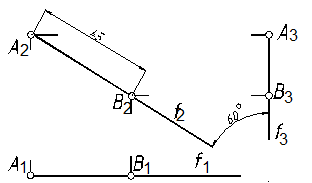14.1. Используя понятие о линиях связи (см. задачу 1, п. 1.3), показываем положение проекций точки А:, А₁, А₂ и А₃.(рис. 23).

14. 2. Далее см. задачу 12.

Рис. 23

14, а. Построить в трех проекциях фронтальный отрезок АВ = 50 мм, наклоненный к П₁ под углом 60° (рис. 24). Положение проекций отрезка выбрать самостоятельно.

Рис. 24

15. На отрезке АВ (рис. 25) определить точку С так, чтобы АС:СВ = 3:5. Задачу решить двумя способами.

15.1. Первый способ [13] (рис. 25, а): проведем через любую проекцию точки (А или В) линию под углом, отличным от 0 или 180°, на которой отложим (при помощи циркуля или линейки) восемь равных частей. Далее проводим линию через точку третьего отрезка (от точки А), параллельную линии, соединяющей конец последнего отрезка с проекцией второй точки. Точка пересечения первой линии будет проекцией точки С. Выполнив аналогичные построения для второй проекции отрезка, получим вторую проекцию точки С.

15.2. Второй способ (рис. 25, б): строим профильную проекцию отрезка АВ (задачу 7) и аналогично первому способу находим профильную проекцию точки С. Далее определяем горизонтальную и фронтальную проекции точки С (задачу 7).

а б

Рис. 25

15, а. Разделить графически отрезок СD в отношении 2:4(рис. 26).

Рис. 26

16. На прямой m определить точку С, удаленную от точки А на 30 мм (рис. 27, а).

а б

Рис. 27

16.1. Для решения задачи построим произвольно профильную проекцию прямой m (рис. 27, б), на которой отложим 30 мм. Далее см. задачу 13.

16, а. На прямой m определить точку С, удаленную от точки А на 30 мм (рис. 28). Построить горизонтальную проекцию.

Рис. 28

17 . На прямой m определить точку С удаленную от точки А на 30 мм (рис. 29, а).

17.1. Для решения задачи отметим на прямой m проекции промежуточной точки В (рис. 29, б) и определим натуральную величину АВ (см. задача 9), на линии которой отложим натуральную величину АС, по которой определим фронтальную и по линиям связи (см. задачу 1 п. 1.3) горизонтальную проекции точки С.

а б

Рис. 29

17, а. На прямой m определить точку, С удаленную от точки А на 30 мм (рис. 30).

Рис. 30

18. Определить недостающие проекции точек К и L (см. задачи 6, 10, 13), принадлежащих горизонтали АВ.

18.1. Первый способ (рис. 32, а) основан на построении третьей проекции отрезка (см. задачу 8).

18.2. Второй способ (рис. 32, б) основан на построении пропорциональных отрезков пу-тем построения подобных треу-гольников [13] (см. задачу 15).

Рис. 32

18, а. Определить недостающие проекции точек К и L (рис. 33)

Рис. 33

19. На прямоугольной изометрической проекции (рис. 34, а) показана горизонтально проецирующая прямая а. Показать ее проекции. Построить эпюр этой прямой (рис. 34, б). Записать свойства горизонтальной проецирующей прямой (длина, углы наклона к плоскостям проекций, положение относительно координатных осей).

19.1. Выбираем произвольно две точки на этой прямой и находим их проекции (см. задачу 1). Далее соединяем указанные точки соответствующих проекций и получаем проекции горизонтально проецирующей прямой.

а б

Рис. 34

19.2. Так как горизонтально проецирующая прямая перпендикулярна горизонтальной плоскости проекций, то угол этой прямой с горизонтальной плоскостью будет равен 90°. Относительно фронтальной и профильной плоскости проекций эта прямая будет располагаться параллельно, а значит, и угол между этой прямой и плоскостями будет равен 0 или 180° (рис. 35, а).

19.3. На эпюр (рис. 35, б) строим горизонтальную проекцию прямой (как проекцию точки А или В). Линии связи (см. п. 1.3.) горизонтальной и фронтальной проекции этих точек совпадут с фронтальной проекцией прямой. Профильная проекция будет параллельна оси z и иметь координату Y точки А или В.

19.4. Свойства: а2П₂ и П₃ и, перпендикулярна к П₁. a =90°, bÙg=0Ú180°, , .

а б

Рис. 35

19, а. Построить три проекции горизонтально проецирующего отрезка длиной 25 мм (рис. 36).

Рис. 36

20. На прямоугольной изометрической проекции (рис. 37, а) заданной фронтально проецирующей прямой а показать ее проекции. Построить эпюр этой прямой (37, б). Записать свойства горизонтальной прямой уровня (длина, углы наклона к плоскостям проекций, положение относительно координатных осей).

а б

Рис. 37

20.1. Выбираем произвольно две точки на прямой а (рис. 38, а) и находим их проекции (см. зад. 1). Далее соединяем указанные точки, соответствующих проекций и получаем проекции фронтально проецирующей прямой.

20.2. Так как фронтально проецирующая прямая перпендикулярна фронтальной плоскости проекций, то угол этой прямой с фронтальной плоскостью будет равен 90°. Относительно горизонтальной и профильной плоскости проекций эта прямая будет располагаться параллельно, а значит, и угол между этой прямой и плоскостями будет равен 0 или 180°.

а б

Рис. 38

20.3. На эпюр (рис. 38, б) строим проекции прямой (как проекцию точки А или В). Линия связи (см., задачу 1 п. 1.3.) фронтальной, горизонтальной и профильной проекций этих точек совпадут с горизонтальной и профильной проекцией прямой.

20.4. Свойства: а2 П₁ и П₃ и перпендикулярна к П₂. b = 90°, aÙg = 0 Ú 180°, , .

20, а. Построить три проекции фронтально проецирующего отрезка длиной 25 мм (рис. 39).

Рис. 39

21. На прямоугольной изометрической проекции заданной профильно проецирующей прямой показать ее проекции (рис. 40, а). Построить эпюр этой прямой (рис. 40, б). Записать свойства горизонтальной прямой уровня (длина, углы наклона к плоскостям проекций, положение относительно координатных осей).

а б

Рис. 40

21.1. Выбираем произвольно точку А (рис. 41, a) на прямой а и находим её проекцию (см. задача 1). Вторая точка В лежит в плоскости П₃ (точка пересечения прямой с профильной плоскостью). Далее соединяем указанные точки соответствующих проекций и получаем проекции профильно проецирующей прямой.

21.2. Так как профильно проецирующая прямая перпендикулярна профильной плоскости проекций, то угол этой прямой с этой плоскостью будет равен 90°. Относительно горизонтальной и профильной плоскости проекций эта прямая будет располагаться параллельно, а значит, и угол между этой прямой и плоскостями будет равен 0 или 180°.

21.3. На эпюр (рис. 41, б) строим проекции прямой (как проекцию точки А или В). Линии связи (см. задачу 1 п. 1.3.) фронтальной и профильной проекций этих точек совпадут с фронтальной и профильной проекцией прямой.

а б

Рис. 41

21.4. Свойства: а2П₁ и П₂ и перпендикулярна к П₃,. g = 90°, b Ù a = 0 Ú 180°, , .

21, а. Построить три проекции профильно проецирующего отрезка длиной 25 мм.

Контрольные вопросы

1. Изображение прямой на комплексном чертеже.

2. Как изображается прямая общего положения и как она располагается по отношению к плоскостям проекций? Показать на примере.

4. Какие существуют прямые частного положения?

5. Прямые уровня и их свойства, изображение на комплексном чертеже.

6. Проецирующие прямые, их свойства.

7. Определение натуральной величины прямой общего положения и углов наклона ее к плоскостям проекций методом прямоугольного треугольника.

8. Определение натуральной величины и углов наклона ее к плоскостям проекций:

а) прямой уровня

б) проецирующей прямой.