Закон природы - секрет Вселенной
Скачано с NALIVATOR.COM
Закон природы - секрет Вселенной
Р.Н.Эллиотт, 1946 г.

Титульный лист прижизненного издания книги
Оглавление
Введение Ритм в природе
I Великая пирамида в Гизе
II Закон природы
III Человеческая деятельность
IV Характерные особенности человеческой деятельности
V Коррекции
VI Удлинения
VII Вершины растянутой волновой плоскости
VIII Чередование
IX Шкалы
X Примеры
XI Тринадцатилетний треугольник
XII Прорыв
XIII Цена золота
XIV Патенты
XV Технические особенности
XVI Железнодорожный индекс Доу
XVII Значение новостей
XVIII Работа с графиками
XIX Выбор времени инвестирования
XX Выбор инструмента для инвестирования
XXI Символические цифры пирамиды
XXII Закон движения
XXIII Великая депрессия
XXIV Эмоциональные циклы отдельных личностей
XXV Пифагор
XXVI Разное
XXVII Бычий рынок 1942-1945 годов
Обзор и заключение
Принятые сокращения
(Гл) Глава. “Гл24” означает “Глава 24”
(Рис) Рисунок. “Рис4” означает “Рисунок 4”
(ОТ) Orthodox Top – ортодоксальная вершина
(Фибо) Число из последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …)
(КФибо) Коэффициенты Фибо, такие как 0.62 или обратный 1.62
Предисловие переводчика
Эта книга является венцом творения Ральфа Эллиотта, первооткрывателя Закона волн.
К началу 40-х годов прошлого века Ральф Нельсон Эллиотт завершил разработку концепции, в которой взлеты и падения человеческих эмоций и результаты человеческой деятельности следуют естественной последовательности событий, управляемой законом природы. Он соединил модели поведения человеческого общества с соотношением Фибоначчи или “золотой” пропорцией - математическим явлением, известным в течение тысячелетий математикам, естествоиспытателям, художникам, зодчим и философам в качестве вездесущего закона природы, которому подчиняется форма и движение.К 1946 году Эллиотт объединил свои работы в своей последней монографии.В конце каждой главы в разделе СНОСКИ даются комментарии Роберта Пректера. Мои небольшие пояснения и дополнения традиционно отмечены звездочкой *.
Автор перевода:
Дмитрий Возный
Глава II. Закон природы
Закон природы был известен, по крайней мере, пять тысяч лет назад. Приблизительно к 1500 году до нашей эры Египет, самое древнее из современных государств, был в расцвете своих сил. Не известно, когда были построены Египетские пирамиды. Но Великая пирамида в Гизе была спроектирована, по меньшей мере, пять тысяч лет назад. Некоторые ученые выдвигают предположение, что она существовала до угрозы всемирного потопа, который заставил Ноя построить ковчег. Другие полагают, что ей может быть тридцать тысяч лет.
В журнале Life (от 3 декабря 1945 года) появилась весьма интересная статья под названием “Строительство Великой пирамиды”. Господин Бел Геддес (Bel Geddes) подготовил примеры различных этапов строительства и представил их зарисовки. Отчет был подготовлен для энциклопедии Britannica. В нем говорится, что общий вес использованных строительных материалов составляет 3 277 000 тонн, в то время как материалы, использованные в Empire State Building, самом высоком здании в мире, весят лишь 305 000 тонн.
Изумительная изобретательность, мастерство, время и труд, затраченные проектировщиками и строителями этих пирамид на возведение вечного символа, демонстрируют величайшую значимость того послания, которое они хотели передать потомкам. То был исторический период до возникновения литературы и иероглифов, следовательно, символические цифры были единственным средством записи.
В течение веков Египетские пирамиды основательно изучили, особенно в последние годы. Но насколько я понял, египтологи пропустили важный, возможно, самый важный символ. Я говорю о внешних линиях пирамиды в Гизе.
Пифагор (Pythagoras) был прославленным греческим философом пятого века до н.э. Старые энциклопедии дают детальное описание его деятельности. Encyclopedia Britannica приводит диаграмму и загадочную надпись, которая может быть единственной записью, оставленной им. Она была сделана по возвращении его в Грецию после продолжительного путешествия в Египет. Диаграмма и надпись (Секрет Вселенной*) представлены на рисунке 1. Логично предположить, что диаграмма Пифагора относится к пирамиде.

Установлены следующие первоначальные размеры Великой пирамиды в Гизе: основание 783.3 фута, высота 484.4 фута, их соотношение 61.8%. Высота 484.4 фута равна 5813 дюймам (5-8-13 Фибо).
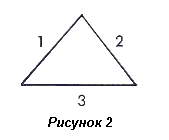
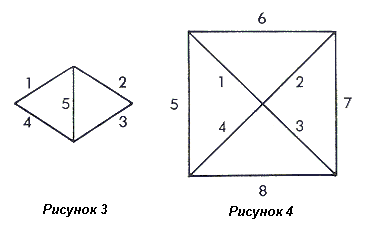
Глядя на пирамиду с одной из ее четырех сторон, видно 3 линии. Диаграмма на рисунке 2 является законченным циклом. Осматривая пирамиду с одного из ее четырех углов, видно 5 линий, как показано на рисунке 3. У пирамиды 5 поверхностей – четыре над землей и основание. Со своей вершины пирамида открывает 8 линий, как показано на рисунке 4.
Фибоначчи (Fibonacci) был итальянским математиком тринадцатого века нашей эры. В то время он был лучше известен как Леонардо Пизанский (Leonardo de Pisa). Он посетил Египет и Грецию, а по возвращении в Италию открыл то, что сейчас известно как арифметическая прогрессия (последовательность Фибоначчи*). Вот эта последовательность: 1 2 3 5 8 13 21 34 55 89 144…
Сумма любых двух соседних чисел равна следующему числу, например, 5 + 8 = 13. Любое число, разделенное на последующее, дает соотношение 0.618, например, 8 / 13 = 0.618. Любое число, разделенное на предыдущее, дает обратное значение 1.618 (соотношение чисел в начале ряда не совсем точно, но достаточно близко для практических целей). Для простоты я буду ссылаться на первое значение в виде 0.62, а на последнее как на 1.62.
Обратите внимание, что первые пять чисел последовательности Фибо 1, 2, 3, 5 и 8 присутствуют на детальной диаграмме пирамиды.
Недавно умерший Джей Хэмбидж (Jay Hambidge), американский художник, посетил Египет, Грецию и Италию и написал несколько весьма значительных и интересных книг. Я процитирую страницы 27 и 28 его книги под названием Практическое применение динамической симметрии.
“Ботаники используют цветок подсолнуха в качестве одной из общих иллюстраций закона расположения листьев. Он является феноменом особенно в двумерной форме. Семечки распределены по кругу подсолнуха в ячейках ромбовидной формы, а совокупность этих ячеек формирует узор интересных изогнутых линий, чем-то похожий на старинную резьбу на корпусе карманных часов. Эта конфигурация дугообразных линий является интересной особенностью расположения семян подсолнуха.
[Для наглядности приведу ниже фото подсолнуха из инета*]

Подсолнух.
Во-первых. Дугообразная линия сама по себе является кривой определенного вида. Собственно говоря, она в точности похожа на линию роста морской раковины. Она правильной формы и обладает определенными математическими свойствами. Эти свойства являются необходимым результатом единой формы роста, как будет сейчас показано.
Во-вторых. Если пересчитать дугообразные линии, то на обычном подсолнухе диаметром пять или шесть дюймов можно обнаружить 89 таких линий. Закручивающихся в одну сторону – 55 линий, а закручивающихся в другую сторону – 34. То есть, обычный цветок демонстрирует 55 линий, пересекающихся 34 линиями. Записываем два числа 34 + 55. Ниже самого верхнего цветка на стебле обычно располагаются цветы второго уровня, меньшие по размеру. Как правило, число пересекающихся линий у них равно 21 + 34. Еще ниже по стеблю могут располагаться цветы третьего уровня, выросшие последними. Число пересекающихся кривых у них равно 13 + 21.
В Оксфорде (Англия) для получения подсолнухов необычно большого размера растения удобряют, и количество пересекающихся дуг увеличилось с 34 + 55 до 55 + 89. Профессор Артур Чёрч (Arthur H. Church), новый ведущий специалист по этому очаровательному предмету, рассказал нам о гигантском экземпляре подсолнуха, выращенного в Оксфорде, у которого количество пересекающихся кривых равнялось 89 + 144.
В классификации растений наряду с множеством цветочных головок с зернами соседствуют цветы, у которых также просматриваются пересекающиеся линии в соцветии. Обычно их количество соответствует 5 + 8.
Если мы начнем считать фактическое количество листьев на стебле с самого низа растения вверх до цветочной головки, обходя вокруг стебля, то мы обнаружим, что минуем определенное количество листьев прежде, чем достигнем того, который расположен непосредственно над первым. Это количество листьев и количество обходов вокруг стебля являются величиной постоянной между каждой парой листьев, расположенных непосредственно друг над другом. Эти числа будут относиться к той же последовательности, что и числа продемонстрированные подсолнухами и цветами.
Числа, которые мы упомянули, принадлежат к арифметической прогрессии, так как каждый член последовательности представлен суммой предыдущих членов данного ряда, в нашем случае 2. Вот этот ряд чисел: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. Каждый член этой последовательности получен путем сложения двух предыдущих чисел.
Если мы возьмем любые два (соседних*) члена данной прогрессии и разделим один на другой, скажем 55 на 34, то мы получим некий коэффициент, и этот коэффициент является величиной постоянной для всей последовательности; то есть, любое число этого ряда, деленное на число, которое непосредственно предшествует ему, даст тот же коэффициент. Этот коэффициент 1.618 с бесконечной дробью. Если мы выполним обратную операцию и разделим 34 на 55, то получим число 0.618 с бесконечной дробью. Далее будет отмечено, что данные два результата различаются на единицу.
Кроме того, будет отмечено, что при выполнении этих двух операций деления присутствует незначительная погрешность. Это объясняется тем фактом, что данная последовательность не совсем точна для целых чисел. Следовало бы включить небольшую дробную часть. Несмотря на эту погрешность, в случае наблюдения за растениями целые числа сохраняются, чтобы облегчить сопоставление.
Является исключительным совпадением, что коэффициент 1.618 или 0.618 совершенно пленил древних греков. Исключительным, потому что они могли и не предполагать, что этот коэффициент связан с архитектурой растений. Они называли его особенной и превосходной пропорцией.
В средневековье он был назван Божественным сечением, а совсем недавно – Золотым сечением.”
Опытным путем я установил, что 144 является наибольшим числом, имеющим практическое значением. В законченном цикле фондового рынка количество волн Вторичного уровня (Minor) равно 144, как показано в таблице ниже и на рисунке 7 (Гл4):
Различные наблюдения
Западное полушарие состоит из 3 областей: Северная, Центральная и Южная Америка.
В западном полушарии находится 21 республика, каждая из которых является членом Всеамериканского Союза (Pan-American Union). В Северной Америке находится 3 страны: Канада, Мексика и Соединенные штаты. В Южной Америке находятся много республик и три Европейские колонии, всего 13. В Центральной Америке (прежний Панамский Канал) находится 5 республик.
Первоначально Соединенные Штаты состояли из 13 штатов. В настоящее время они делятся на 55 административных единиц: 48 штатов, округ Колумбия, Филиппины, Зона Панамского канала, Пуэрто-Рико, Аляска, Гавайские острова и Виргинские острова.
Под Декларацией Независимости стоят 56 подписей. Первоначальное количество – 55. Последняя была добавлена позже.
Главные ветви Федерального Правительства: 3.
Самый крупный салют в Армии: 21 орудие.
Избирательный возраст: 21 год.
Билль о правах содержит 13 пунктов.
Цвета национального флага: 3.
Страны Оси состояли из 3 партнеров. Германия поглотила 13 стран в стремительной последовательности, но забуксовала на четырнадцатой, России. Муссолини был диктатором 21 год.
в 1852 году Командующий эскадрой Перри (Perry) совершил в Японию визит вежливости и призвал “Сына Небес” нарушить абсолютную изоляцию. В 1907 году, 55 лет спустя, Япония всерьез угрожала Соединенным Штатам. В 1941 году, 34 года спустя (и через 89 лет после 1852 года), Япония атаковала Пирл-Харбор.
Памятник Вашингтону в г.Вашингтон, округ Колумбия (первый камень был заложен 4 июля 1848 года):
[Для наглядности приведу здесь фото из инета*]

Памятник Вашингтону.
Общая стоимость – $1 300 000 (13 Фибо).
Высота шпиля – 500 футов (5 Фибо).
Высота основания памятника – 55 футов (55 Фибо).
Площадь основание шпиля – 55 кв.футов (55 Фибо).
Верхушка шпиля – 34 фута (34 Фибо).
Ступени основания - 8 (8 Фибо).
Окна (по два на каждой стороне) - 8 (8 Фибо).
Глава V. Коррекции
Независимо от направления и размера, модели коррекций остаются идентичными. На бычьем участке рынка формируются нисходящие или боковые коррекции. На медвежьем участке – восходящие или боковые коррекции. Поэтому схематичные рисунки коррекций будут представлены и для бычьего, и для медвежьего участков рынка. Схематичные коррекции, показанные первыми, относятся к восходящим участкам рынка. Последующие диаграммы – к нисходящим участкам и будут “перевернуты”. Поэтому там, где встречается выражение “перевернуто”, оно имеет отношение к нисходящему основному тренду.
На рисунках 5, 6 и 7 обращалось внимание, что существует три уровня волн: Первичный (Major), Промежуточный (Intermediate) и Вторичный (Minor). Естественно, есть также и три уровня коррекций.
Существует три вида коррекций: зигзаг (1), волновая плоскость и треугольник.
Зигзаги
На рисунках 8, 9 и 10 представлены коррекции для восходящего тренда.
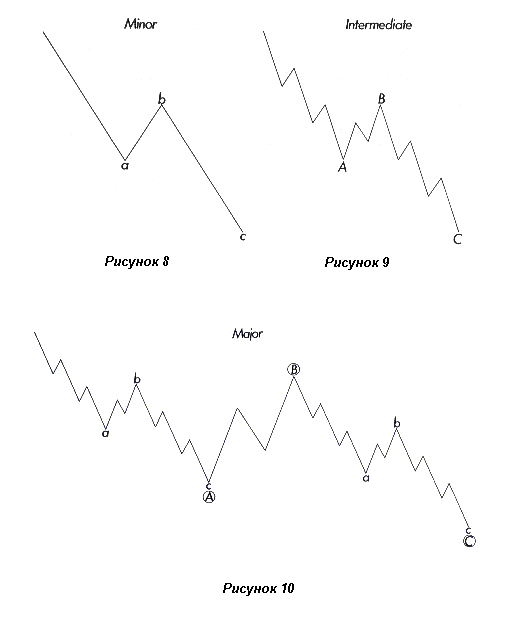
Рисунки 11, 12 и 13 перевернуты (коррекции для нисходящего тренда).
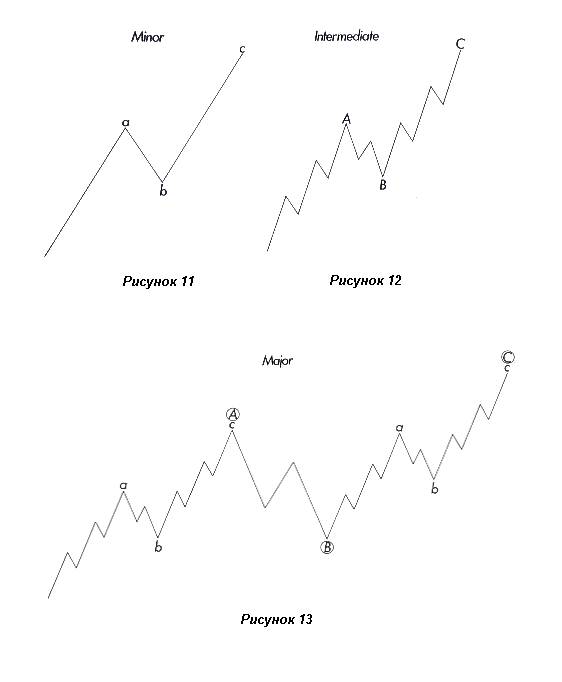
Волновые плоскости
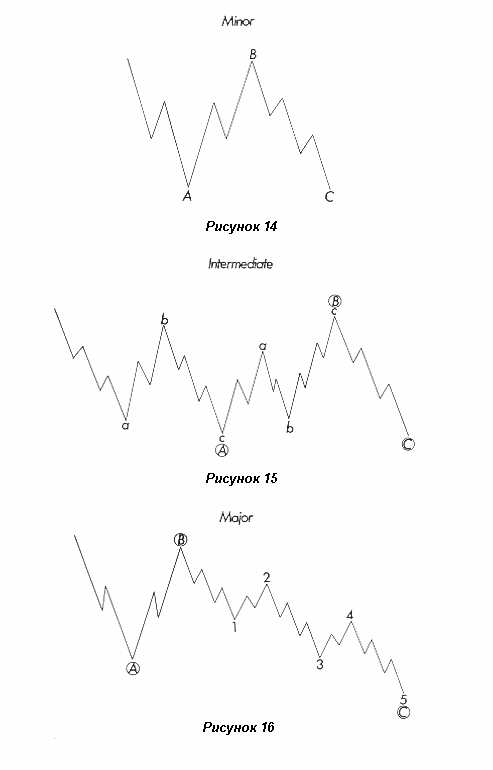
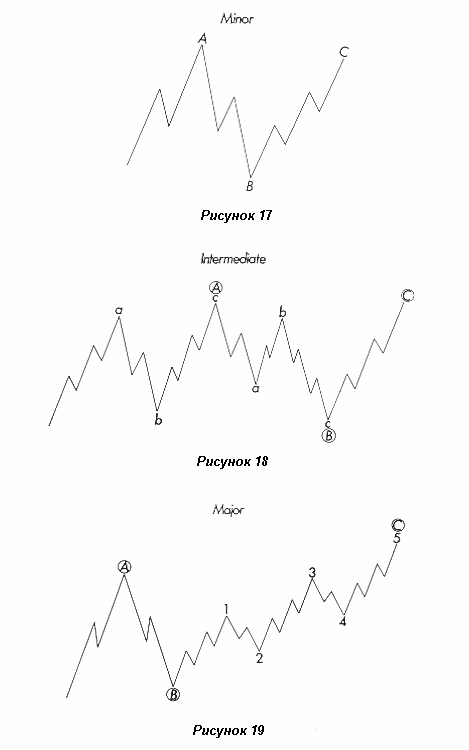
На последующих иллюстрациях представлены волновые плоскости Вторичного (Minor), Промежуточного (Intermediate) и Первичного (Major) уровней (рисунки 14, 15 и 16) и перевернутые варианты (рисунки 17, 18 и 19). Этим схематичным изображениям дано название “плоскость” по той причине, что их обычная внешняя форма – горизонтальная. Временами они имеют нисходящий или восходящий наклон.
Собственно говоря, эти модели можно было назвать “3-3-5”. По результатам последних исследований, они являются трех-волновыми моделями, т.е., А, В и С, в то время как бычья модель (импульс*) является моделью "5-3-5-3-5" для волн 1, 2, 3, 4 и 5.
Модель человека - "5-3-5-3". От торса отходят 5 выступающих частей (голова, две руки и две ноги); руки и ноги подразделяются на 3 части; концы рук и ног разделяются на 5 пальцев; каждый палец (кроме большого пальца ног) опять-таки разделяется на 3 части.
Будет ли волна С волновой плоскости удлинением или нет, но модель останется коррекционной. Тем не менее, сформируется ли удлинение в волне С можно узнать, внимательно прочитав Главу 8 “Чередование”.
Сложные коррекции
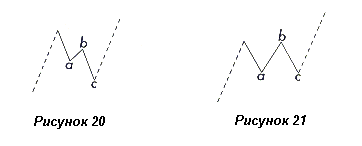
Коррекция на Вторичном волновом уровне (Minor) может состоять из трех волн, как показано на рисунках 20 и 21.
Двойная коррекция, формирующаяся вбок, может состоять из семи волн, как показано на рисунке 22. У тройной коррекции, развивающейся вбок, может быть одиннадцать волн, как показано на рисунке 23.
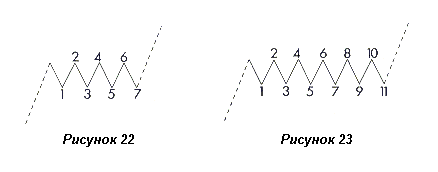
Другими словами, боковая коррекция восходящего тренда всегда заканчивается нисходящей волной (2), состоит ли она из одной, трех, семи или одиннадцати волн. Их называют так: три волны – это “одинарная тройка”, семь волн – это “двойная тройка”, а одиннадцать волн – “тройная тройка”.
Такое же количество восходящих волн, как показано на рисунках 24, 25 и 26, является коррекционным.
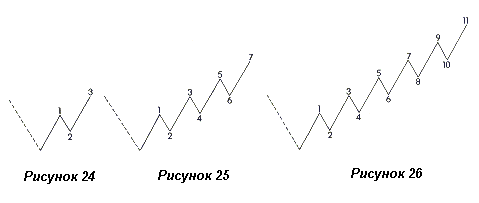
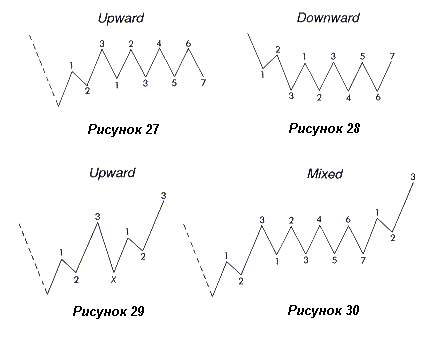
Иногда эти тройки разнородны по направлению: восходящая и боковая или нисходящая и боковая, как показано на рисунках 27 и 28 (смешанные двойные тройки; (3)), а также на рисунках 29 и 30 (восходящие двойные тройки).
Треугольники
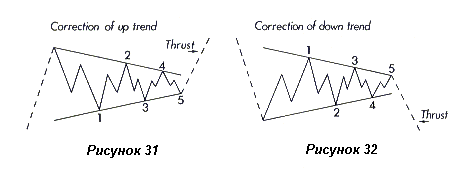
Треугольники состоят из пяти волн или лучше сказать из пяти отрезков (legs). В крупных образцах, каждый отрезок будет состоять из трех волн, как показано на рисунках 31 и 32.
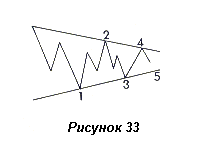
В образцах среднего размера четвертый и пятый отрезки могут состоять из одной волны каждый, как показано на рисунке 33. На мелких образцах отрезки часто состоят всего из одной волны. Основным ориентиром в формировании треугольника являются образующие, т.е., прямые линии, проведенные через его вершины. Нельзя быть уверенным в том, что формируется треугольник до тех пор, пока не начнется пятая волна.
На рисунке 34 показаны три существующих типа треугольников (4).
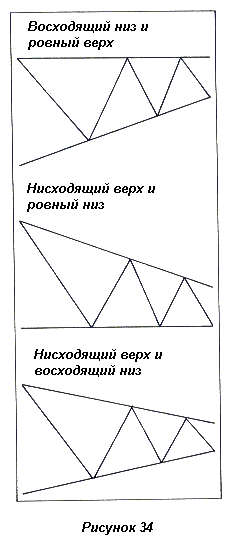
Пятый отрезок может завершиться в пределах или вне пределов образующих треугольника (5), как показано на рисунках 35 и 36.

Пятая волна может состоять из трех волн, если только треугольник не слишком мал. В одном случае треугольник формировался всего семь часов. Самый большой треугольник, сформированный между ноябрем 1928 и апрелем 1942 года, длился тринадцать лет (6). Эта формация будет обсуждаться в других главах.
Движение, следующее за пятым отрезком треугольника, называется “выпад” ("thrust"; бросок цены*). Оно будет состоять из пяти волн и совпадать по направлению с отрезками 2 и 4 треугольника.
Треугольники встречаются нечасто. Когда они формируются, то занимают положение четвертой волны (импульсного*) восходящего или нисходящего движения любого волнового уровня, как показано на рисунках 37 и 38.
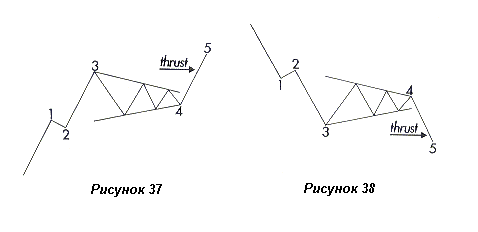
Пятая волна (данного импульса*), которая следует за треугольником, называется “бросок” ("thrust") и состоит из пяти волн подобно волнам 1 и 3. Как показано выше, пятая волна заходит за вершину волны 3 (рисунки 37 и 38).
++++++++++++++++++++
СНОСКИ
(1) В действительности, на рисунках 10 и 13 представлены “двойные зигзаги”, которые Эллиотт рассматривает в главе 6. Или Эллиотт перепутал здесь иллюстрации, или он полагал, что двойные зигзаги более распространены на Первичном уровне, чем обычные зигзаги. Для иллюстрации истинного зигзага Первичного уровня, обратитесь к части [A]-[B]-[C] рисунка 7, а также к рисунку 27 Закона волн.
(2) При подготовке рисунков 27 и 28 Эллиотт упустил это утверждение. Неумышленно он пропустил дополнительную “тройку” в каждой коррекции, и, следовательно, последующее движение не может быть возобновлением тренда, который был до коррекции.
(3) То же.
(4) Эти иллюстрации представляют восходящий, нисходящий и симметричный (сходящиеся) треугольники. По неустановленной причине Эллиотт не включил описание перевернутого симметричного (расходящегося) вида.
(5) Пятая волна треугольника может завершиться вне образующих треугольника, но не за пределом вершины третьей волны треугольника.
(6) См. сноски 1-8 к Главе XI.
(7) Кроме того, их можно найти на месте волны В.
Глава VI. Удлинения
Удлинение может сформироваться в любом одном из трех импульсов, т.е., волнах 1, 3 или 5, но никогда в более, чем одном, как показано на рисунках 39, 40 и 41 (для восходящего движения) и на рисунках 42, 43 и 44 (перевернуто).
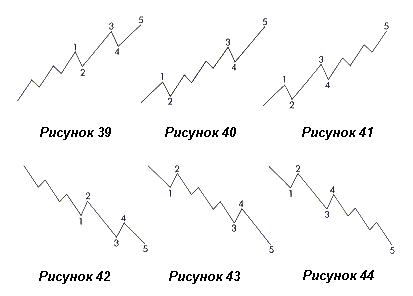
Следует обратить внимание, что в каждом примере общее количество волн равно девяти, если удлинение считать в качестве пяти волн вместо одной. В редких случаях удлиненное движение может состоять из девяти волн равного размера, как показано на рисунках 45 и 46.
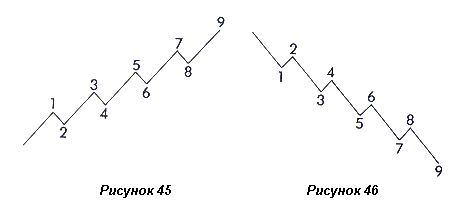
Удлинения формируются только на новой ценовой территории текущего цикла. То есть, они не формируются в качестве коррекций
Удлинение в удлинении
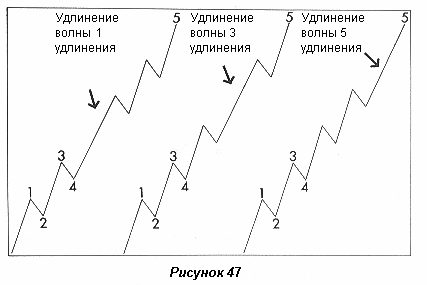
Ошибочная разметка
Три импульсные волны 1, 3 и 5 редко бывают одной длины. Одна из этих трех волн бывает значительно длиннее, чем любая из двух других. Важно отметить, что волна 3 никогда не бывает короче обеих (3) волн 1 и 5. Например, если волна 3 короче, чем или волна 1, или 5, как показано на рисунке 49, правильный способ разметки представлен на рисунке 50.

Обратите внимание, что волна 4 заходит на территорию волны 1, что ей не следует делать. Такой перехлест означает, что окончание волны 4 находится ниже, чем вершина волны 1. Перевернутый пример будет выглядеть как показано на рисунках 51 и 52.

Перехлест в “сложной” волновой структуре требует тщательного изучения. Подчас сложные структуры формируют “двойные тройки” или “тройные тройки”, как проиллюстрировано в главе 5.
Боковые движения
Как было отмечено, все коррекционные движения не зависимо от волнового уровня состоят из трех волн. Боковые движения следуют такой же манере поведения и также являются коррекционными. Рисунок 58 представляет два вида боковых движений (6), следующих за восходящим трендом. На рисунке 59 основной тренд – нисходящий.

++++++++++++++++++++
СНОСКИ
(1) Несомненно, часть удлинения в первой или третье волне будет пройдено дважды, но это будет выполнено не в такой манере, как в случае с пятой волной. Только после удлинения в пятой волне откат доходит до вершины второй волны удлинения.
(2) Волновой уровень не оказывает влияние на модели. Данное утверждение относится к вершине растянутой волновой плоскости, за которой предположительно последовал двойной проход, и является результатом необычной разметки Эллиоттом периода 1928-1930 г.г.
(3) Он имеет в виду “короче, чем волна 1, и короче, чем волна 5”.
(4) То же самое.
(5) Эти модели едва ли являются волновой плоскостью по внешней форме. Общий контур предполагает двойной зигзаг. Вероятно, этот материал является результатом склонности Эллиотта размечать удлиненные пятые волны там, где фактически удлиняется третья волна, тем самым оставляя пару “дополнительных” волн в конце (движения*), которые он маркирует в качестве А и В.
(6) Первый пример на рисунках 58 и 59 является волновой плоскостью. Второй просто показывает облик некой волновой плоскости, но тайм-фрейм достаточно большой, чтобы увидеть ее детали.
Глава VIII. Чередование
Согласно словарю, чередование – есть “появление или воздействие двух объектов или серии объектов по очереди”. Чередование – это закон природы. Например, листья или ветки появляются сначала на одной стороне стебля, а затем на противоположной стороне, меняя свое положение. Строение человеческого тела следует следующему правилу: 5-3-5-3-5. Можно было бы привести бесконечный список примеров, но тема данной главы – характер поведения чередования в области человеческой деятельности.
Чередуются бычьи и медвежьи рынки. Бычий рынок состоит из пяти волн, а медвежий – из трех. Таким образом, чередуются пять и три. Одно и то же правило действует на всех волновых уровнях.
Бычье движение состоит из пяти волн. Волны 1, 3 и 5 являются восходящими. Волны 2 и 4 – нисходящими или боковыми. Таким образом, нечетные числа чередуются с четными.
Волны 2 и 4 являются коррекционными. В этих двух волнах чередуются модели. Если волна 2 является “простой”, то волна 4 может быть “сложной” и наоборот. “Простая” коррекция на младших волновых уровнях состоит из одной нисходящей волны. “Сложная” - состоит из трех нисходящих или боковых волн. См. рисунки 62 и 63.

На старших волновых уровнях, на длительных бычьих и медвежьих рынках коррекционные волны соответственно крупнее и подготовка к завершающему падению зачастую является весьма утомительной. Сначала проявляется более-менее значительное нисходящее движение, которое я маркирую заглавной А. За ним следует восходящая волна, обозначенная в качестве волны В. Третье и последнее движение вниз является волной С. Волна А может быть зигзагом. В этом случае волна В может быть перевернутой волновой плоскостью. Если волна А является волновой плоскостью, то волна В может быть перевернутым зигзагом. (В любом случае волна С будет состоять из пяти нисходящих волн. Она может быть мощной и может достичь начальной точки предыдущего бычьего рынка.) Таким образом, волны А и В чередуются.
Тринадцатилетний треугольник демонстрирует еще один пример чередования. С ноября 1928 года по 31 марта 1938 года сформирована волновая плоскость. (1) С 31 марта 1938 года по октябрь 1939 года – перевернутый зигзаг. С октября 1939 года по май 1942 – сформирована волновая плоскость. (2)
[См. рисунок 71 из главы X. Волны [1]-[2]-[3] в данном варианте автор считает волновой плоскостью. Оба варианта подробно разбираются в главе XI.*]
Вершина растянутой волновой плоскости – это один из случаев, когда волна В превышает вершину пятой волны предыдущего бычьего рынка, как пояснялось в Главе 7. Даже здесь присутствует чередование. Вершина 1916 года была вершиной растянутой волновой плоскости, 1919 года – обычная, 1929 года – вершина растянутой волновой плоскости, 1937 года – обычная.
Вплоть до 1906 года железнодорожный индекс Доу опережал в восходящих движениях [промышленный индекс DJIA*]. В течение 34 лет (Фибо) с 1906 по 1940 год в восходящих движениях лидировал промышленный индекс Доу. С 1940 года вновь лидирует железнодорожный индекс.
++++++++++++++++++++
СНОСКИ
(1) См. сноски (4) и (5) к главе XI Закона природы.
(2) В действительности этот участок или “пятерка”, или содержит часть треугольника в составе волны В, а затем следует пяти-волновая С. Или разметка завершает А-В-С с 1937 года. См. Сноску 8 к Главе XI Закона волн.
Глава IX. Шкалы
Применение исключительно или полулогарифмической, или арифметической шкалы в качестве широко распространенной привычки является ошибочной практикой и лишает исследователя выгодности и достоинства этих шкал. Всегда следует применять арифметическую шкалу до тех пор, пока не потребуется логарифмическая.Во время восходящего пяти-волнового движения “базовая линия” строится по вершинам волн 2 и 4, а затем через вершину волны 3 проводится “параллельная линия”. Пример представлен на рисунке 64.

Как правило, волна 5 может завершиться приблизительно у параллельной линии, если применяется арифметическая шкала. Тем не менее, если волна 5 значительно превысила параллельную линию, а структура волны 5 показывает, что она еще не завершила свою модель, тогда все движение от начала волны 1 следует представить с помощью полулогарифмической шкалы. Окончание волны 5 (в этом случае*) может достичь, но не превысить параллельную линию. Например, если одну и ту же волновую конструкцию представить с помощью обеих шкал, то график может выглядеть как показано на рисунках 65 и 66.
Когда наблюдается прорыв (inflation (1)), возникает необходимость в полулогарифмической шкале. Если применяется полулогарифмическая шкала, а прорыва нет, то волна 5 может значительно не дойти до параллельной линии, как показано на рисунке 67.


++++++++++++++++++++
СНОСКИ
(1) “Инфляция” (“Inflation”), как позже Эллиотт даст определение в главе 12, является не денежной инфляцией, как мы привыкли (см. сноску 1 к главе XII). [Я позволил перевести данный термин, как “прорыв”, что наиболее точно передает его смысл в данном контексте.*]
Определяющим фактором в применении арифметической или логарифмической шкалы является просто форма волны. Если арифметическая шкала правильно отражает форму, то движение измеряется в пройденных пунктах. Если форма правильно отражается в логарифмической шкале, то пройденное движение отслеживается в относительных процентах. Каждый может взять один и тот же участок графика, и разметить на нем идеальные волны Эллиотта как с использованием арифметической шкалы, так и с использованием логарифмической.
Глава X. Примеры
Наглядный показ Закона волн на предыдущих страницах был сделан для того, чтобы облегчить понимание следующих графиков. (1)

На рисунке 68 представлен индекс Axe-Houghton-Burgess с 1857 по 1932 год на полулогарифмической шкале. Это самый крупный волновой уровень, для которого есть данные. Обратите внимание на пять волн с 1857 года по ноябрь 1928 года. Кроме того, обратите внимание, что базовая линия проведена по вершинам волн 2 и 4, а параллельная линия – через вершину волны 3. Окончание волны 5 касается параллельной линии в ноябре 1928 года.
Все движение целиком представляло собой прорыв вверх; следовательно, была необходима полулогарифмическая шкала. Тем не менее, при нанесении на отдельные графики нескольких бычьих рынков вполне подходила арифметическая шкала.
Заметьте, что падение до 1932 года как раз достигло начала волны 5 1896 года. Именно на низшей отметке 1896 года прекратилось падение 1929-1932 годов – другими словами, стандартная коррекция. Незнание прошлой истории является причиной ошибочного использования термина “Великая депрессия”, и, следовательно, подчеркивает в этом жизненную важность истории, как и всех других проявлений человеческой деятельности.
На рисунке 69 представлена детальная структура волны 5 с рисунка 68 и использованием полулогарифмической шкалы. Она разделяется на пять волн следующего меньшего уровня.

На рисунке 70 представлен график индекса DJIA за период с 1921 по 1928 годы с использованием полулогарифмической шкалы. Обратите внимание, что базовая линия проведена по вершинам волн 2 и 4, а параллельная линия – через вершину волны 3. Волна 5 как раз касается этой линии.

Движение с 1857 года по ноябрь 1928 состоит из пяти волн, как показано на рисунке 68. Пятая волна с 1896 года подразделяется на пять волн, как показано на рисунке 69. Пятая волна этого движения, начинаясь в 1921 году, опять разделяется на пять волн, как показано на рисунке 70. Другими словами, все движение с 1857 года подразделяется на три уровня.
На рисунке 71 представлен график индекса DJIA с использованием арифметической шкалы и снова (2) длина волн 1 и 3 составляет 62% от волны 5.
С 1857 по 1928 год сформировалось семь бычьих рынков и шесть медвежьих, всего – 13 (Фибо). (3) Все бычьи рынки с 1857 по 1928 год были обычными по протяженности. Не забудьте, что с 1921 по 1928 год было три бычьих рынка и два медвежьих, а не один бычий. Эти два медвежьих рынка были необычными по протяженности.
Фактор времени весьма важен, потому что он, как правило, подтверждает модель и соответствует модели. Например, с 1928 по 1942 – 13 лет (Фибо). С 1937 по 1942 – 5 лет (Фибо). Оба периода завершаются одновременно. Все движение с 1928 по 1942 год представляет собой одну модель – треугольник. Каждая волна треугольника равна 62% от предыдущей. Все три фактора – модель, время и соотношение волн – идеальны и соответствуют ряду и коэффициентам Фибоначчи. См. рисунок 71.
В предыдущем материале был изложен Закон природы. Числа из ряда Фибо применяются тремя способами: количество волн, время (количество дней, недель, месяцев или лет) и соотношение чисел из ряда Фибо, 62%.

++++++++++++++++++++
СНОСКИ
(1) Чтобы представить обзорную картину на главном волновом уровне (Grand Supercycle), см. рисунок 1 заметки “Будущая модель рынка”, так же как и рисунок 98 в конце этой книги. [Для наглядности приведу их ниже.*]

(2) “Снова” подразумевает восходящий рынок, представленный на рисунке 69, и подъем в 1932-1937 годах, представленный на рисунке 72. Просто поразительное повторение.
(3) Вероятно, Эллиотт принимает первую восходящую волну в качестве одного бычьего рынка, а третью и пятую восходящие волны – в качестве трех бычьих рынков каждую.
Глава XII. Прорыв
Термин “прорыв” ("inflation") определяется в словаре как “распространение за пределы естественных границ”. Отдельно взятый участок бычьего рынка не нарушит “естественных границ”. Последовательность таких участков один над другим, может выйти “за естественные границы“. Отдельный бычий участок рынка, как правило, не бывает “над другим” если только они не чередуются с необычными медвежьими рынками (неглубокие откаты*).
В двадцатые годы из-за необычных медвежьих рынков был сформирован прорыв (1). Во время этого периода было три обычных бычьих рынка и два необычных медвежьих, всего пять. Предупреждения о прорыве происходило в следующем порядке: обычная волна 1, необычная волна 2, обычная волна 3, необычная волна 4 и прокол волной 5 параллельной линии на арифметической шкале (см. рисунок 65, Глава 9).
Рисунок 75 демонстрирует обычный бычий рынок и обычную медвежью коррекцию (волны a, b и c), которая глубоко откатилась вниз после пробития базовой линии. На рисунке 76 представлена необычная медвежья коррекция, которая едва пробила базовую линию.

На рисунке 77 представлен график индекса Доу (DJIA) с 1921 года по ноябрь 1928 года на арифметической шкале. Волна 5 пробивает параллельную линию. Факт пробития параллельной линии требует перевода всего графика с 1921 года на логарифмическую шкалу. Рисунок 78 демонстрирует тот же индекс (месячный тайм-фрейм) на логарифмической шкале. Волна 5 касается, но не пробивает параллельную линию.

Существует три способа заблаговременного определения, в какой точке завершится прорыв: тот, который описан выше (с помощью логарифмической шкалы*), соотношение волн (показан на рисунке 71) и временной фактор (показан на рисунке 71).
++++++++++++++++++++
СНОСКИ
(1) Эллиотт использует буквальное определение инфляции, а не кредитно-денежное (к которому мы привыкли*). По его определению “прорыв” (“inflation”) формируется на рынках, которые испытывают ускорение по отношению взлета цены к единице времени. Смотрите сноску (1) к главе IX.
[Я позволил перевести данный термин, как “прорыв”, что наиболее точно передает его смысл в данном контексте.*]
Глава XIII. Цена золота
Цена на золото – еще один пример, как в
