Построение геометрических образов в системе autocad.

Для построения геометрических образов в системе AutoCADрассмотрим следующие поверхности вращения:

1) Сфера;

2) Цилиндр;

3) Конус.

Рис. 1. Общий вид геометрических образов: сфера, цилиндр, конус.

Рис. 2. Фронтальная проекция поверхностей вращения: сфера, цилиндр, конус.

Для создания геометрических образов будут использоваться такие примитивы построения как отрезок, полилиния, прямоугольник, круг, дуга, эллипс.

ПОСТРОЕНИЕ ЦИЛИНДРА.

Для обеспечения точности построений в системе AutoCADприменяются режимы объектной привязки, позволяющие производить построения рисунка по отношению к различным характерным точкам. Рекомендуется включить данный набор привязок.(Рисунок 3). Для этого необходимо щелкнуть правой кнопкой мыши на кнопке объектной привязки и поочередно щелкнуть левой кнопкой мыши на нужные привязки.

Рис 3. Панель объектной привязки

Построение цилиндра начнем с прямоугольника , для того чтобы задать размеры необходимо в графическом поле после выбора команды «Прямоугольник» щелкнуть сначала левой кнопкой мыши для выбора положения будущей фигуры, а затем правой кнопкой мыши и выбрать из выпадающего меню вкладку «Размеры».

а) б) в)

Рис. 4. Построение прямоугольника по размерам. а) Выбор команды; б) Щелчок левой кнопкой мыши; в) Меню выбора параметров.

Зададим длину прямоугольника введем с клавиатуры 600 нажимаем «Enter»,далее введем ширину 800 нажимаем «Enter». Щелкаем левой кнопкой мыши, фигура создана.

Рис. 5. Прямоугольник с размерами 600х800 ед.

С помощью инструмента «Полилиния» ,построим секущую призму (произвольно).

Выбираем инструмент «Полилиния» и создаем два произвольных отрезка, в конце построения нажимаем «Enter».

Рис. 6. Произвольное сечение прямоугольника.

(фронтальная проекция)

Обрезаем лишние линии прямоугольника командой «Обрезать» .

а) б)

Рис. 7. а) До обрезки; б) После обрезки (фронтальная проекция)

Чертим две проекции в виде примитивов с помощью инструментов «Прямоугольник» и«Круг» . Диаметр круга 600 ед. соответственно.

Нанесем обозначения точек проекций с помощью команды «Текст» .

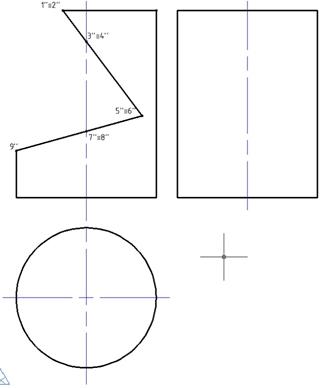
Рис. 8. Изображение цилиндра в трех плоскостях проекций П₁, П₂, П₃.

Строим линии проекций с помощью инструмента «Отрезок» и во вкладке свойств объекта меняем тип линии на штрихпунктирную «ACAD_ISO08W100»,масштабу типа линии присваиваем значение «25», а для визуального удобства меняем цвет линий на «Синий».Для этого выбираем нужные отрезки левой кнопкой мыши, щелкаем правой и в выпадающем меню выбираем вкладку «Свойства».

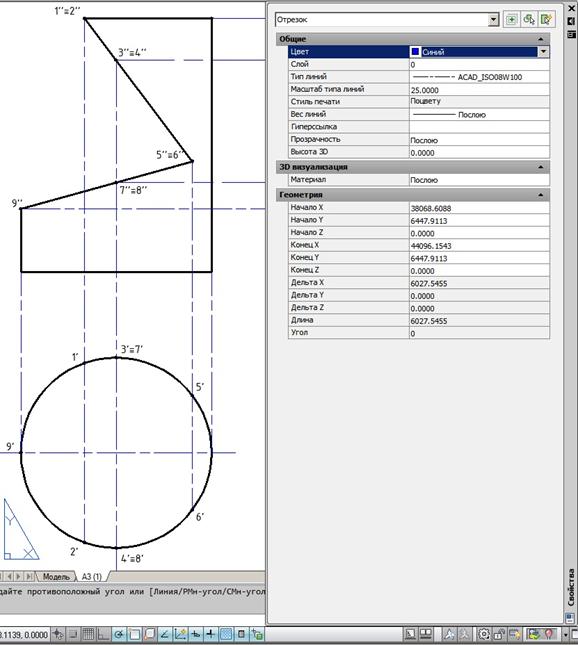
Рис. 9.Настройка свойств линий проекции (отрезков).

Достраиваем видимые и невидимые линии «Отрезком»,назначаем необходимые типы линий сплошная и штриховая соответственно. Горизонтальная проекция готова.

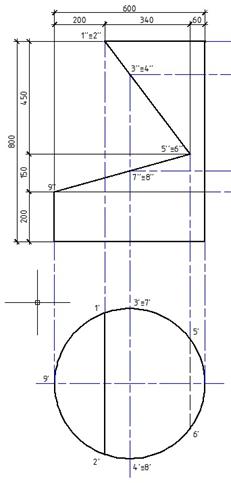
Рис. 10.Горизонтальная проекция.

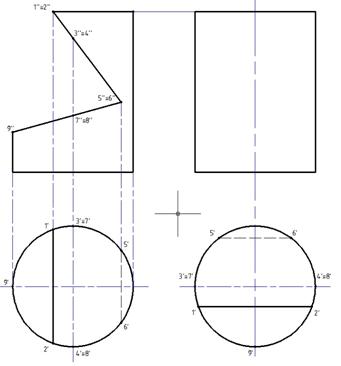Для удобства графического построения профильной проекции, рекомендуется скопировать горизонтальную проекцию под будущей профильной проекцией, обязательно сопоставить оси проекций, затем повернуть на 90º против часовой стрелки относительно её центра.

Рис. 11.Подготовка

к построению профильной проекции.

Построим точки проекций 1''', 2''', 5''' и 6''' на пересечении проекций 1' и 1'', 2' и 2'', 5' и 5'', 6' и 6'' соответственно.

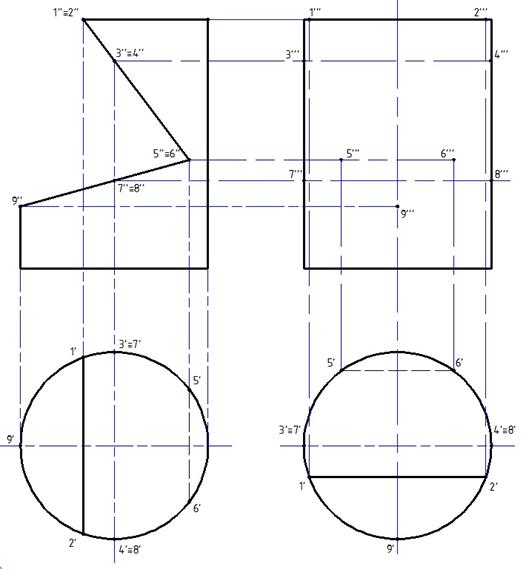
Рис. 12. Построение проекций точек на профильной проекции.

Для дальнейшего построения линий сечения 1-3-5(''') и 2-4-6(''') необходимо создать вспомогательную линию на фронтальной проекции.

С помощью привязок «Продолжение» и «Пересечение» достроим вспомогательную линию от точки 5''=6'' до грани цилиндра.

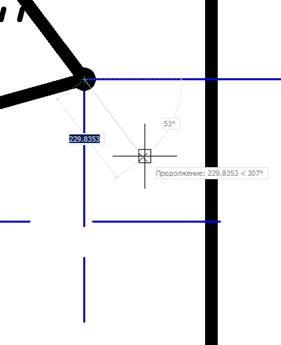
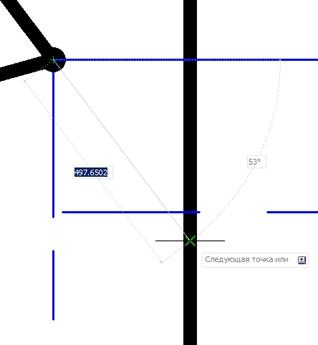
Рис. 13. Построение вспомогательной линии.

Повторим от точки 1''=2''. Проводим линии проекций и получаем вершины сечения.

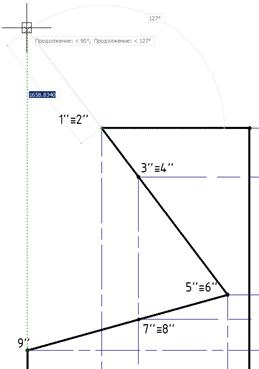
Рис. 14. Построение вспомогательной линии

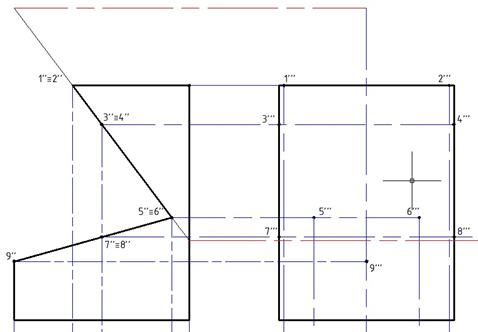
Рис. 15. Линии проекции вершин сечения

Создадим сечение инструментом «Эллипс» , правой кнопкой мыши выберем параметр «Центр», и укажем будущий центр эллипса.

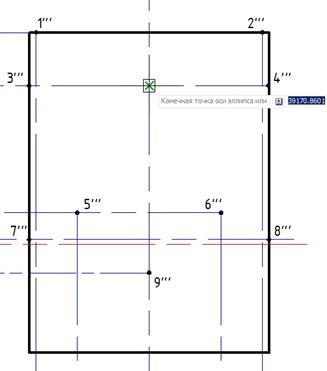
Рис. 16. Выбор центра эллипса.

Укажем конечную точку оси эллипса в точке пересечения вспомогательной линии с осью проекции и длину другой оси в точке 3''' или 4'''.

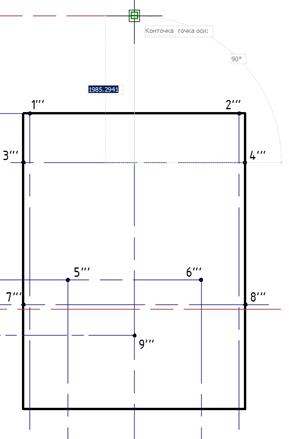
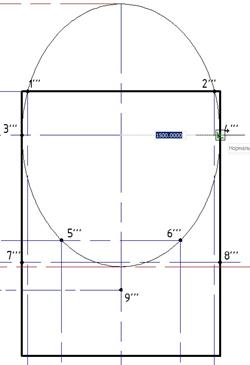
а) б)

Рис. 17. а) Вершина первой оси эллипса; б) Вершина второй оси эллипса.

Полученную фигуру обрежем по проекционным линиям 1'''-2''' и 5'''-6''' с помощью инструмента «Обрезать».

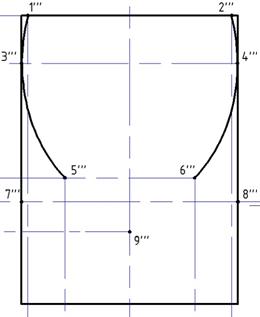
Рис. 18. Обрезка лишних линий эллипса.

Таким же образом чертим эллиптическое сечение с центром в точке пересечения оси проекции и линии проекции точек 7" и 8".

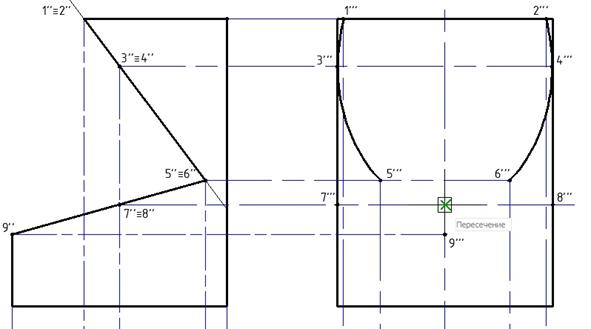
Рис. 19. Выбор центра второго эллипса.

Одна вершина оси точка 9''', другая вершина оси точка 7''' или 8'''. Лишние линии обрезаем. Чертим видимую линию сечения 5'''-6'''.

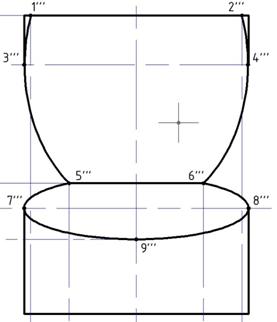
Рис. 20. Фронтальная проекция.

Оформляем работу.

Методические указания по выполнению графических работ

При изучении начертательной геометрии предусматриваются: лекционные и практические занятия, самостоятельная работа с учебником и учебными пособиями, решение типовых задач каждой темы курса, выполнение графической работы, консультации по курсу, зачет.

Перед изучением курса необходимо ознакомиться с программой, приобрести учебную литературу, чертежные инструменты и принадлежности (линейки, угольники, транспортир, карандаши, циркуль, резинку, чертежную доску формата А3, ватман формата А3).

Начертательную геометрию нужно изучать строго последовательно и систематически. Перерывы в занятиях, как и перегрузки нежелательны. Для этого нужно тщательно продумать календарный рабочий план самостоятельной учебной работы, согласуя его с учебным графиком и планом по другим учебным дисциплинам первого семестра.

В начертательной геометрии следует избегать механического запоминания теорем, отдельных формулировок и решений задач. Такое запоминание непрочно. Необходимо усвоить прочитанный в учебной литературе материал. При изучении того или иного материала курса студенту необходимо проверить свои знания ответами на поставленные в конце каждой темы учебника вопросы. Студент должен разобраться в теоретическом материале и уметь применить его в решении конкретных задач.

Каждую тему курса желательно прочитать по учебнику дважды. При первом чтении необходимо глубоко и последовательно изучить весь материал темы. При повторном изучении темы рекомендуется вести конспект, записывать в нем основные положения теории, теоремы курса и алгоритма решения типовых задач. Конспектирование лекций можно заменить учебным пособием [12]. При подготовке к экзамену учебное пособие не может заменить учебника.

Особое внимание должно быть уделено решению задач, т.к. это наилучшее средство для изучения основных положений теории. Перед решением задач необходимо понять ее условие и четко представить алгоритм решения, т.е. установить последовательность выполнения операций.

Если в процессе изучения курса начертательной геометрии у студента возникли трудности, то ему необходимо обратиться за консультацией к преподавателю кафедры.

Задания для графической работы индивидуальны и берутся в соответствии с вариантами из таблиц. Студент выполняет тот вариант задания, номер которого соответствует сумме двух последовательных цифр шифра его зачетной книжке. Если, например, номер шифра в зачетной книжке (студенческого билета) - № 0612000519, то студент во всех заданиях контрольной работы выполняет 10 (десятый) вариант.

Задачи контрольной работы выполняются на листах чертежной бумаги формата А3 (297 х 420 мм). Слева, вдоль короткой стороны листа, на расстоянии 20 мм проводится рамка поля чертежа. С трех других сторон листа проводится рамка поля чертежа на расстоянии 5 мм. В правом нижнем углу формата вплотную к рамке помещается основная надпись (рис.1).

Все надписи, как и отдельные обозначения, в виде букв и цифр в графической работе (ГР), должны быть выполнены стандартным шрифтом размером 5 и 7 в соответствии с ГОСТ 2.304-81 (рис. 2, 3).

Рис. 1

Построение задач выполняется с помощью чертежных инструментов. На качество построений должно быть обращено особое внимание. Небрежное построение может привести к неправильным результатам.

При обводке построений характер и толщина линий берутся в соответствии с ГОСТ 2.303-68. Линии видимого контура обводятся сплошными толстыми основными линиями мягким карандашом (ТМ, М) толщиной s = 0,8…1,0 мм. Линии центров и осевые – штрихпунктирной линией толщиной от s/2 до s/3 мм твердым карандашом (Т). Линии построений и линии связи должны быть сплошными и наиболее тонкими s = 0,3 мм. Линии невидимого контура выполняются тонкими штриховыми линиями толщиной от s/2 до s/3 мм.

Желательно при обводке ответа использовать красную пасту. Точки на чертежах желательно вычерчивать в виде окружности 1,5…2 мм с помощью специальной линейки.

Каждая графическая работа сопровождается алгоритмом решения задачи, который записывается на отдельном листе писчей бумаги или бумаги в клетку.

Первый лист (титульный) контрольной работы оформляется по образцу (приложение 1).

Выполнив все задачи графической работы, студент передает ее на рецензию. После проверки работы и опроса-собеседования по ней, получив у преподавателя отметку «Зачтено», студент имеет право быть допущенным к дальнейшему виду испытания к экзамену или зачету.

Преподаватель вправе аннулировать представленное задание, сообщив об этом на кафедру, если при собеседовании убедится, что студент выполнил графическую работу не самостоятельно.

Рис. 2

Латинский алфавит

1 – альфа 2 – бета 3 – гамма 4 – дельта

5 – эпсилон 6 – дзета 7 – эта 8 – тэта

9 – йота 10 – каппа 11 – ламбда 12 – мю

13 – ню 14 – кси 15 – омикрон 16 – пи

17 – ро 18 – сигма 19 – тау 20 – ипсилон

21 – фи 22 – хи 23 – пси 24 – омега

Рис. 3

Символы и обозначения

1.2.1 Обозначения:

1. Точки – обозначаются прописными буквами латинского алфавита: А, В, С, D,

E, F, G, H, M, N, O, R, … или арабскими цифрами 1, 2, 3, 4, … .

2. Линии (прямые и кривые) – строчными буквами латинского алфавита: a, b, c, d,

e, f, g, h, m, n, o, r, … .

Прямые линии также обозначаются:

(АВ) – прямая, проходящая через точки А и В;

[АВ) – луч, ограниченный точкой А и проходящий через точку В;

[АВ] – отрезок прямой, ограниченный точками А и В;

│АВ│– натуральная величина отрезка [АВ] (равная оригиналу);

O(О, R) – окружность с центром в точке О, радиуса R.

3. Оси проекций -х, у, z, где х – ось абсцисс; у – ось ординат; z – ось аппликат.

4. Поверхности и плоскости – прописными буквами греческого алфавита:

Г(гамма), Ф(фи), S(сигма), W(омега), Q(тета), Y(пси), L(лямбда), D(дельта), P(пи), R(ро), … .

Плоскости – основной (координатной) системы плоскостей проекции обозначают прописными буквами П, греческого алфавита с добавлением надстрочного или подстрочного индекса:

П₁ – горизонтальная плоскость проекций (координатная плоскость Оху);

П₂ – фронтальная плоскость проекций (координатная плоскость Охz);

П₃ – профильная плоскость проекций(координатная плоскость Оzу).

Дополнительные плоскости проекций в дополнительной системе плоскостей проекций обозначают П₄, П₅, … .

5. Углы обозначают строчными буквами греческого алфавита: a, b, d(дельта), j(фи), g, w(омега), … . Ða^o, Ðb^o, … ;

Ð АВС – угол с вершиной в точке В. _^

^ - угловая величина (градусная мера); АВС – величина угла АВС.

6. Проекции точек, прямых и кривых линий обозначают теми же буквами, как и оригиналы с добавлением индекса, соответствующего индексу плоскости проекций. На плоскости П₁ – А₁, а₁;на плоскости П₂–А₂, а₂; и т.д.

Последовательность геометрических фигур обозначают теми же буквами с добавлением надстрочного индекса: точек - А¢, А², А²¢, …; линий - а¢, а², а²¢, …; поверхностей - S¢, S², … .

7. Особые прямые и плоскости имеют постоянные обозначения:

7.1. Линии уровня:

h – горизонтальная прямая уровня (горизонталь);

f – фронтальная прямая уровня (фронталь);

p – профильная прямая уровня.

7.2. Проецирующие плоскости:

Г – горизонтально-проецирующая плоскость;

Ф – фронтально-проецирующая плоскость;

Р – профильно-проецирующая плоскость.

7.3. Следы проецирующих плоскостей:

Г₁– горизонтальный след плоскости Г на П₁;

Ф₂ – фронтальный след плоскости Ф на П₂.

7.4. Оси вращения – i, j.

8. Способы задания геометрического образа указываются в скобках рядом с его буквенным обозначением:

(А, В) – прямая задана двумя ее точками А и В;

Σ (А, В, С) – плоскость Σ задана тремя ее точками А, В, С;

Ρ(а ∩ b) – плоскость Ρ задана пересекающимися прямыми а и b;

Σ (ℓ, А) – плоскость Σ задана прямой ℓ и точкой А;

Σ(а ççb) – плоскость Σ задана параллельными прямыми а и b;

Φ(ℓ, i) – поверхность Φ определяется образующей ℓ и осью вращения i.

9. Центр проецирования – прописными буквами латинского алфавита S.

1.2.2. Символы, обозначающие отношение между

Геометрическими фигурами.

1. º - знак совпадения, тождественности;

(АВ) º (СD) – прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D.

2. @ - знак конгруентности;

ÐАВС @ ÐМNK – угол АВС конгруентен углу МNK.

3. ~ - знак подобности;

D АВС ~ D МNK – треугольники АВС и МNK подобны.

4. || -знакпараллельности;

S || W - плоскость S параллельна плоскости W.

5. ^-знакперпендикулярности;

а ^ b – прямые а и b перпендикулярны.

6. 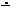- Знак скрещивания;

с 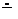d – прямые с и d скрещиваются.

7. = - Знак результата действия, равенства.

8. Î - Знак принадлежности;

А Î ℓ - точка А принадлежит прямой ℓ.

9. ¤- Знак отрицания;

А Ï ℓ - точка А не принадлежит прямой ℓ;

[АВ] ¹ [СD] - отрезок [АВ] не равен отрезку [СD].

10. Ì - Знак включения, содержания (является подмножество);

а Ì S - плоскость S включает в себя линию а или множество точек линии а, является подмножеством точек плоскости S.

11. È - Знак объединение множеств;

АВСD = [АВ] È [ВС] È [СD] - ломаная линия, АВСD есть объединение отрезков [АВ], [ВС], [СD].

12. ∩ - Знак пересечение множеств;

m=S ∩ W - линияm есть результат пересечения плоскости S и W.

1.2.3. Символы, обозначающие логические операции.

1. Ù- Конъюнкция предложений;соответствует союзу «и».

S Ù W = {А : А Î S Ù А Î W} - пересечение поверхностей S и W есть множество точек (линий), состоящее из всех тех и только тех точек А, которые принадлежат как поверхности S, так и поверхности W.

2. Ú- Дизъюнкция предложений; соответствует союзу «или».

3. Þ- Импликация – логическое следствие, означает «если, … то

…».

(ℓ ççс Ù b ççc) Þ ℓ ççb. – Если две прямые линии параллельны третьей прямой, то они параллельны между собой.

4. Û- Эквивалентность. Предложение (ℓ Ûb) понимается в смысле: «если ℓ, то и b; если b, то и ℓ».

5. "- Квантор общности – «для всякого; для всех; для любого».

6. $- Квантор существования, читается: «существует».

7. $1 - Квантор единственности существования, читается:

«существует единственное (-я, -й)».

8. (` )- Отрицание высказывания.

2. ГРАФИЧЕСКАЯ РАБОТА № 1

Задача 1.

Условие. 1. Построить линию пересечения MN плоскости W(DАВС) и Θ(DEDK). Показать видимость пересечения плоскости W(DАВС) с плоскостью Θ(DEDK) в проекциях (рис.4).

2.Определить натуральную величину плоскости W(DАВС) используя способы плоскопараллельного перемещения и вращения (рис. 5, 6).

Запишем условие задачи, используя символы и обозначения.

Дано: W(DАВС) и Θ(DEDK).

Найти: 1. MN = W(DАВС) Ç Θ(DEDK). Видимость W(DАВС) Ç Θ(DEDK) .

2. Н.в. W(DАВС) используя способы плоскопараллельного перемещения и вращения.

Данные для своего варианта взять из таблицы 1.

Таблица 1.

№ вари-анта

хА

уА

zА

xВ

yВ

zВ

xС

yС

zС

xD

yD

zD

xE

yE

zE

xK

yK

zK

Для решения Задачи необходимо изучить следующий теоретический материал [1-17]:

- Образование проекций;

- Точка и прямая. Образование чертежа точки в системе двух и трех плоскостей проекций. Проекции отрезка прямой линии. Положения прямой относительно плоскостей проекций. Точка на прямой. Взаимное положение двух прямых.

- Плоскость. Различные способы задания плоскости на чертеже. Положение плоскости относительно плоскостей проекций. Прямая и точка в плоскости. Прямые особого положения.

- Взаимное положение двух плоскостей, прямой линии и плоскости. Обзор взаимных положений двух плоскостей, прямой линии и плоскости. Пересечение прямой линии с плоскостью. Построение линии пересечения двух плоскостей.

- Способы преобразования чертежа. Основы способа вращения. Вращение точки, отрезка прямой, плоскости вокруг оси, перпендикулярной к плоскости проекций. Применение способа вращения без указания на чертеже осей вращения, перпендикулярных к плоскости П₁ и П₂ (способ плоскопараллельного движения).

Решение.

1.1. В левой половине листа формата А3 (297´420 мм) намечаются оси координат (х, у, z).

Из табл. 1 согласно своего варианта берутся координаты точек А, В, С, D, Е, К вершины треугольников. Для примера рассмотрим построение точки А имеющей значения по координатам Х_А=113, У_А= 83, Z_А=10. Для построения проекций точки А откладываем (рис. 4, а) на оси х от 0 расстояние равное значению абсцисс (Х_А=113) и отмечаем точку А_х. Из полученной точки А_х проводится к оси 0х вертикальная линия проекционной связи.

Линиями проекционной связи называются линии, связывающие пары проекций одной и той же точки и перпендикулярные оси проекций.

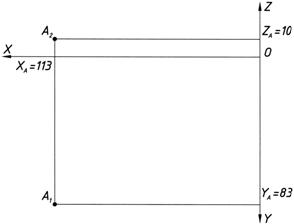
От оси 0х по вертикальной линии проекционной связи от точки А_х вверх откладывается значение Z_А=10 мм, что определяет высоту точки А₂ - фронтальную проекцию точки А, а вниз значение У_А=83 мм, что определяет глубину точки А₁ - горизонтальную проекцию точки А. Аналогично определяются остальные проекции точек плоскостей треугольников В(В₁, В₂), С(С₁, С₂), D(D₁, D₂), …, которые образуют плоскости треугольников W(DАВС) и Θ(DEDK) рис.4,б.

Рис. 4, а	Рис. 4, б

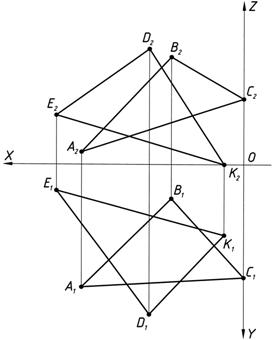
1.2. Известно, что две плоскости треугольников пересекаются по прямой линии. Линию пересечения можно получить с помощью двух точек принадлежащих одновременно обеим плоскостям. В нашем случае мы имеем плоскости общего положения, поэтому введем две вспомогательные секущие плоскости частного положения, поочередно через стороны одного из треугольников.

Через сторону треугольника А₁В₁ (рис. 4в) проводим горизонтально-проецирующую плоскость Г₁. Плоскость Г₁ совпадает со стороной треугольника А₁В₁ (Г₁ºА₁В₁) и пересекает треугольник Θ(DE₁D₁K₁) в точках 1₁, 2₁.

Точка 1₁ лежит на стороне треугольника E₁D₁, а точка 2₁ на стороне E₁K₁. Проекции этих точек 1₂, 2₂ лежат во фронтальной плоскости П₂ на соответствующих проекциях сторон треугольника E₂D₂ и E₂K₂.

Соединив точки 1₂ и 2₂ получаем прямую, которая пересекается со стороной А₂В₂ треугольника W(DА₂В₂С₂) в точке М₂. Горизонтальная проекция точки М - М₁ будет лежать на стороне треугольника А₁В₁. Одна точка искомой прямой линии пересечения треугольников определена.

Аналогично определяем вторую точку прямой пересечения треугольников W(DАВС) и Θ(DEDK) (рис. 4 г). Для этого через сторону треугольника D₂K₂ проводим фронтально-проецирующую плоскость S_2. Плоскость S₂ совпадает со стороной треугольника D₂K₂ (D₂K₂ º S₂) и пересекает треугольник W(DА₂В₂С₂) в точках 3₂, 4₂.

Точка 3₂ лежит на стороне треугольника А₂В₂, а точка 4₂ на стороне А₂С₂. Проекции этих точек 3₁, 4₁ лежат на соответствующих сторонах треугольника W(DА₁В₁С₁) в плоскости проекций П₁. Точка 3₁ лежит на стороне треугольника А₁В₁, точка 4₁ на стороне А₁С₁. Соединяем полученные точки 3₁ и 4₁ между собой прямой линией и получаем отрезок 3₁4₁, который пересекает треугольник Θ(DE₁D₁K₁) по стороне D₁K₁ в точке N₁. Проекция точки N₂ лежит на стороне треугольника D₂K₂.

Рис. 4, в	Рис. 4, г

Запишем алгоритм решения:

М = АВ Ç Θ(DEDK).

АВ Ì Г, Г ^ П₁, А₁В₁ º Г₁.

12 = Г Ç Θ(DEDK), 1₁2₁ º Г₁;

1₁ Î Е₁D₁, 2₁Î E₁K₁,

1₂ Î Е₂D₂, 2₂Î E₂K_2.

1₂È2₂ = 1₂2₂;

М₂ = 1₂2₂ Ç А₂В₂;

М₂ Î А₂В₂, М₁ Î А₁В₁.

Аналогично определяется вторая точка N (рис. 4, г).

N = DK Ç W(DАВС).

DK Ì S, S ^ П₂, D₂K₂ º S₂.

34 = S Ç W(DАВС), 3₂4₂ º S₂;

3₂ Î A₂B₂, 4₂ Î A₂C₂,

3₁ Î A₁B₁, 4₁ Î A₁C₁.

3₁È4₁ = 3₁4₁;

N₁ = 3₁4₁ Ç D₁K₁;

N₁ Î D₁K₁, N₂ Î D₂K₂.

Соединив найденные точки MN (M₁N₁, M₂N₂) получим искомую линию пересечения данных плоскостей (рис. 4, д).

M₁ È N₁ = M₁N₁, M₂ È N₂ = M₂N₂;

W(DАВС) Ç Θ(DEDK) = MN.

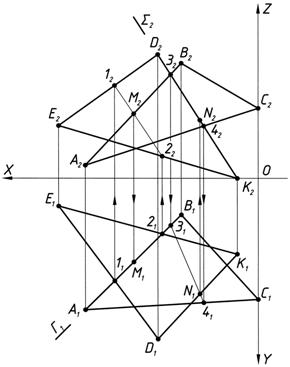
1.3. Определим видимость треугольников W(DАВС) и Θ(DEDK). Для этого используем метод конкурирующих точек. Конкурирующими точками называются такие точки пространства, у которых совпадают какие-либо две одноименные проекции.

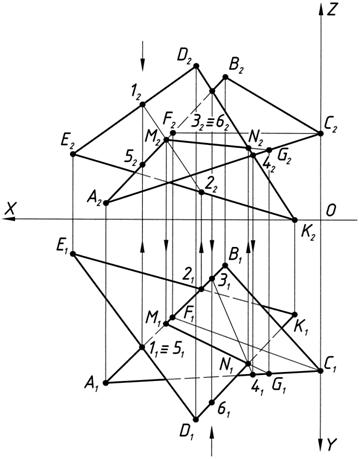
Рис. 4, д

Так, на рис.4, д. показаны конкурирующие точки 1 и 5 (совпадают горизонтальные проекции 1₁ º 5₁) и 3, 6 (совпадают фронтальные проекции 3₂ º 6₂).

Метод конкурирующих точек заключается в определении взаимной видимости точек по их несовпадающим проекциям. Согласно правила большей координаты, точка 1 находится выше точки 5 относительно плоскости П₁ (1₂ > 5₂), поэтому на плоскости П₁ видна точка 1₁, которая закрывает точку 5₁ (считается, что наблюдатель смотрит на плоскость проекций из бесконечности и направление луча зрения параллельно проецирующему лучу s). Таким образом, т.к. точка 1 принадлежащая стороне ЕD плоскости Θ(DEDK), расположена выше точки 5 находящейся на стороне АВ плоскости треугольника W(DАВС), то сторона треугольника Е₁D₁ в горизонтальной плоскости будет видима, а сторона А₁В₁ треугольника АВС от точки 5₁ до точки М₁ будет в горизонтальной плоскости невидима. Видимые линии на чертежах проводятся сплошной контурной линией, а невидимые – тонкой штриховой линией.

На плоскости П₂ видна точка 6, т.к. она находится ближе к наблюдателю (дальше от оси ох в плоскости П₁, 6₁ > 3₁) и закрывает невидимую точку 3. Точка 6₁ расположена на стороне D₁K₁ плоскости Θ(DEDK), в промежутке D₁N₁, и в плоскости П₂ сторона D₂N₂ будет видима и закроет сторону треугольника АВС B₂M₂.

1.4. Для определения натуральной величины плоскости W(DАВС) необходимо преобразовать заданную плоскость общего положения первоначально в положение, проецирующее с использованием способа плоскопараллельного перемещения, как это требуется по условию, а затем проецирующую плоскость в плоскость уровня с использованием способа вращения.

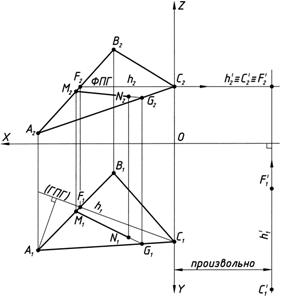
Решение: (для наглядности рассмотрим построения этой задачи на отдельно выполненном чертеже, рис. 5)

1.4.1. В плоскости W(DАВС) (рис. 4, д; 5, а) проводим горизонталь плоскости h = CF.

- Горизонталью плоскости называется прямая h, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций П₁.

-Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости, или если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости.

Согласно определений, для того, чтобы найти горизонталь плоскости, из точки С₂ параллельно оси 0х, проводим фронтальную проекцию горизонтали плоскости (ФПГ) – h₂ (h проведена через точку С, для уменьшения количества точек при построении), и на стороне А₂В₂ плоскости W(DАВС) отмечаем точку F₂, С₂F₂ = h₂. F₁C₁ = h₁ – горизонтальная проекция горизонтали плоскости (ГПГ).

1.4.2. C помощью полученной горизонтали h преобразуем плоскость общего положения в положение фронтально-проецирующей плоскости, используя при этом способ плоскопараллельного перемещения.

Рис. 5, а	Рис. 5, б

Решение задачи способом плоскопараллельного перемещения позволит наиболее удобным образом расположить проекции плоскости на чертеже и избежать наложения проекций, что является важным преимуществом данного способа. Для этого, произвольно, но на расстоянии, превышающем длину перпендикуляра опущенного из точки А₁ до (ГПГ) – h₁ (рис. 5, а), параллельно оси 0у и перпендикулярно к оси 0х, проводим прямую, на которой откладываем длину горизонтали ½h₁ = С₁F₁ú, получая новую горизонтальную проекцию h₁¢= С₁¢F₁¢, где h₁¢ становится фронтально проецирующей прямой, а [С₁F₁] @ [С₁¢F₁¢]. Продолжив линии h₂ и h₁¢ на пересечение, получим проекции точек F₂¢ º C₂¢ º h₂¢ спроецированных в одну точку (рис. 5, а).

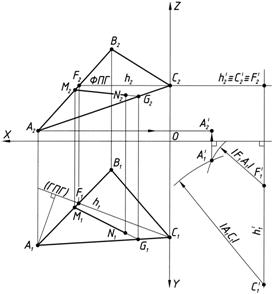
1.4.3. Построение фронтально-проецирующей плоскости начнем с построения ее горизонтальной проекции. Одна из вершин треугольника уже определена эта точка С₁¢. Для того, чтобы определить следующую вершину треугольника, например, точку А₁¢ необходимо в горизонтальной плоскости проекций П₁ DА₁В₁С₁ замерить раствором циркуля величину равную стороне треугольника ½А₁С₁½ и этим значением провести из точки С₁¢ дугой линию (рис. 5, б). Затем замерить величину ½F₁А₁½и из точки F₁¢ провести следующую дугу. В пересечении дуговых линий определится расположение точки А₁¢. Для построения фронтальной проекции точки А¢ необходимо провести горизонтальную линию связи из точки А₂ и вертикальную линию связи из точки А₁¢, в пересечение которых и определяется точка А₂¢.

1.4.4. Аналогично определиться следующая вершина треугольника точка В¢(В₁¢, В₂¢). Соединив в горизонтальной плоскости построенные точки А₁¢В₁¢С₁¢ (рис. 5, в) между собой мы получим горизонтальную проекцию фронтально-проецирующей плоскости, DА₁В₁С₁ @ DА₁¢В₁¢С₁¢. Фронтальная проекция новой плоскости DА₂¢В₂¢С₂¢ должна быть спроецирована в прямую линию и только п