Семестр Начертательная геометрия
Начертательная геометрия
Инженерная графика
Расчетно-графические работы (РГР)
Методические указания для самостоятельной работы студентов
специальностей:
-130400 – Горное дело (специализации: «Открытые горные работы»; «Обогащение полезных ископаемых»; «Подземная разработка рудных месторождений»; «Горные машины и оборудование»; «Электрификация и автоматизация горного производства»);
-190109 - Наземные транспортно-технологические средства (специализация «Подъемно-транспортные, строительные, дорожные средства и оборудование»)
Губкин
УДК 514.18 : 744
М54
Г.И.Фурсова, Начертательная геометрия. Инженерная графика. Расчетно-графические работы (РГР). Методические указания - Губкин, 2011
Методические указания включают: девять расчетно-графических работ (1 семестр) и шесть расчетно-графических работ (2 семестр).
Каждая РГР включает: задание, исходные данные по вариантам, указания по решению и оформлению, пример выполнения, вопросы для самопроверки, рекомендуемую литературу.
Методические указания предназначены в качестве пособия для самостоятельной работы при выполнении расчетно-графических работ по «Начертательной геометрии» (1 семестр) и «Инженерной графике» (2 семестр) для студентов специальностей:
- 130400 – Горное дело (специализации: «Открытые горные работы»; «Обогащение полезных ископаемых»; «Подземная разработка рудных месторождений»; «Горные машины и оборудование»; «Электрификация и автоматизация горного производства»);
- 190109 - Наземные транспортно-технологические средства (специализация «Подъемно-транспортные, строительные, дорожные средства и оборудование»)
Рецензенты:
к.т.н., доцент кафедры ТОММ СТИ НИТУ МИСиС А.В.Александров.
к.т.н., доцент кафедры техники и технологии горного производства Губкинского института (филиала) МГОУ А.А. Паршин.
Под редакцией Г.И.Фурсовой
Губкинский институт (филиал) ФГБОУ ВПО «Московский государственный открытый университет имени В.С. Черномырдина», 2011
© Г.И.Фурсова., 2011
Содержание
Введение 4
Семестр Начертательная геометрия
РГР №1 7
РГР №2 9
РГР №3 10
РГР №4 12
РГР №5 14
РГР №6 16
РГР №7 17
РГР №8 18
РГР №9 21
Вопросы для самопроверки 23
2 семестр Инженерная графика25
РГР №1 28
РГР №2 35
РГР №3 39
РГР №4 39
РГР №5 44
РГР №6 54
Вопросы для самопроверки 64
Литература 65
Введение.
Методические указания по выполнению расчетно-графических работ (РГР) составлены на основании:
Федерального государственного образовательного стандарта высшего профессионального образования специальностей:
- 130400 Горное дело(специализации: «Открытые горные работы»; Обогащение полезных ископаемых»; «Подземная разработка рудных месторождений»; «Горные машины и оборудование»; «Электрификация и автоматизация горного производства»).
- 190109 - Наземные транспортно-технологические средства(специализация «Подъемно-транспортные, строительные, дорожные средства и оборудование»);
Рабочих программ по «Начертательной геометрии, инженерной и компьютерной графике» (специальность 130400) и «Начертательной геометрии и инженерной графике» (специальность 190109);
Учебных планов специальностей:
- 130400 Горное дело(квалификация (степень) «специалист»), (специализации: «Открытые горные работы»; Обогащение полезных ископаемых»; «Подземная разработка рудных месторождений»; «Горные машины и оборудование»; «Электрификация и автоматизация горного производства»).
- 190109 - Наземные транспортно-технологические средства(квалификация (степень) «специалист»), (специализация «Подъемно-транспортные, строительные, дорожные средства и оборудование»);
Дисциплина «Начертательная геометрия, инженерная и компьютерная графика» (специальность 130400), и «Начертательной геометрии и инженерной графике» (специальность 190109) на первом курсе изучается два семестра и состоит из двух структурно и методически согласованных разделов: «Начертательная геометрия», изучаемая в 1 семестре, «Инженерная графика», изучаемая во 2 семестре.
Образец
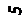

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
Московский государственный открытый университет
имени В.С.Черномырдина
Губкинский институт (филиал)
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Расчетно-графические работы
Выполнил: Студент_____________
Группа ___________
Шифр ______________
Проверил: ____________________
Губкин
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
РГР №1Построить линию пересечения треугольников АВС и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника АВС. Данные для своего варианта взять из табл.1. Пример выполнения приведен на рис.1.
Таблица 1
| № варианта | Размеры и координаты, мм | |||||||||||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | XE | YE | ZE | XK | YK | ZK | |
Указания к решению РГР 1. В левой половине листа формата А3 (297х420м) намечаются оси координат и из табл.1 согласно своему варианту берутся координаты точек А, В, С, D, E, K вершин треугольника (рис.1). Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями. Линии пересечения треугольников строятся по точкам пересечения сторон одного треугольника с другим или по точкам пересечения каждой из сторон одного треугольника с другим порознь. Такую линию можно построить, используя и вспомогательные секущие проецирующие плоскости.
Видимость сторон треугольника определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными толстыми линиями, невидимые следует показать штриховыми линиями. Определяется натуральная величина треугольника АВС.
Плоскопараллельным перемещением треугольник АВС приводится в положение проецирующей плоскости и далее вращением вокруг проецирующей прямой в положение, когда он будет параллелен плоскости проекций.

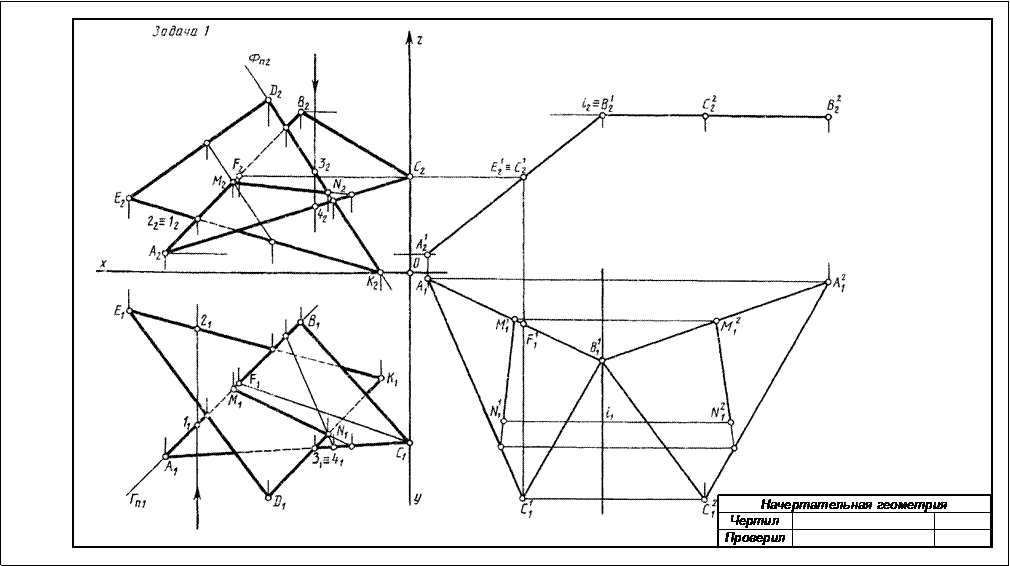
Рис.1
РГР №2 Построить проекции пирамиды, основанием которой является треугольник АВС, а ребро SА определяет высоту h пирамиды. Данные для своего варианта взять из табл.2. Пример выполнения см. на рис.2.
Таблица 2
| № варианта | Координаты и размеры, мм | |||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | h | |
Указания к решению РГР 2. В левой половине листа формата А3 намечаются оси координат и из табл.2 согласно своему варианту берутся координаты точек А, В и С вершин треугольника АВС. По координатам строится треугольник в проекциях. В точке А восставляется перпендикуляр к плоскости треугольника и на нем выше этой плоскости откладывается отрезок АS, равный заданной величине h. Строятся ребра пирамиды. Способом конкурирующих точек определяется их видимость. Видимые ребра пирамиды следует показать сплошными толстыми линиями, невидимые – штриховыми линиями. Все вспомогательные построения необходимо сохранить на эпюре и показать их тонкими сплошными линиями.
РГР №3Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из табл.3. Пример выполнения см. на рис.2.
Таблица 3
| № варианта | Координаты и размеры, мм | ||||||||||||||||||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | XE | YE | ZE | XK | YK | ZK | XG | YG | ZG | XU | YU | ZU | h | |
Указания к решению РГР 3. В оставшейся правой половине листа формата А3 намечаются оси координат и из табл.3 согласно своему варианту берутся координаты точек А, В, С и D вершин пирамиды и координаты точек Е, К, G и U вершин многоугольника нижнего основания призмы, а также высота h призмы. По этим данным строятся проекции многогранников (пирамида и призма). Призма своим основанием стоит на плоскости уровня, горизонтальные проекции ее вертикальных ребер преобразуются в точки. Грани боковой поверхности призмы представляют собой отсеки горизонтально проецирующих плоскостей.
Линии пересечения многогранников определяются по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линии пересечения граней многогранника. Соединяя каждые пары таких точек одних и тех же граней отрезками прямых, получаем линию пересечения многогранников.
Видимыми являются только те стороны многоугольника пересечения, которые принадлежат видимым граням многогранников. Их следует показать сплошными толстыми линиями, невидимые отрезки пространственной ломаной показать штриховыми линиями.
Задаче уделить особое внимание. Все построения на чертеже тщательно проверить. Допущенные ошибки приводят к неправильному решению следующей РГР – РГР № 4 (построение развертки многогранников).


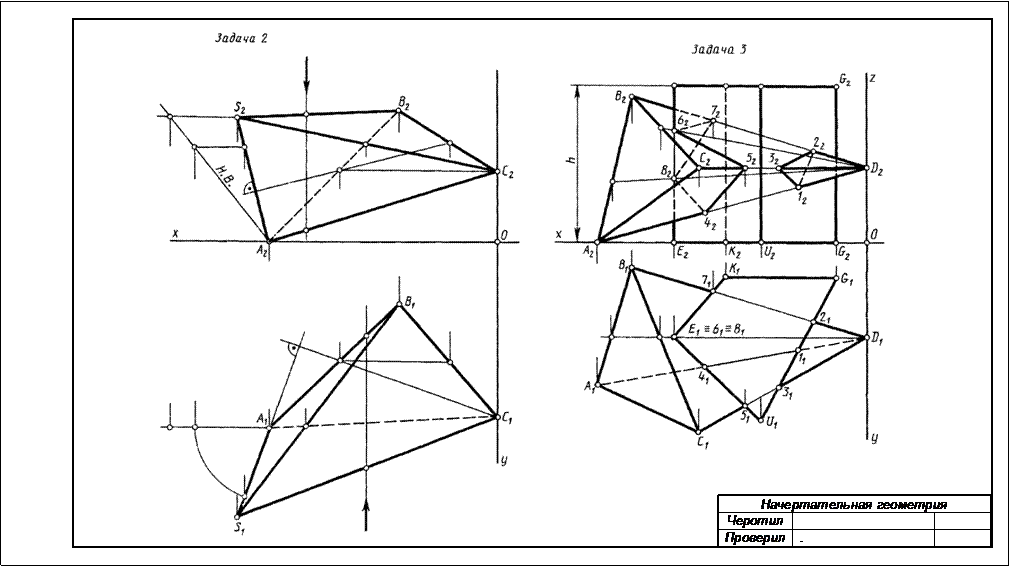
Рис.2
РГР №4Построить развертки пересекающихся многогранников – прямой призмы с пирамидой. Показать на развертках линию их пересечения. Пример выполнения приведен на рис.3.
Указания к решению РГР 4. Чтобы решить данную задачу, следует перевести на кальку формата 297х420мм чертеж пересекающихся многогранников с задачи 3. Здесь же выполнить вспомогательные построения для определения натуральных величин ребер многогранников.
На листе бумаги ватман формата А3 (297х420мм) строятся развертки многогранников.
Развертка прямой призмы. Для построения развертки прямой призмы поступают следующим образом:
а) проводят горизонтальную прямую;
б) от произвольной точки G этой прямой откладывают отрезки GU, UE, EK, KG, равные длинам сторон основания призмы;
в) из точек G, U, … восставляют перпендикуляры и на них откладывают величины, равные высоте призмы. Полученные точки соединяют прямой. Прямоугольник GG1G1G является разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, E, K восставляют перпендикуляры;
г) для получения полной развертки поверхности призмы к развертке поверхности пристраивают многоугольники ее оснований.
Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломаных линий 1 2 3 и 4 5 6 7 8 пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке поступаем так: на отрезке GU от точки G вправо откладываем отрезок G10, равный отрезку G1 (рис.3).
Из точки 10 восставляем перпендикуляр к отрезку GU и на нем откладываем аппликату z точки 1. Аналогично строят и находят остальные точки.
Развертка пирамиды. На кальке определяют натуральную величину каждого из ребер пирамиды. Зная натуральные величины ребер пирамиды, строят ее развертку. Определяют последовательно натуральные величины граней пирамиды. На ребрах и на гранях пирамиды (на развертке) определяют вершины пространственной ломанной пересечения пирамиды с призмой.
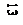

Рис.3
РГР №5Построить в плоскости АВС проекции окружности заданного радиуса R с центром в точке А. Данные для своего варианта взять из табл.4. Пример выполнения чертежа приведен на рис.4.
Таблица 4
| № варианта | Координаты и размеры, мм | |||||||||
| XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | R | |
Указания к решению РГР № 5. В левой трети листа формата А3 (297х420мм) намечают оси координат и из табл.4 согласно своему варианту берутся координаты точек А, В и С, определяющие плоскость окружности с центром в точке А и заданного радиуса R (рис.4). На основные плоскости проекций П1 и П2 окружность проецируется в виде эллипсов. В горизонтальной плоскости проекций П1 и П2 большая ось 12 эллипса совпадает с проекцией направления горизонтали плоскости и равна 2R – диаметру окружности; малая ось равна ортогональной проекции того диаметра окружности, который определяет наибольший угол наклона плоскости окружности к плоскости проекций П1.
Построение малой оси может быть выполнено следующим образом. Отметим в горизонтальной плоскости проекций соответственно полухорды 35 и 56 эллипса и окружности. Полухорду 56 вращением вокруг точки 5 совместим с большой осью. В совмещенном положении она равна отрезку 57. Точки 3 и 7 соединяем прямой линией. Из точки 2 проведем прямую, параллельную прямой 37, до пересечения в точке 8 с направлением малой оси эллипса. Отрезок А181 определяет величину малой полуоси эллипса – горизонтальной проекции окружности.
Во фронтальной плоскости проекции П1 и П2 большая ось эллипса 3242 совпадает с направлением фронтали плоскости и равна 2R – диаметру окружности; малая ось равна ортогональной проекции того диаметра окружности, который определяет наибольший угол наклона плоскости окружности к плоскости проекций П1 и П2. Малая ось эллипса на фронтальной плоскости проекций определяется построением, аналогичным выполненному в горизонтальной плоскости проекций.
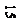

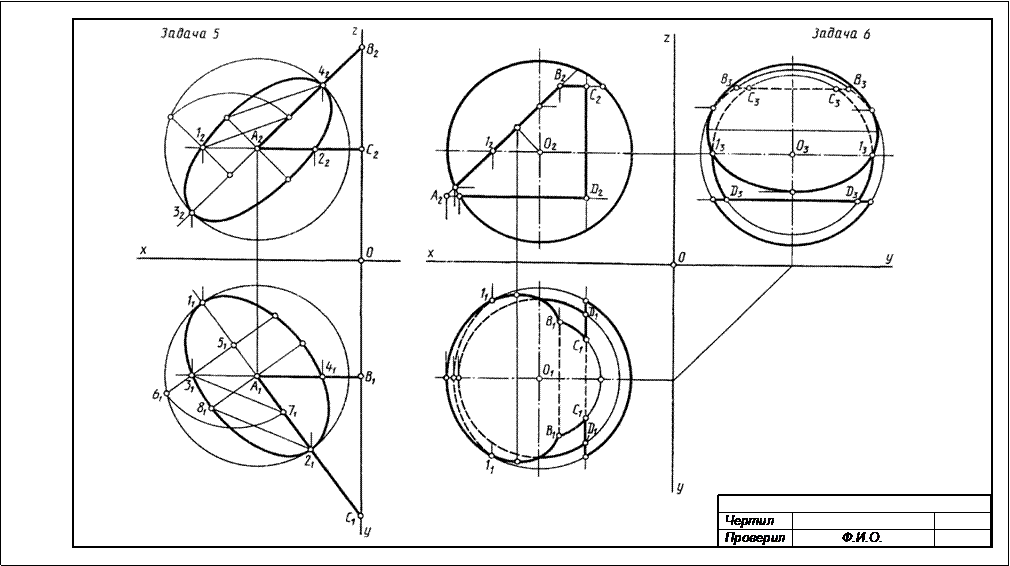
Рис.4
РГР №6На трехпроекционном чертеже построить недостающие проекции сквозного отверстия в сфере заданного радиуса R. Вырожденная (фронтальная) проекция сквозного отверстия представлена четырехугольником: координаты проекций точек А, В, С и D вершин четырехугольника – сквозного отверстия на сфере – известны (табл.5). Пример выполнения приведен на рис.4
Таблица 5
| № варианта | Координаты и размеры, мм | |||||||||||||||
| XО | YО | ZО | XА | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | R | |
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - | |||||||||||||
| - | - | - | - |
Указание к решению РГР № 6. Намечаются оси координат с началом координат в центре листа формата А3. Строятся проекции сферы заданного радиуса R с центром в точке О. Определяются по заданным координатам (табл.4) проекции точек А, В, С и D (вершин четырехугольника) сквозного отверстия на сфере и строится многоугольник – вырожденная проекция линии сквозного отверстия. Далее задача сводится к определению недостающих проекций точек поверхности сферы.
Вначале определяются характерные точки линии сквозного отверстия: точки на экваторе, главном меридиане, наиболее удаленные и ближайшие точки поверхности сферы к плоскостям проекций.
РГР №7Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные проецирующие скрещивающиеся прямые. Данные для своего варианта взять из табл.6 Пример выполнения приведен на рис.5
Таблица 7
| № варианта | Координаты и размеры, мм | ||||||||
| XК | YК | ZК | R | h | XЕ | YЕ | ZЕ | R1 | |
Указания к решению РГР №7.В правой половине листа намечают оси координат и из табл.4 берут согласно своему варианту величины, которыми задаются поверхности конуса вращения и цилиндра вращения. Определяют центр (точка К) окружности радиуса R основания конуса вращения в горизонтальной координатной плоскости. На вертикальной оси на расстоянии h от плоскости уровня и выше ее определяют вершину конуса вращения.
Осью цилиндра вращения является фронтально-проецирующая прямая точки Е; основаниями цилиндра являются окружности радиуса R1. Образующие цилиндра имеют длину, равную 3R1, и делятся пополам фронтальной меридиональной плоскостью конуса вращения.
С помощью вспомогательных секущих плоскостей определяют точки пересечения очерковых образующих одной поверхности с другой и промежуточные точки линии пересечения поверхностей. Проводя вспомогательную секущую фронтальную меридиональную плоскость конуса вращения, определяют точки пересечения главного меридиана (очерковых образующих) конуса вращения с параллелью (окружностью) проецирующего цилиндра. Выбирая горизонтальную секущую плоскость, проходящую через ось цилиндра вращения, определяют две точки пересечения очерковых образующих цилиндра с поверхностью конуса.
Высшую и низшую, а также промежуточные точки линии пересечения поверхности находят с помощью вспомогательных горизонтальных плоскостей – плоскостей уровня. По точкам строят линию пересечения поверхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.
РГР №8Построить развертки пересекающихся цилиндра вращения с конусом вращения. Показать на развертках линии их пересечения. Чертеж-задание для чертежа получить, переведя на кальку формата А3 (297х420мм) чертеж пересекающихся поверхностей с РГР 7. Пример выполнения приведен на рис.6
Указания к решению РГР 8. На листе бумаги ватмана формата А3 (297х420мм) строят развертки поверхностей.
Развертка цилиндра вращения. Выбирают горизонтальную прямую линию и не ней спрямляют линию нормального сечения цилиндра вращения - окружность радиуса R1. строят развертку боковой поверхности цилиндра. На развертке помечают прямолинейные образующие, проходящие через характерные точки пересечения цилиндра с конусом. Эти точки отмечают на соответствующих образующих. Они определяют линию пересечения поверхностей развертки. Полная развертка цилиндра вращения представляется разверткой его боковой поверхности и основаниями – окружностями радиуса R1.
Развертка конуса вращения. Разверткой поверхности конуса вращения является круговой сектор с углом a=R/(L∙360), где R – радиус окружности основания конуса вращения; L – длина образующей.
На развертке конуса вращения строят прямолинейные образующие или параллели, проходящие через характерные точки линий пересечения конуса вращения с цилиндром вращения. Через такие точки проходят линии пересечения поверхностей в преобразовании (на развертке).
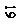

Рис.5
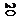

Рис.6
РГР №9 Построить линию пересечения фронтально-проецирующего цилиндра вращения с поверхностью открытого тора (кольцо). Данные для своего варианта взять из табл.7. Пример выполнения см. на рис.7.
Таблица 7
| № варианта | Координаты и размеры, мм | |||||||
| XК | YК | ZК | R1 | XЕ | YЕ | ZЕ | r | |
Указания к решению РГР №9В <
