Взаимное положение прямых в пространстве.
Прямые в пространстве могут быть параллельны могут пересекаться или скрещиваться.
Параллельные прямые — если прямые в пространстве параллельны, то параллельны и их параллельные проекции.
Пересекающиеся прямые — это прямые имеющие общую точку.
На эпюре пересекающихся прямых, точки пересечения фронтальных и горизонтальных проекций лежат на одной линии связи.
Скрещивающиеся прямые — это прямые которые не параллельны и не пересекаются.
На эпюре точки пересечения фронтальных и горизонтальных поверхностей, не лежат на одном уровне связи.
Со скрещивающимися прямыми связано такое понятие как конкурирующие точки.
Конкурирующие точки — это точки лежащие на одном проецирующем луче.
Взаимное положение прямой и точки. Деление отрезка в данном отношении.
Взаимное положение прямой точки
Точка принадлежит прямой в пространстве если все её проекции принадлежат одноименным проекциям данной прямой.
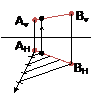 Деление отрезка в данном отношении
Деление отрезка в данном отношении
Разделить отрезок АВ
в отношении 1:4.
Проецирование плоских углов. Теорема о проецировании прямого угла.
Две пересекающиеся прямые образуют плоский угол. Если обе стороны плоского угла параллельны, какой либо плоскости проекции, то его проекция на эту плоскость равна самому плоскому углу. Если плоскость в которой содержится некоторый плоский угол перпендикулярно плоскости проекции, то данный угол проецируется на её виде прямой линии. Исключение составляет прямой угол.
Теорема о проецировании прямого угла
Если плоскость прямого угла не перпендикулярна плоскости проекции и хотя бы одна его сторона параллельна этой плоскости, то данный угол проецируется на рассматриваемую плоскость проекции в виде прямого угла.
Плоскость. Задание плоскости на эпюре. Положение относительно плоскостей проекции. Собирательное свойство следа проецирующей плоскости.
Способы задания плоскости на эпюре:
1. Проекциями трёх точек не лежащими на одной прямой.
2. Проекции прямой и точки не принадлежащие этой прямой.
3. Проекции двух пересекающихся прямых.
4. Проекции двух параллельных прямых.
5. Проекциями любой плоской фигуры.
6. Следами:
Следом плоскости называется прямая линия которой плоскость пересекает плоскость проекции.
Положение плоскости относительно плоскостей проекции.
1. Плоскость общего положения — это плоскость расположенная наклонно ко всем плоскостям проекции.
2. Проецирующей плоскостью — это плоскости перпендикулярны какой-либо плоскости проекции.
а) Горизонтально проецирующая плоскость — перпендикулярно плоскости горизонтальной плоскости проекции.
б) Фронтально проецирующая плоскость — это плоскость перпендикулярна фронтальной плоскости проекции.
в) Профильно-проецирующая плоскость — это плоскость перпендикулярная профильной плоскости проекции.
3) плоскость уровня — это плоскости параллельные какой либо плоскости проекции и перпендикулярные двум другим.
а) Горизонтальная плоскость уровня — это плоскость параллельная горизонтальной плоскости проекции.
б) Фронтальноа плоскость уровня — это плоскость параллельная фронтальной плоскости проекции.
в) Профильная плоскость проекции — её натуральная величина параллельна профильной плоскости проекции.
Собирательное свойство следа проецирующей плоскости.
Любая фигура принадлежащая проецирующей плоскости отображается (или проецируются) на соответствующей след этой плоскости.
Плоскость уровня через прямую общего положения провести нельзя. Такую плоскость можно провести только через соответствующую прямую уровня, например через горизонталь горизонтальную плоскость уровня, через фронталь фронтальную.
10. Прямая и точка в плоскости (Принадлежность прямой и точки плоскости).
Прямая принадлежит плоскости:
1) Если первая проходит через две точки лежащие в этой плоскости.
2) Если проходит через точку лежащую в этой плоскости параллельно любой прямой принадлежащей в этой плоскости.
Признак принадлежности плоскости:
Точка принадлежит плоскости если лежит на прямой принадлежащей этой плоскости.
