Разные задачи на четырехугольники

Пример 4. Через данную точку внутри угла проведите прямую, отрезок которой, заключенный внутри этого угла, делился бы данной точкой пополам.

Решение. Внутри угла с вершиной 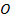дана точка 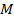. Изобразим это на Рис. 12 со всеми элементами, которые понадобятся нам для решения задачи.

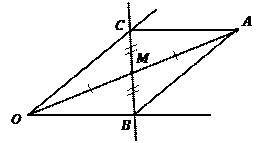
Рис. 12

Отложим отрезок 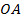из точки 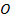через точку 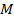так, чтобы 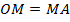, затем проведем отрезки 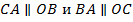, получим точки пересечения со сторонами угла 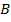и 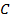соответственно. Соединим эти точки прямой, она и будет искомой. Докажем это.

Построенная фигура 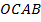является параллелограммом, т.к. по построению имеет параллельные противоположные стороны, отрезки 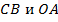являются диагоналями параллелограмма, следовательно, по его свойству точкой пересечения ( 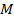) делятся пополам и 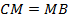, что и требовалось по условию задачи.

Ответ. Искомая прямая – .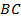

Пример 5. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Найдите стороны прямоугольника.

Решение. Изобразим Рис. 13.

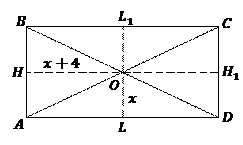
Рис. 13

Опустим из точки пересечения диагоналей перпендикуляры на стороны, длины которых и будут расстояниями от точки пересечения диагоналей до сторон прямоугольника. Обозначим отрезок 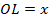, тогда по условию 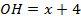. Поскольку 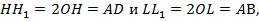получаем, что 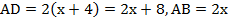. Подставим это в формулу периметра прямоугольника:

.

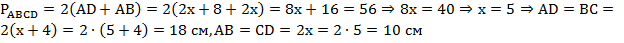Ответ: .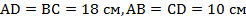

Сегодня мы повторили и закрепили знания по теме «параллелограммы».

Домашнее задание

1. В ромбе одна из диагоналей равна стороне. Определить углы ромба.

2. В прямоугольном треугольнике прямой угол разделён пополам; из точки пересечения биссектрисы и гипотенузы проведены прямые, параллельные катетам. Доказать, что четырёхугольник, образованный этими прямыми и катетами, есть квадрат.

3. Построить квадрат по диагонали.

Урок 13: Контрольная работа.

1 вариант

1.а) Периметр ромба равен 40 см, а один из его углов равен 60º. Найдите длину диагонали, противолежащей этому углу.

б) Периметр прямоугольника равен 46 см, а одна из его сторон больше другой стороны на 4 см. Найдите стороны прямоугольника.

в) Сумма двух сторон прямоугольника равна 24 см, а периметр – 56 см. Найдите стороны прямоугольника.

2.а) Один из углов параллелограмма 40º. Найдите все углы параллелограмма.

б) Один из углов параллелограмма на 50º меньше другого. Найдите все углы параллелограмма.

в) Угол между высотами параллелограмма, проведенными из одной вершины, равен 125º. Найдите углы параллелограмма.

3.а) В четырехугольнике АВСД, проведена диагональ АС, ÐАСВ = ÐСАД, ÐАСД = ÐСАВ. Доказать, что четырехугольник АВСД – параллелограмм.

б) AKCF – параллелограмм, B є KC; D є AF; KB = DF. Доказать, что ABCD – параллелограмм.

в) Доказать, что биссектрисы двух противолежащих углов параллелограмма параллельны.

2 вариант

1.а) Один из углов ромба равен 120º, а диагональ, исходящая из вершины этого угла, равна 10 см. Найдите периметр ромба.

б) Периметр прямоугольника равен 63 см, а одна из его сторон больше другой стороны в 2 раза. Найдите стороны прямоугольника.

в) Полупериметр прямоугольника равен 26 см, а сумма двух сторон – 22 см. Найдите стороны прямоугольника.

2.а) Один из углов параллелограмма 120º. Найдите все углы параллелограмма.

б) Один из углов параллелограмма в 3 раза больше другого. Найдите все углы параллелограмма.

в) Из вершины одного угла параллелограмма проведены биссектриса этого угла и высота. Угол между ними равен 30º. Найдите углы параллелограмма.

3.а) В четырехугольнике АВСД проведена диагональ ВД, ÐСВД = ÐАДВ, ÐАВД = ÐВДС. Доказать, что четырехугольник АВСД – параллелограмм.

б) ALCE – параллелограмм, L є AB; E є CD; BL = DE. Доказать, что ABCD – параллелограмм.

в) Дан прямоугольник ABCD. К его диагонали BD проведены перпендикуляры AM и CN. Точки M и N соединены соответственно с точками C и A. Доказать, что четырехугольник AMCN – параллелограмм.

Примечание: данная контрольная работа разноуровневая, в каждом номере (№1,2, или 3) своего варианта нужно сделать только одно из заданий под буквой а), б) или в). Задания под буквой а) оцениваются в 2 балла; под буквой б) – 3 балла; под буквой в) – 4 балла. Каждый из вас может выбрать себе задание по силам. Удачи!