Задачи с прямоугольниками, вписанными в треугольники

Пример 5. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.

Решение. Изобразим Рис. 8. Ясно, что можно построить множество различных прямоугольников, вписанных в прямоугольный треугольник, но выясняется, что их периметры будут одинаковы, покажем это и найдем искомый периметр.

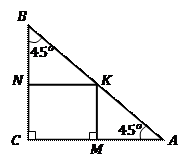
Рис. 8

По условию 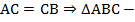равнобедренный .

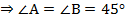Искомый периметр прямоугольника: .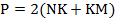

Рассмотрим прямоугольный : .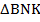

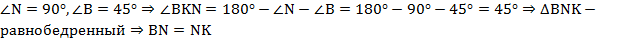Тогда периметр прямоугольника : .

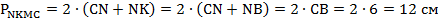Ответ: 12 см.

Пример 6. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны и периметр прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см?

Решение. Изобразим Рис. 9 и укажем на нем все элементы, которые мы введем в процессе решения задачи.

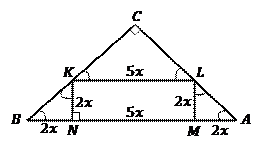
Рис. 9

По условию 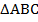равнобедренный и прямоугольный .

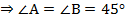Указано, что вписанный прямоугольник имеет заданные пропорции, поэтому его стороны можно ввести, как определенное количество неизвестных нам частей : .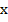

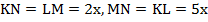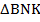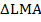Рассмотрим треугольники и – они прямоугольные и имеют по одному углу 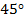, следовательно, второй угол у них тоже по 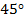(см. решение предыдущей задачи), т.е. они равнобедренные, и .

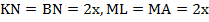Теперь можем выписать длину гипотенузы 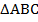как сумму длин отрезков, на которые она разбита вписанным прямоугольником (через те части 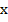, которые мы ввели): .

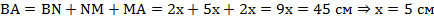Теперь можем посчитать длины сторон прямоугольника и его периметр: .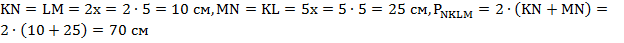

Ответ: стороны равны .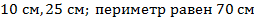

Сегодня мы рассмотрели прямоугольник, его свойства, признаки и задачи на прямоугольник. На следующем уроке мы познакомимся с такими частными случаями параллелограмма, как ромб и квадрат.

Домашнее задание

1. В прямоугольнике диагональ образует со стороной угол, равный 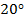. Определить угол между диагоналями, обращенный к меньшей стороне.

2. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр этого прямоугольника равен 56 см. Определить его стороны.

3. Построить прямоугольник по основанию, равному 2,4 см, и диагонали, равной 3,1 см.

Урок 11: Ромб и квадрат.

На этом уроке пришло время познакомиться с ещё двумя видами параллелограмма: ромбом и квадратом. С этими фигурами каждый из нас знаком с самого детства, однако мало кто ассоциирует их с параллелограммом. А их свойства многие из нас применяли на практике, не зная даже, на чём они основаны. Мы рассмотрим определения и свойства параллелограмма и квадрата, а также решим несколько задач с использованием указанных свойств.

Ромб и его свойства

Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма. Однако есть и специфические свойства, о которых пойдёт речь. Но для начала сформулируем одно из определений ромба.

Ромб –это параллелограмм, у которого все стороны равны.

Сформулируем и докажем теорему о свойствах ромба.

Теорема

Диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов) (см. Рис. 1).

Дано:

– ромб

Доказать:

.

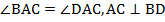Доказательство:

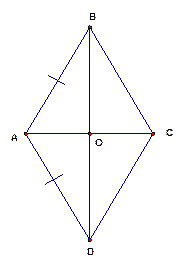
Рис. 1

Рассмотрим 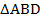: 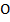– середина 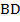(так как ромб является параллелограммом, то его диагонали в точке пересечения делятся пополам). Кроме того, из определения ромба следует, что 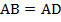. Значит, треугольник 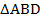– равнобедренный; 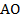является медианой этого треугольника, проведённой к основанию, а, значит, и биссектрисой, и высотой. Из этого следует, что:

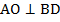, то есть диагонали ромба перпендикулярны;

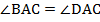, то есть диагонали ромба являются биссектрисами его углов (равенство остальных углов можно доказать аналогично).

Доказано.

Ещё один частный случай параллелограмма – квадрат.

Квадрат и его свойства

Квадрат –это прямоугольник, у которого все стороны равны.

Квадрат обладает всеми свойствами прямоугольника и ромба. А именно:

· все углы квадрата прямые;

· диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делят углы квадрата пополам.

Задачи на ромб и квадрат

Теперь рассмотрим несколько задач, в которых встречаются ромб и квадрат.

Задача 1.

В ромбе одна из диагоналей равна стороне (см. Рис. 2). Найти:

а) углы ромба;

б) углы между диагоналями и сторонами.

Дано: – ромб; .

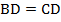Найти: а) 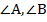; б) .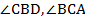

Решение:

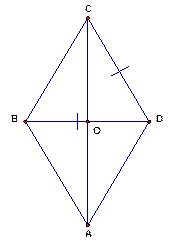
Рис. 2

а) 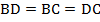(так как у ромба все стороны равны). Значит, треугольник 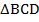– равносторонний. Отсюда следует, что угол 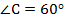. Так как в любом параллелограмме сумма соседних углов равна 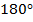, то .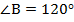

Ответ: .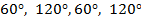

б) По доказанной выше теореме: 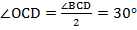. Аналогично получаем, что .

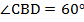Ответ: .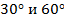

Задача 2.

Найти периметр ромба , в котором 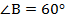, а меньшая диагональ равна 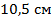. Найти периметр ромба.

Дано: – ромб; .

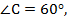
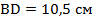Найти: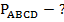

Решение:

Рис. 3

Рассмотрим треугольник 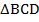, в нём: 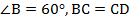. Значит, данный треугольник равнобедренный, угол при вершине у него равен 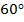, два других угла при основании равны, поэтому данный треугольник – равносторонний. Значит: 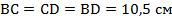. Так как в ромбе все стороны равны, то периметр ромба равен: .

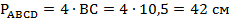Ответ: .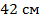

Задача 3.

Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен .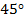

Дано: – ромб, .

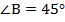Найти: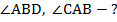

Решение:

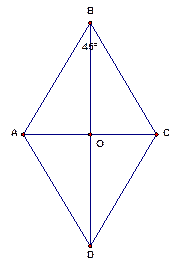
Рис. 4

Вспомним, что в любом параллелограмме противоположные углы, а сумма углов, прилежащих к одной стороне, равна 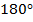. Из этого следует, что: 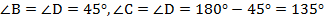. Теперь воспользуемся доказанной вначале теоремой: .

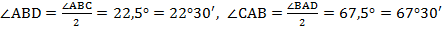Ответ: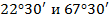

Задача 4.

Докажите, что параллелограмм является ромбом, если:

а) его диагонали взаимно перпендикулярны;

б) его диагонали являются биссектрисами углов.

а) Дано: – параллелограмм, .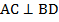

Доказать: – ромб.

Доказательство:

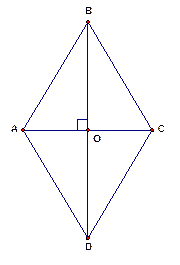
Рис. 5

Рассмотрим треугольник 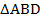: в нем 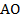является одновременно и высотой (так как диагонали перпендикулярны), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, 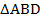– равнобедренный. Из этого следует, что: 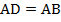. Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: 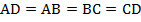. То есть – ромб.

Доказано.

б) Дано: – параллелограмм, 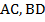– биссектрисы углов параллелограмма.

Доказать: – ромб.

Доказательство:

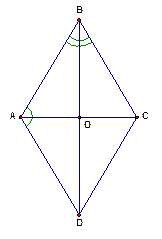
Рис. 6

Рассмотрим треугольник 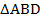: в нем 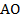является одновременно и биссектрисой (так как диагонали являются биссектрисами углов), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, 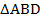– равнобедренный. Из этого следует, что: 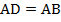. Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: 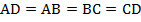. То есть, – ромб.

Доказано.

Задача 5.

Докажите, что ромб, у которого один из углов прямой, является квадратом.

Дано: – ромб,

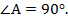
Доказать: – квадрат.

Доказательство:

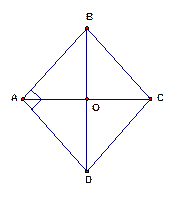
Рис. 7

Вспомним, что квадрат – это одновременно прямоугольник и ромб. Если говорить о сформулированном строгом определении, то квадрат – это прямоугольник, у которого все стороны равны. Равенство сторон следует из того, что данный четырёхугольник – ромб. Осталось доказать, что он является ещё и прямоугольником. По условию: 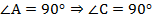(у любого параллелограмма противоположные углы равны). Кроме того, сумма соседних углов параллелограмма равна 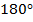. Значит: 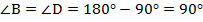. Отсюда мы получаем, что – прямоугольник, а значит, и квадрат.

Доказано.

На этом уроке мы изучили ромб и квадрат, а также рассмотрели их свойства и решили различные задачи, в которых встречаются ромб и квадрат.

На следующем уроке мы обобщим полученные знания о параллелограммах.

Домашнее задание

1. Найти углы ромба, если его сторона образует с диагоналями углы, разность которых равна .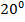

2. Найти углы ромба, если его сторона образует с диагоналями углы, которые относятся как .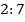

3. Доказать, что прямоугольник, у которого диагонали перпендикулярны, – квадрат.

Урок 12: Повторение теории и решение задач

На этом уроке мы повторим и обобщим все полученные знания при изучении главы «Четырехугольники. Параллелограммы». Вспомним определения, свойства и признаки таких фигур, как параллелограмм, прямоугольник, ромб, квадрат. Решим несколько примеров, которые демонстрируют применение всех изученных фактов к указанным фигурам.