Повторение: определение и свойства параллелограмма

Напомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. То есть, если 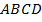– параллелограмм, то 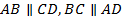(см. Рис. 1).

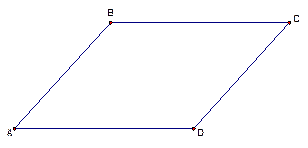
Рис. 1

Параллелограмм обладает целым рядом свойств: противоположные углы равны ( 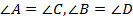), противоположные стороны равны ( 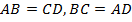). Кроме того, диагонали параллелограмма в точке пересечения делятся пополам, сумма углов, прилежащих к любой стороне параллелограмма, равна 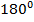и т.д.

Но для того, чтобы пользоваться всеми этими свойствами, необходимо быть абсолютно уверенными в том, что рассматриваемый четырёхугольник – параллелограмм. Для этого и существуют признаки параллелограмма: то есть те факты, из которых можно сделать однозначный вывод, что четырёхугольник является параллелограммом. На предыдущем уроке мы уже рассмотрели два признака. Сейчас рассмотрим третий.

Третий признак параллелограмма и его доказательство

Если в четырёхугольнике диагонали в точке пересечения делятся пополам, то данный четырёхугольник является параллелограммом.

Дано:

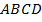– четырёхугольник; ; .

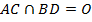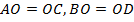Доказать:

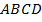– параллелограмм.

Доказательство:

Для того чтобы доказать данный факт, необходимо доказать параллельность сторон параллелограмма. А параллельность прямых чаще всего доказывается через равенство внутренних накрест лежащих углов при этих прямых. Таким образом, напрашивается следующий способ доказательства третьего признака параллелограмма: через равенство треугольников .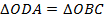

Докажем равенство этих треугольников. Действительно, из условия следует: 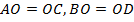. Кроме того, поскольку углы 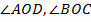– вертикальные, то они равны. То есть:

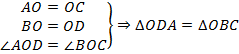(первый признак равенства треугольников – по двум сторонам и углу между ними).

Из равенства треугольников: 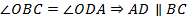(так как равны внутренние накрест лежащие углы при этих прямых и секущей 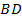). Кроме того, из равенства треугольников следует, что 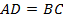. Значит, мы получили, что в четырёхугольнике две стороны равны и параллельны. По первому признаку параллелограмма: 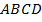– параллелограмм.

Доказано.

Пример задачи на третий признак параллелограмма и обобщение

Рассмотрим пример на применение третьего признака параллелограмма.

Пример 1

Дано:

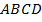–параллелограмм; 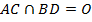. 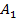– середина 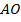, 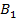– середина 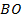, 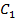– середина 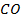, 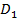– середина 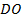(см. Рис. 2).

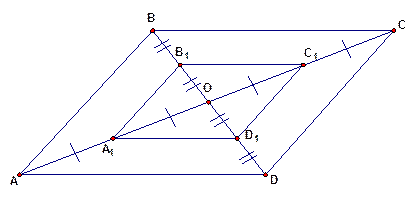
Рис. 2

Доказать: 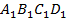– параллелограмм.

Доказательство:

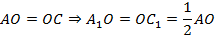
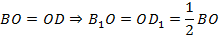
Значит, в четырёхугольнике 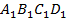диагонали в точке пересечения делятся пополам. По третьему признаку параллелограмма из этого следует, что 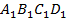– параллелограмм.

Доказано.

Если провести анализ третьего признака параллелограмма, то можно заметить, что этот признак соответствует свойству параллелограмма. То есть, то, что диагонали делятся пополам, является не просто свойством параллелограмма, а его отличительным, характеристическим свойством, по которому его можно выделить из множества четырёхугольников.

На следующем уроке мы рассмотрим решение различных задач про параллелограмм.

Домашнее задание

1. Диагонали четырёхугольника 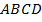пересекаются в точке 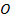. Является ли данный четырёхугольник параллелограммом, если 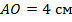, , 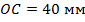, 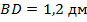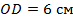. Ответ обоснуйте.

2. Диагонали четырёхугольника 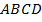пересекаются в точке 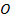. Известно, что 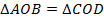. Докажите, что данный четырёхугольник – параллелограмм.

Урок 9: Задачи на параллелограмм.

На уроке мы, прежде всего, повторим уже изученные ранее свойства и признаки параллелограмма и все основные понятия, которые связаны с этой геометрической фигурой. Главной целью занятия будет рассмотрение нескольких примеров на применение знаний о параллелограмме. В процессе решения примеров познакомимся с важнейшей теоремой, связанной с параллельностью прямых, – теоремой Фалеса.

1. Повторение определения, свойств и признака параллелограмма

Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.

Определение. Параллелограмм– четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).

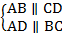
Рис. 1. Параллелограмм

Основные свойства параллелограмма:

Теорема.Первый признак параллелограмма.Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. 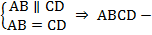параллелограмм.

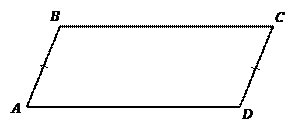
Рис. 2. Первый признак параллелограмма

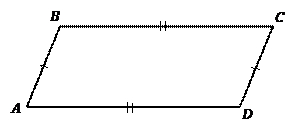
Рис. 3. Второй признак параллелограмма

Теорема. Второй признак параллелограмма.Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник –параллелограмм. 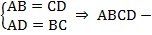параллелограмм.

Теорема. Третий признак параллелограмма.Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. 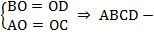параллелограмм.

Рис. 4. Третий признак параллелограмма

Задачи на параллелограммы

Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.

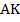Пример 1. В параллелограмме проведены биссектрисы и 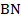, которые пересекаются в точке 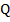. Найти .

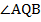Решение. Изобразим Рис. 5.

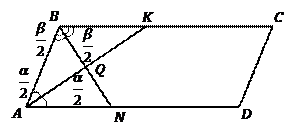
Рис. 5

Обозначим для удобства: 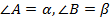. Следовательно, 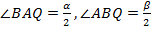поскольку 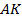и 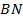биссектрисы.

По теореме о сумме внутренних углов треугольника .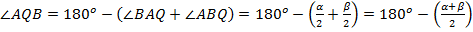

Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: 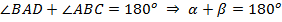. Тогда:

.

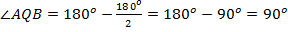Ответ. .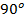

Пример 2. Прямая 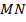, проведенная через середину 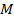стороны 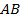параллельно стороне 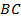треугольника 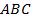пересекает третью его сторону в середине. Доказать, что 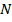– это середина .

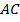Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .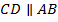

Рис. 6

Рассмотрим четырехугольник :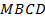

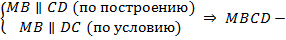параллелограмм по определению. Тогда по свойству равенства противоположных сторон 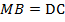, но по условию еще известно, что 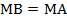, следовательно, .

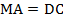Рассмотрим треугольник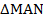и и :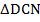

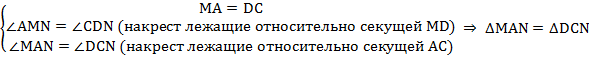по второму признаку равенства треугольников (по стороне и прилежащим углам).

Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что 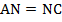. Это означает, что точка 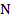является серединой стороны 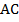. Что и требовалось доказать.

Доказано.

Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях.

Домашнее задание

1. В параллелограмме 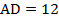см, 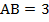см, биссектрисы углов 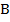и 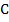пересекают сторону 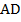в точках 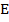и 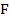. Найдите длину отрезка .

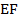2. Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен 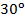. Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.

3. ^* Через середину 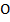диагонали 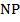параллелограмма 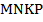проведена прямая, которая пересекает стороны 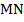и 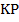в точках 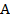и 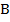соответственно. Докажите, что четырехугольник 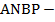параллелограмм.

Урок 10: Прямоугольник

На данном уроке мы будем рассматривать частный случай параллелограмма – прямоугольник. Мы введем его основные свойства, докажем теорему о равенстве диагоналей прямоугольника и сформулируем признак прямоугольника. Затем решим достаточно много задач, которые связаны с этой фигурой.