Тема 1: «Повторение. Четырехугольники. Параллелограммы».

Геометрия.

Тема 1: «Повторение. Четырехугольники. Параллелограммы».

Урок 1: Повторение. Начальные геометрические сведения.

На этом уроке вспомним аксиому о параллельных прямых и следствие из нее. Повторим определение луча и угла и единицы измерения отрезков и углов. Вспомним определение равных геометрических фигур и то, как сравнивают и измеряют отрезки и углы. Вспомним, что такое середина отрезка и биссектриса угла, какие углы называются острыми, прямыми и тупыми. Повторим теоремы о сумме смежных углов и о равенстве вертикальных углов. Вспомним, что такое перпендикулярные прямые и теорему о том, что две перпендикулярные к третьей прямые не пересекаются. И будем решать типовые задачи на повторенный материал.

Повторение начальных геометрических сведений

Вспомним сведения, изученные в текущей теме:

- Аксиома. Через две точки можно провести прямую, и только одну.

- Прямые на плоскости могут пересекаться, могут не иметь общих точек.

- Угол измеряется в градусах. 1 градус – это сто восьмидесятая часть от развернутого угла.

- Сумма смежных углов равна 180^о.

- Вертикальные углы равны между собой.

- Прямые, пересекающиеся под углом 90^о, называются перпендикулярными.

- Прямые, перпендикулярные одной прямой, не пересекаются.

Пример 1

Пример 1: Найти угол между биссектрисами смежных углов.

Решение:

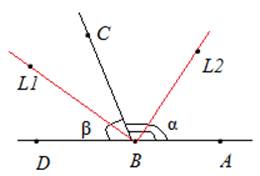
Рис. 1. Чертеж к примеру 1

Биссектриса BL₁ угла DBC = β делит его на два угла, градусная мера которых равна 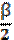. Биссектриса BL₂ угла АBC = α делит его на два угла, градусная мера которых равна 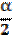. Необходимо найти угол L₁ ВL₂. Выполним сложение углов: L₁ ВL₂ = L₁ ВС + СВL₂ = 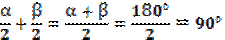. Сумма углов α + β равна 180^о, поскольку данные углы – смежные.

Ответ: 90^о.

Отметим, что в данной задаче нам не было известно, какие градусные меры углов DBC и АBC, однако мы знаем, что их сумма равна 180^о.

Пример 2

Пример 2: Отрезок длиной 36 см поделили на 4 неравных части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей отрезка.

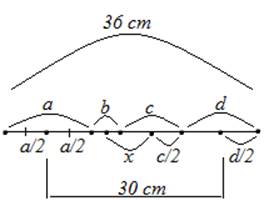
Рис. 2. Чертеж к примеру 2

Решение:

Найдем величину суммы отрезков 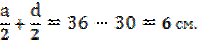Соответственно,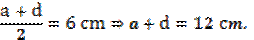

Вычислим сумму длин оставшихся отрезков: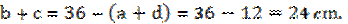

Найдем расстояние между серединами средних частей отрезка.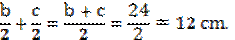

Ответ: 12 см.

Пример 3

Пример 3: Отрезок длиной m разделен на три части. Найти расстояние между серединами крайних частей.

Решение:

Выполним рисунок.

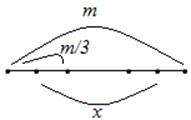
Рис. 3. Чертеж к примеру 3

Поскольку длина трети отрезка равна 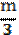, то длина половины этой части равна 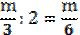. Тогда чтобы найти расстояние между серединами крайних частей, необходимо выполнить действие: .

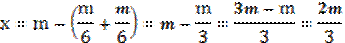Ответ: .

Домашнее задание

1. Определите длину отрезка АВ, если АС : ВС = 3 : 2, а ВС = 3 см.

2. При пересечении прямых образовалось 4 неразвернутых угла. Определите градусные меры этих углов, если сумма трех углов 320^о.

3. Может ли быть такое, что один из смежных углов больше другого в 100 раз?

Урок 2: Повторение. Параллельные прямые и задачи на углы между ними и секущей.

В ходе занятия учащиеся смогут кратко повторить теоретические сведения о параллельных прямых и углах между ними и секущей. Затем применить эти знания, решив несколько задач по соответствующей теме.

Повторение

Задача 1

Задача 1:

Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210 . Найдите эти углы.

Дано: .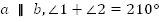

Найти: .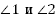

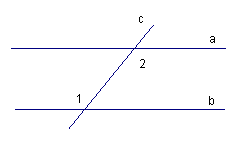
Рис. 5

Решение:

Поскольку прямые a и b параллельны, то накрест лежащие углы равны.

Следовательно, .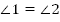

Тогда .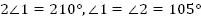

Ответ: .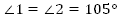

Задача 2

Задача 2:

Найдите все углы, образованные при пересечении параллельных прямых a и b с секущей c, если:

А. один из углов равен ;

Б. один из углов на больше другого.

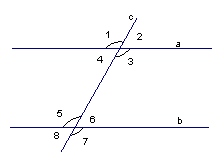
Рис. 6

А.

Дано: .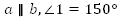

Найти: .

Решение:

1. 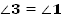(как вертикальные);

2. 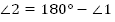(как смежные);

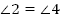(как вертикальные);

;

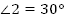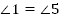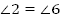3. и (как соответственные)

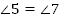и 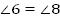(как вертикальные)

Ответ: , .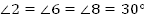

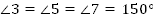Б.

Дано: .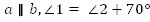

Найти: .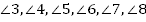

Решение:

1.

+

, .

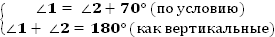
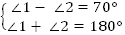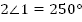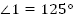Тогда .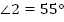

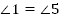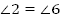2. и (как соответственные)

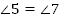и 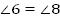(как вертикальные)

Ответ: , .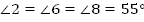

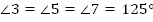Задача 3

Задача 3:

На рисунке 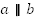, прямые m и n – биссектрисы углов 1 и 2. Докажите, что .

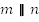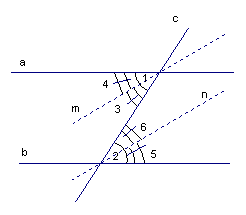
Рис. 7

Доказательство:

Из того, что 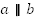, по свойству параллельных прямых вытекает, что .

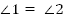Следовательно, углы 3, 4, 5, 6 тоже будут равны между собой, как половинки равных углов.

Тогда из того, что 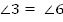, по первому признаку параллельности прямых 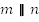, что и требовалось доказать.

Домашнее задание

1. Докажите, что биссектрисы соответственных углов при параллельных прямых параллельны.

2. Две параллельные прямые пересечены третьей прямой так, что сумма двух из полученных восьми углов равна 240 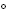. Найдите меры всех образованных углов.

3. Через точку, не лежащую на прямой a, проведено три прямые. Докажите, что по крайней мере две из них пересекают прямую a.

Урок 3: Повторение. Треугольники.

На этом уроке мы повторим основные понятия, пройденные в 7 классе. К ним относятся: важнейшая геометрическая фигура – треугольник, его свойства, признаки равенства треугольников. Для повторения основных фактов, связанных с треугольниками, нам необходимо будет вспомнить понятия, возникающие при рассмотрении пересечения секущей двух параллельных прямых, такие как накрест лежащие, односторонние, соответственные и вертикальные углы. Исходя из этих понятий, мы повторим теоремы о сумме углов треугольника и о внешнем угле треугольника. В ходе урока рассмотрим примеры.

Первый признак равенства треугольников (по углу и прилежащим сторонам) (см. Рис. 1).

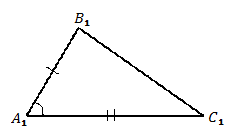
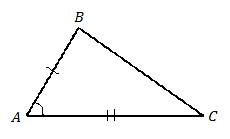
Два треугольника равны, если угол и две прилежащие к нему стороны одного треугольника равны соответственно углу и двум прилежащим к нему сторонам другого треугольника.

.

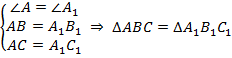Второй признак равенства треугольников (по стороне и прилежащим углам) (см. Рис. 2).

Рис. 2.

Второй признак равенства треугольников

Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника.

.

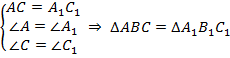Третий признак равенства треугольников (по трем сторонам) (см. Рис. 3).

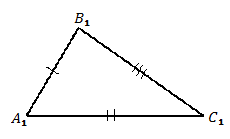
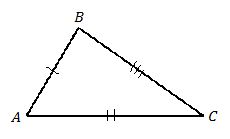
Рис. 3.

Третий признак равенства треугольников

Два треугольника равны, если три стороны одного треугольника равны соответственно трем сторонам другого треугольника.

.

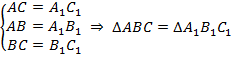Вспомним три признака равенства треугольника: мы можем видеть, что, используя небольшое количество фактов о двух треугольниках, можно получить достаточно много информации о равенстве всех их элементов.

Свойства треугольников, которые мы повторим в дальнейшем, будут связаны со свойствами параллельных прямых.

Пример (признак равенства треугольников по двум сторонам и большему углу)

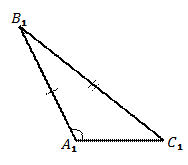
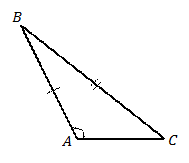
Рис. 8.

Признак равенства треугольников по двум сторонам и большему углу

Два треугольника равны, если две стороны и наибольший угол одного треугольника равны соответственно двум сторонам и наибольшему углу другого треугольника.

.

Доказательство.

Если наибольшим углом окажется угол 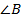, то признак доказан, т.к. он сводится к первому признаку равенства треугольником. Поэтому на Рис. 8 изображен общий случай, когда наибольшим является угол, не лежащий между указанными сторонами, например, это угол 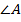. Кстати, наибольший угол 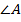не обязательно должен быть тупым, на рисунке так изображено только для наглядности.

Для доказательства равенства треугольников вспомним, что фигуры равны, если их можно совместить.

Мысленно наложим один треугольник поверх второго так, чтобы совпали точк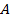и и 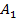. Ввиду равенства сторон 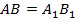и угла 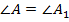несложно представить, что точк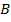и и 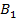тоже совпадут. Получим, что у двух сравниваемых треугольников уже совпали две вершины, но не факт, что совпадет третья ( 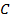и 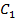), это и осталось доказать.

Докажем этот факт от противного: изобразим исходный треугольник поверх другого треугольника (в скобках указаны совпавшие вершины) и представим, что вершины 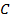и 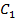не совпали, как это указано на Рис. 9.

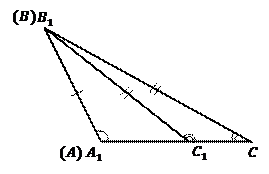
Рис. 9

Нам необходимо доказать, что ситуация несовпадения точек и невозможна.

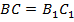Рассмотрим получившейся в результате наложения треугольник . В нем стороны по условию, следовательно, он равнобедренный, следовательно, 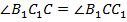. А 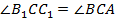, если назвать вершины, как в исходном треугольнике.

Но угол 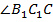является внешним для треугольника 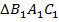, следовательно, 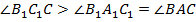. Получили такие соотношения:

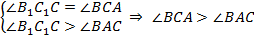, что противоречит условию задачи. Следовательно, точк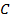и и 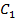совпадают, и .

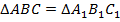Доказано.

В рамках урока мы повторили признаки равенства треугольников и две важнейшие теоремы о треугольниках.

На следующем уроке мы вспомним свойства такого частного вида треугольников, как прямоугольный треугольник.

Домашнее задание

1. На медиане 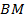треугольника 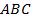отметили точку 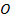так, что 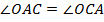. Докажите, что 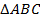– равнобедренный.

2. Равнобедренные треугольник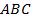и и 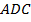имеют общее основание 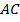. Докажите, что прямая 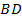– серединный перпендикуляр отрезка .

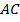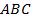
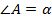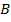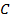3. В треугольнике , биссектрисы внешних углов при вершинах и пересекаются в точке 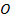. Найдите угол .

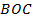4. В треугольнике 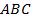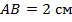, 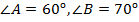. На стороне 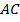отметили точку 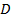так, что 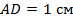. Найдите углы треугольника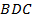

Урок 4: Повторение. Прямоугольные треугольники.

Данный урок посвящен прямоугольным треугольникам и их свойствам. Прямые углы, а значит, и прямоугольные треугольники, встречаются в жизни человека практически на каждом углу (в прямом и переносном смысле). Поэтому изучение их свойств может пригодиться не только при дальнейшем изучении курса геометрии, но и в простых жизненных ситуациях. В 7 классе были изучены самые простые свойства прямоугольных треугольников. Поскольку в 8 классе изучению более сложных свойств будет уделено достаточно большое внимание, необходимо вспомнить то, что нам уже известно про прямоугольные треугольники.

Неравенство треугольника

В любом треугольнике сумма любых двух сторон больше третьей стороны.

Из данного неравенства сразу же следует свойство 3.

Примечание: несмотря на то, что каждый из катетов по отдельности меньше гипотенузы, их сумма оказывается больше. В числовом примере это выглядит так: 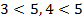, но .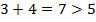

Доказано.

Определение параллелограмма

На прошлом уроке мы рассмотрели понятие выпуклого многоугольника. Теперь изучим частный случай многоугольника – четырехугольник, а точнее – частный случай четырехугольника – параллелограмм.

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны (см. Рис. 1).

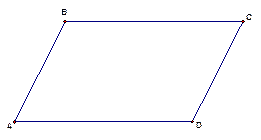
Рис. 1. Параллелограмм

То есть, если даны две параллельные прямые, которые пересекают еще две параллельные прямые, то они образуют фигуру, которая называется параллелограммом .

Из того, что – параллелограмм, можно сделать следующие выводы: 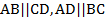. Верно и обратное утверждение: если 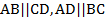, то четырёхугольник – параллелограмм.

Помимо данного определения, можно дать ещё несколько эквивалентных, однако мы остановимся именно на таком, классическом определении параллелограмма, и сформулируем свойства данной фигуры, пользуясь параллельностью её противоположных сторон.

Примеры задач на свойство параллелограмма

Пример 1.

Периметр параллелограмма равен 48 см. Найти его стороны, если одна сторона на 3 сантиметра больше другой (см. Рис. 4).

Дано:

– параллелограмм, . .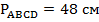

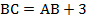Найти:

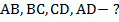
Решение:

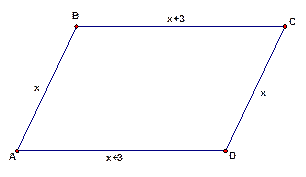
Рис. 4

Обозначим меньшую сторону параллелограмма 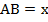. Учитывая свойство 1 для параллелограмма, запишем следующее равенство: 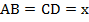. Из условия: .

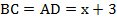Напомним, что периметр многоугольника – это сумма всех его сторон. Поэтому можем записать следующее равенство: .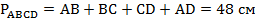

Или: .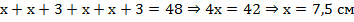

Получаем, что стороны параллелограмма: , .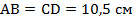

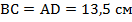Ответ: .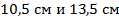

Пример 2

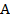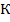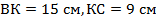Биссектриса угла параллелограмма пересекает сторону в точке . . Найдите периметр параллелограмма.

Дано:

– параллелограмм, 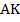– биссектриса. . .

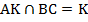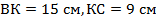Найти:

Решение:

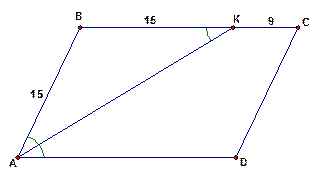
Рис. 5

Вспомним определение биссектрисы: биссектриса делит угол пополам. Это значит, что: . Кроме того, 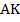является секущей при параллельных прямых 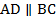. А это значит, что внутренние накрест лежащие углы равны: .

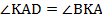Из этого получается:

.

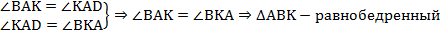Так как 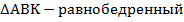, то 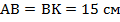. Откуда: .

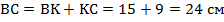Периметр – сумма всех сторон, у параллелограмма противоположные стороны равны. Получаем: .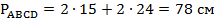

Ответ: .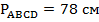

Итак, мы рассмотрели определение и свойства параллелограмма, в частности: равенство противоположных сторон и углов, а также то, что диагонали параллелограмма точкой пересечения делятся пополам, и использовали эти свойства при решении задач.

В дальнейшем мы изучим признаки параллелограмма, а также научимся применять свойства и признаки параллелограмма при решении более сложных примеров.

Домашнее задание

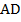1. Найдите периметр параллелограмма , если сторона равна 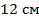и составляет стороны .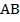

2. Периметр параллелограмма равен 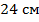. Найдите стороны параллелограмма, если одна из них на 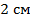больше другой.

3. Найдите углы параллелограмма, если градусные меры двух его углов относятся как .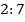

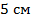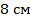4. Точка пересечения диагоналей параллелограмма удалена от двух его вершин на и . Найдите длины диагоналей параллелограмма.

Урок 7: Признаки параллелограмма

На сегодняшнем уроке мы повторим основные свойства параллелограмма, а затем уделим внимание рассмотрению первых двух признаков параллелограмма и докажем их. В ходе доказательства вспомним применение признаков равенства треугольников, которые мы изучали в прошлом году и повторяли на первом уроке. В конце будет приведен пример на применение изученных признаков параллелограмма.

Пример на применение первого признака параллелограмма

Рассмотрим пример на применение признаков параллелограмма.

Пример 1. В выпуклом четырехугольнике 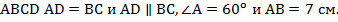Найти: а) углы четырехугольника; б) сторону .

Решение. Изобразим Рис. 4.

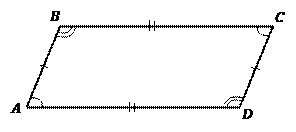
Рис. 4

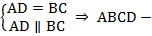параллелограмм по первому признаку параллелограмма.

А. 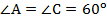по свойству параллелограмма о противоположных углах, 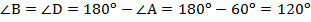по свойству параллелограмма о сумме углов, прилежащих к одной стороне.

Б. 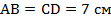по свойству равенства противоположных сторон.

Ответ. .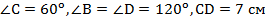

На следующем уроке мы рассмотрим еще один признак параллелограмма (третий).

Домашнее задание

1. Докажите, что если сумма углов, прилежащих к любой из сторон четырехугольника, равна 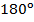, то этот четырехугольник – параллелограмм.

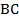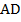2. Точки и – соответственно середины сторон и параллелограмма . Докажите, что четырехугольник 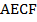– параллелограмм.

3. В треугольнике 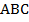медиана 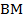перпендикулярна к стороне 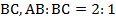. Найдите .

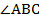Урок 8: Третий признак параллелограмма

Данный урок посвящён третьему признаку параллелограмма и его применению. На предыдущем уроке были изучены первый и второй признаки параллелограмма, которые основывались на свойствах сторон и углов параллелограмма. Третий признак основан на свойстве диагоналей параллелограмма. А именно, на том, что диагонали параллелограмма в точке пересечения делятся пополам. Признаки параллелограмма очень важны при решении целого ряда задач, поскольку позволяют доказывать то, что четырёхугольник является параллелограммом, а, значит, можно пользоваться его свойствами.

Пример задачи на третий признак параллелограмма и обобщение

Рассмотрим пример на применение третьего признака параллелограмма.

Пример 1

Дано:

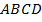–параллелограмм; 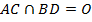. 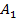– середина 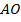, 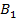– середина 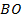, 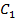– середина 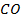, 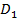– середина 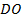(см. Рис. 2).

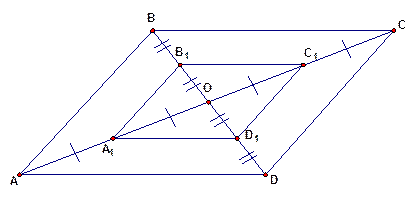
Рис. 2

Доказать: 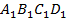– параллелограмм.

Доказательство:

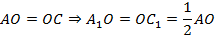
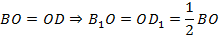
Значит, в четырёхугольнике 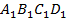диагонали в точке пересечения делятся пополам. По третьему признаку параллелограмма из этого следует, что 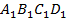– параллелограмм.

Доказано.

Если провести анализ третьего признака параллелограмма, то можно заметить, что этот признак соответствует свойству параллелограмма. То есть, то, что диагонали делятся пополам, является не просто свойством параллелограмма, а его отличительным, характеристическим свойством, по которому его можно выделить из множества четырёхугольников.

На следующем уроке мы рассмотрим решение различных задач про параллелограмм.

Домашнее задание

1. Диагонали четырёхугольника 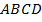пересекаются в точке 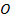. Является ли данный четырёхугольник параллелограммом, если 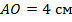, , 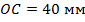, 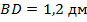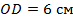. Ответ обоснуйте.

2. Диагонали четырёхугольника 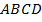пересекаются в точке 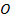. Известно, что 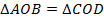. Докажите, что данный четырёхугольник – параллелограмм.

Урок 9: Задачи на параллелограмм.

На уроке мы, прежде всего, повторим уже изученные ранее свойства и признаки параллелограмма и все основные понятия, которые связаны с этой геометрической фигурой. Главной целью занятия будет рассмотрение нескольких примеров на применение знаний о параллелограмме. В процессе решения примеров познакомимся с важнейшей теоремой, связанной с параллельностью прямых, – теоремой Фалеса.

1. Повторение определения, свойств и признака параллелограмма

Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.

Определение. Параллелограмм– четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).

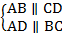
Рис. 1. Параллелограмм

Основные свойства параллелограмма:

Теорема.Первый признак параллелограмма.Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. 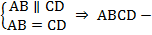параллелограмм.

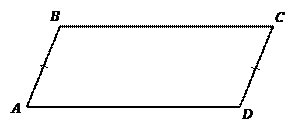
Рис. 2. Первый признак параллелограмма

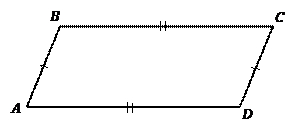
Рис. 3. Второй признак параллелограмма

Теорема. Второй признак параллелограмма.Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник –параллелограмм. 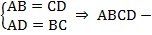параллелограмм.

Теорема. Третий признак параллелограмма.Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. 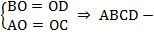параллелограмм.

Рис. 4. Третий признак параллелограмма

Задачи на параллелограммы

Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.

Пример 1. В параллелограмме проведены биссектрисы 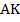и 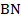, которые пересекаются в точке 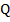. Найти .

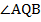Решение. Изобразим Рис. 5.

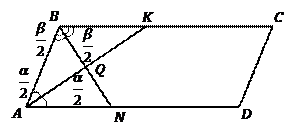
Рис. 5

Обозначим для удобства: 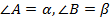. Следовательно, 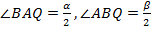поскольку 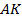и 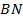биссектрисы.

По теореме о сумме внутренних углов треугольника .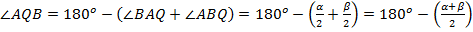

Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: 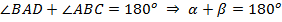. Тогда:

.

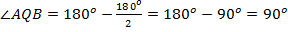Ответ. .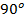

Пример 2. Прямая 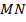, проведенная через середину 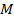стороны 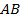параллельно стороне 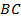треугольника 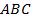пересекает третью его сторону в середине. Доказать, что 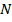– это середина .

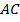Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .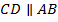

Рис. 6

Рассмотрим четырехугольник :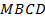

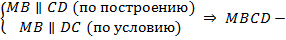параллелограмм по определению. Тогда по свойству равенства противоположных сторон 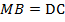, но по условию еще известно, что 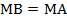, следовательно, .

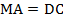Рассмотрим треугольник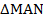и и :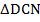

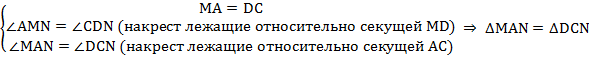по второму признаку равенства треугольников (по стороне и прилежащим углам).

Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что 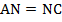. Это означает, что точка 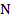является серединой стороны 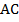. Что и требовалось доказать.

Доказано.

Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях.

Домашнее задание

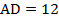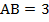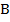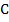1. В параллелограмме см, см, биссектрисы углов и пересекают сторону 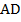в точках 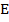и 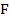. Найдите длину отрезка .

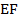2. Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен 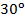. Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.

3. ^* Через середину 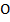диагонали 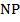параллелограмма 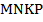проведена прямая, которая пересекает стороны 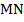и 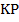в точках и соответственно. Докажите, что четырехугольник 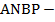параллелограмм.

Урок 10: Прямоугольник

На данном уроке мы будем рассматривать частный случай параллелограмма – прямоугольник. Мы введем его основные свойства, докажем теорему о равенстве диагоналей прямоугольника и сформулируем признак прямоугольника. Затем решим достаточно много задач, которые связаны с этой фигурой.

Признак прямоугольника

Теорема 2. Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Доказательство. Изобразим Рис. 3. Нам необходимо доказать, что изображенный параллелограмм с двумя равными диагоналями – прямоугольник, т.е. имеет прямой угол.

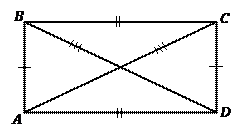
Рис. 3

Поскольку – параллелограмм, то можем воспользоваться его свойством: 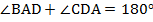. Кроме этого, 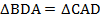– по трем сторонам ( 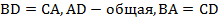), следовательно, 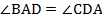. Тогда имеем:

прямоугольник, что и требовалось доказать.

Доказано.

Ромб и его свойства

Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма. Однако есть и специфические свойства, о которых пойдёт речь. Но для начала сформулируем одно из определений ромба.

Ромб –это параллелограмм, у которого все стороны равны.

Сформулируем и докажем теорему о свойствах ромба.

Теорема

Диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов) (см. Рис. 1).

Дано:

– ромб

Доказать:

.

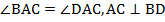Доказательс