Обобщающий комбинированный урок по проверке знаний
Нередко учитель использует в проверке знаний для учета успеваемости, так называемый балл, который составляется из совокупности всей работы ученика на уроке, в том числе и из ответа на проверочной беседе и при решении комбинированных задач. Это определенным образом повышает ответственность учащихся, дисциплинирует их. Проставление оценок за активное участие на таком уроке возможно при условии, что ответы учащегося последовательные, логические и дают достаточное основание для определенного вывода.
Пример 26. [36]
Математическая регата. (проверка знаний)
по теме «Признаки равенства треугольников».
1 (тур). Проверка знаний теории..
Указать верный ответ.
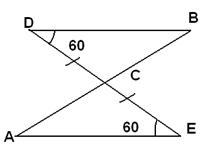Задача 1. Используя данные рисунки, найдите угол А, если < В = 800.
А. 60°;
В. 800;
С. другой ответ.
Каждому экипажу даются тесты с заданиями 1 тура. (За верный ответ – 1 бал).
По количеству набранных баллов 2 экипажа выходят во второй «заплыв» - тур, а проигравший экипаж отправляется в «утешительный» заплыв.
Тур). Решение задач.
Каждому экипажу даются задачи с выбором правильного ответа – задачи II тура. За каждый правильный ответ – 1 бал.
Задача 2. Найти смежные углы, если
известно, что один из них на40° больше
другого?
А. 70° и 110°;
В. 40° и 140°;
С. 70° и 210°.
Задания «дополнительного заплыва».
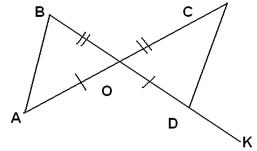
Задача 3. На рисунке ОВ = ОС, АО = ОD, < ВАО = 700. Чему равен угол СDК?
А. 110°; В. 70°; С. Не знаю.
Задача 4. Один из углов равнобедренного треугольника равен80°. Найти остальные углы.
А. Задача имеет 1 решение: 80°; 50°; 50°.
В. Задача имеет 2 решения: 80°; 50°; 50° и 80°; 80°; 20°.
С. Для решения задачи не хватает данных.
Устные задачи:
1 В равнобедренном треугольнике одна сторона равна 3 см, другая – 8 см. Чему может быть равна третья сторона?
2. Как можно назвать равнобедренный треугольник, у которого основание равно боковой стороне?
3.Всякий ли равносторонний треугольник является равнобедренным?
4. Периметр равностороннего треугольника равен 6 см. Чему равна длина каждой его стороне?
Количество дополнительных задач зависит от времени урока, можно ограничиться одной задачей (т.е. до победы одного из экипажей).
«Центр управления» регатой подводит итоги, а в это время экипажи получают «задание» (домашнее задание).
ЗАКЛЮЧЕНИЕ
Геометрия в целом, как и ее основные составляющие- фигуры, логика и практическая применимость – позволяют учителю гармонично развивать образное и логическое мышление ребенка любого возраста, прививать ему навыки практической деятельности.
Логическое мышление- это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь ее извлечь. Очень часто учащимся при изучении геометрии приходится путем рассуждений выводить разнообразные формулы, правила, доказывать теоремы. А это значит, что для успешного обучения геометрии надо настойчиво учить детей правильно рассуждать. Решение всякой геометрической задачи - это цепь рассуждений.
Однако, в настоящее время в современных школах учителя все меньше внимания уделяют развитию логического мышления учащихся. Процесс обучения нередко сводится к механическому заучиванию материала. Для учителя главное, как хорошо ученик знает теорию, но это еще, не значит сможет ли он применить ее на практике. Поэтому большая роль в развитии логического мышления учащихся принадлежит учителю, от того, как он преподносит учебный материал, требует ли от учеников логических рассуждений. Известно, что доказательство теорем и решение задач на доказательство являются одними из основных путей развития логического мышления учащихся. Поэтому при обучении учащихся доказательству следует требовать от них четких логических посылок, предоставлять больше самостоятельности при решении задач на доказательство.
Таким образом, чтобы создать опору для успешного обучения, необходимо обратить внимание на пути развития логического мышления средствами обучения доказательствам на уроках геометрии. Процесс обучения доказательству неразрывно связан с логическим мышлением, и учителю важно об этом помнить.
БИБЛИОГРАФИЯ.
1. Барыкин К.С. Сборник геометрических задач на доказательство. М., 1954-151с.
2. Березина Л.Ю. Геометрия в 7-9 классах. М., 1990-334с.
3. Болтянский В.Г. Как устроена теорема? //Математика в школе 1973-№1.
4. Брадис В.М. Ошибки в математических рассуждениях. М., 1959-176с.
5. Вопросы развития логического мышления в процессе школьного обучения //Тамбовская правда, 1959-66с.
6. Геометрия: теория и ее использование для решения задач /Яковлев Г.Н. М., 1973-184с.
7. Груденов Я.И. Изучение определений, аксиом, теорем. М., 1981-95с.
8. Далингер В.А. Обучение учащихся доказательству теорем. Омск, 1990.
9. Дубнов Я.С. Ошибки в геометрических доказательствах. М., 1969-69с.
10. Журавлев Г.Е. Системные проблемы развития математической психологии. М., 1983-204с.
11. Зыкова В.И. Формирование практических умений на уроках геометрии. М.,1963-200с.
12. Медяник А.И. Учителю о школьном курсе геометрии. М., 1984-95с.
13. Мищенко Т.М. , Райляну А.И. Из опыта работы учителей Молдовы. // Математика в школе 1991-№1.
14. Мостовой А.И. Различные способы доказательств в курсе геометрии восьмилетней школы. М., 1965-102с.
15. Преподавание алгебры и геометрии в школе / сост. О.А.Боковнев М., 1982-123с.
16. Преподавание геометрии в 6-8 классах / В.А.Гусев. М., 1979-287с.
17. Подходова Н.С. К проблеме личностно-ориентированного обучения геометрии. // Математика в школе. 2000-№10
18. Притуло Ф.Ф. Методика изложения геометрических доказательств. М., 1958-108с.
19. Развитие логико-вероятностные мышления в школе. // Математика в школе 1994-№18.
20. Волович М.Б. «Ключ к пониманию геометрии» Издательство «Аквариум» 2006г.
21. Сборник статей по вопросам преподавания геометрии в средней школе. / Стратилатова П.В. М., 1958-191с.
22. Итоговые тесты по геометрии (9 класс) Федеральный Центр тестирования , 2005г.
23. Терешин Н.К. Еще раз о доказательстве//Математика, 2002-№35.
24. Тимощук М.Е. Построение доказательств по геометрии. Омск, 1999-51
25. Финкельштейн В. Н. Первые теоремы//Математика, 2002-№35
26. Перед встречей с доказательством//Математика ,2007-№9 с.41
27. Чичигин В.Г. Методика преподавания геометрии. М., 1959-392с.
28. Признаки равенства треугольников по учебнику Л.С.Атоносяна // Математика, 2007-№10 с.12.
29. Геометрия 9кл «Тематические тесты» Федеральный Центр тестирования, 2008г.
30. Русских Г.А. Развитие учебно-исследовательской деятельности
учащихся// Дополнительное образование.2001. № 7-8.
31. Савенков А.И. Одаренный ребенок в массовой школе/ Библиотека журнала «Директор школы» – М.: Сентябрь, 2001
32. Счастная Т.П. Рекомендации по написанию научно исследовательских работ// Исследовательская работа школьников. 2003. № 4.
33. И.В. Усачева, И.И. Ильясов. Формирование учебной исследовательской деятельности. – М., 1986.
34. Репетитор по геометрии. 10, 11 класс. – М.: ООО «Акелла», 2008.
35. Репетитор по геометрии. – М.: ООО «Акелла», 2008.
36. Геометрия. 7-9 класс. – М.: ООО «Новая школа», 2007.
37. Геометрия. 10-11 класс. – М.: ООО «Новая школа», 2007.
38. Репетитор по геометрии. 10, 11 класс. – М.: ООО «Акелла», 2008.
39. Репетитор по геометрии. – М.: ООО «Акелла», 2008.
40. Геометрия. 7-9 класс. – М.: ООО «Новая школа», 2007.
41. Геометрия. 10-11 класс. – М.: ООО «Новая школа», 2007.