Необходимые условия понимания и умения делать логические выводы.

Обучение умению выводить логические следствия из имеющихся предпосылок – одна из главных задач учителя на уроках геометрии. Элементарные навыки поиска приобретаются при решении задач. При этом объяснение учителя не должно быть воспроизведением текста учебника, иначе для многих учащихся доказательство остается непонятным и тогда, весь процесс его усвоения сводится к заучиванию без понимания смысла. От чего же зависит возможность понимания доказательства?

Прежде всего, должно быть обеспечено яркое и отчетливое понимание доказываемого тезиса и владение аргументами. Это необходимые предпосылки доказательства. В самом же процессе доказательства возникают еще 2 проблемы:

1. понимание строения и правильности каждого умозаключения в отдельности;

2. понимание последовательности связи умозаключений.

Пример 20.

При отработке понятий медианы, высоты, биссектрисы треугольника необходимо уделять внимание не запоминанию формулировок, а их пониманию, вытекающих следствий из них и умозаключений с помощью таких упражнений: Если в условии сказано: « Проведена медиана ВК в треугольнике АВС» из этого следует………………… Если в условии сказано: « проведена высота ВК в треугольнике АВС» из этого следует………………… Если в условии сказано: « Проведена биссектриса ВК в треугольнике АВС» из этого следует…………………

При доказательстве теоремы о свойстве биссектрисы равнобедренного треугольника необходимо , чтобы учащиеся видели :

а) два равных треугольника - равенство соответствующих сторон;

б) определение медианы – значит, биссектриса является медианой;

в) два равных треугольника - равенство соответствующих углов;

г) определение высоты, свойство смежных углов – биссектриса является высотой.

В процессе отыскания доказательства не следует задавать учащимся много вопросов, тем более по пройденному материалу ,так как это отвлекает учащихся и мешает им сосредоточится на главном. Если класс достаточно подготовлен и отыскание доказательства уже вошло в систему, то число вопросов, задаваемых классу, может быть уменьшено, - нужно оставить только те вопросы, которые непосредственно связаны с открытием нового; такие, где учащимся нужно подумать, сообразить, а не просто вспомнить, отыскание доказательства еще и потому, что теперь возникает возможность привлечь учащихся к активному участию в изложении найденного доказательства. Самому приему отыскания доказательства можно и нужно придавать различные формы в зависимости от трудности доказательства, возраста и подготовки учащихся. К отысканию доказательства во всех случаях должны привлекаться учащиеся. Активность учащихся должна проявляться в открытии нового : в умении сделать выводы; в попытках продолжить ход рассуждений. Рассуждение, рассказ и вопросы учителя должны возбудить активное мышление учащихся, подготовить их к самостоятельному выводу, возбудить потребность высказывать этот вывод или привести свои предположения о том, как следовало бы поступить дальше.

Пример 21.

Доказательство теоремы о свойстве биссектрисы равнобедренного треугольника простое, поэтому можно предложить учащимся самостоятельно провести исследование и доказать, что она является и медианой и биссектрисой.

Выделить посылки:

а) признаки равенства треугольников;

б) определение медианы;

в) определение биссектрисы:

г) определение высоты:

д) свойство смежных углов.

Доказательство провести по готовому чертежу:

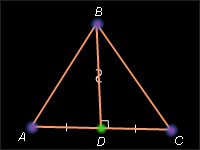
Упражнения в оформлении доказательств помогают лучшему усвоению и более прочному запоминанию самих доказательств, вводит учащихся в круг требований, предъявляемых к доказательству, и вырабатывают умение изложить его самостоятельно; они способствуют развитию речи и мысли; воспитывают умение придать им точную и законченную форму, помогают направить их в русло полной работы.

Пример 22.

По готовому чертежу учащиеся делают записи самостоятельно:

Дано: : АВС -равнобедренный

АС – основание АВС

АD - биссектриса АВС

Доказать: АD – медиана, высота.

Доказательство: Большое влияние на результат исследований оказывает форма изложения рассуждений. Чтобы сделать эту форму более доступной и легче усвояемой необходимо следующее:

1. Ввести в изложение краткие разъяснения метода основной идеи плана доказательства и целесообразности дополнительных построений

2. Выделять в нем узловые моменты.

Пример 23.

Урок по теме «Соотношения между сторонами и углами треугольника»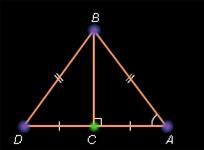

Подготовка к уроку:

Задача: В равнобедренном треугольнике (АВ=АС) величина угла В равна 55 градусов. Найти величину угла А.

В случае затруднения при решении этой задачи последовательно использовать следующие вопросы – подсказки. Совсем не обязательно предлагать полный перечень подсказок. Его следует прервать сразу, как только ученик «увидит» решение.

а) перечисли все стороны треугольника;

б) назови равные стороны;

в) к какому виду принадлежит треугольник;

г) какие свойства равнобедренно треугольника могли бы помочь решить задачу;

д) какую сторону можно назвать основанием;

е) если треугольник равнобедренный , то что можно сказать про его углы при основании; и т.д.

Итак, успех в доказательстве логических следствий определяется не применением какого-нибудь метода или приема, а системой преподавания в целом. И весь комплекс необходимых условий понимания и умения делать логические выводы заключаются в следующем:

1. Ученик должен иметь ясное представление о сущности доказательства, его строении, его видах и требованиях, к нему предъявляемых.

2. Необходимо вести планомерную и систематическую работу по воспитанию у учащихся потребности в доказательстве.

3. Существенно важно, чтобы учитель и учащиеся понимали цели доказательства логических следствий.

4. Учитель должен раскрыть перед учеником всевозможные варианты исследований и умения делать аргументированные выводы из имеющихся предпосылок.

Для решения этой задачи учитель должен:

А) Неустанно заботиться о развитии логического мышления и речи учащихся;

Б) Добиваться предельно ясного понимания формулировки основных посылок, теорем и следствий.

В) Уделять самое серьезное внимание процессу доказательств и логических исследований.

Изучив литературу по данному вопросу, считаю, что выводы следствий играют важную роль при формировании логического мышления школьников. Необходимо ставить перед детьми основные цели исследований и доказательств, вести подготовительную работу, четко формулировать условие и заключение утверждений (теорем, следствий, задач). Показать детям, что процесс доказательства заключается в цепочке умозаключений, не зависимо оттого, каким методом оно ведется.

Диагностический модуль.

Для обучения большое значение имеет установление уровня обученности школьников – уровня определенных стандартов необходимых знаний. Для того чтобы была непрерывная система образования, нужно проверять и оценивать знания и умения своих учеников по всем пройденным темам и разделам. Опрашивать их по изученному материалу, проводить письменные проверочные работы, диктанты, тестирования, а также и зачетные уроки. Далее оценивать результаты проверки в баллах или оценочных суждениях. Учителю контроль знаний позволяет определить уровень усвоения учебного материала по математике и в случае необходимости провести их коррекцию. Ученику – привести в систему усвоенной за определенное время учебный материал, обобщить его, выделить главное, акцентировать на нем внимание, скорректировать в случае необходимости отдельные знания и в оценке и отметке увидеть результаты своей деятельности. Диагностировать, контролировать, проверять и оценивать знания и умения учащихся по математике нужно последовательно, согласно порядку изучения математического материала. Умелое владение учителем различными формами контроля знаний способствует повышению заинтересованности учащихся в изучении предмета, обеспечивает активность учащихся на занятиях. При этом контроль не должен быть односторонним – проверять следует как сами знания, так и умения их применять. Лучших результатов достигаются те учителя, которые ориентируются в первую очередь на проверку уровня развития учащихся, а не на проверку их памяти.

Проблемой необходимости проверки знаний, умений и навыков учащихся по математике занимаются многие педагоги и научные работники в области дидактики: Ю.Я. Яковлев, В.А.Оганесян, Ю.М.Колягин, А.В.Соколова, В.В.Пикан и другие [2]. Публикации, посвященные вопросу использования различных форм контроля можно найти в газетах «Математика» и в журнале «Математика в школе». Главное в проверке знаний не столько то, чтобы проверить объем и качество усвоения материала, сколько в том, чтобы быть в курсе того, как развивается мышление ученика. Как протекает этот мыслительный процесс - легко или трудно, прямым или окольным путем человек идет к цели; формально или осмысленно применяет соответствующие теоремы, аксиомы, следствия; использует исследовательский метод рассуждений, умеет делать логические выводы из имеющихся посылок. Все это при чисто практическом способе проверки знаний большей частью остается скрытым от контроля учителя.

Устная проверочная работа.

Наиболее хорошим методом проверки знания фактического материала и качества мышления школьника является устный опрос. При проведении устного опроса учитель стремится проверить, насколько учащиеся овладели учебным материалом, и, кроме того, вовлечь, по возможности всех учащихся в активную работу. Все это можно выяснить, слушая ответ ученика .

Важное значение имеет устный опрос для развития математической речи учащихся: ведь это чуть ли не единственный вид речевой практики ученика на уроке. Для решения этой задачи большое значение имеет характер заданий и вопросов учителя. Следует чаще предлагать вопросы, требующие объяснения: объясни, как ты решил эту задачу, какие теоремы, следствия применил для обоснования вывода. Полезно включать задания на сравнение: сравни эти треугольники и т. д. При устном опросе дети высказывают свою мысль. Нужно учить высказываться, грамотно оформлять свою мысль. При рецензии ответа используется схема:

-все ли существенное освещено в рассуждениях;

-сумел ли ученик добавить что-либо к учебнику;

-насколько последовательно изложил доказательство;

-аргументированы ли умозаключения;

-правильно ли сделан вывод;

-оценить речь учащегося.

Ученики к ответу должны готовиться по схеме (по плану):

-главная мысль;

-аргументы для ее развития;

-вывод.

Устный опрос позволяет обстоятельно выяснить знания учащиеся, однако он требует много времени, что ограничивает возможность проверить большое количество учащихся. Кроме того, в устном опросе вопросы учителя и ответы учащихся нигде не фиксируются. Это мешает учителя возможности сравнивать ответы разных учащихся на один и тот же вопрос, ответы оного и того же ученика, данные в разное время учебного года. Но, несмотря на эти недостатки, устный опрос - исключительно ценный элемент урока, если его структура проработана в деталях. Проводя любой вид опроса учитель обязан создать такую психологическую обстановку опроса, при которой отвечающий ученик чувствовал бы себя совершенно спокойно, непринужденно, бодро, чтобы его ничто не нервировало, не подавляло, не мешало. Только при этом условии возможно объективное, полное и глубокое выявление истинных знаний учащегося и, справедливая оценка, которую он должен получить.

Фронтальный опрос – это, в сущности проверочная беседа учителя с классом. Учитель задает классу вопросы, отдельные учащиеся коротко отвечают на них. Обычно прибегают к проверочной беседе тогда, когда не предполагается специально оценить знания учащихся, но необходимо восстановить в их памяти те или иные явления, закономерности, определения. Нередко учителя и эту форму проверки знаний используют для учета успеваемости, так называемый балл составляется из совокупности всей работы ученика на уроке, в том числе и из ответа на проверочной беседе. Это определенным образом повышает ответственность учащихся, дисциплинирует их. Проставление оценок за активное участие в проверочной беседе возможно при условии, что ответы учащегося дают достаточное основание для определенного вывода. Подготавливая проверочную беседу с классом, надо совершенно отчетливо представлять себе, с какой конкретной целью она предпринимается. В главном назначении проверочной беседы является подведение прочного фундамента под усвоение материала, который предстоит изучать учащимся. Поэтому ее обычно и проводят перед изучением нового материала.