Учебный модуль темы «Треугольник» в средней школе

Государственный стандарт образования по геометрии требует такой уровень подготовки учащихся при котором учащиеся должны : дать определение фигуры, сформулировать ее свойство или признак, указанный в теореме, и доказать эту теорему выстраивать логические предложения при решении задач уровня базовой и профильной подготовки

При этом учащиеся должны:

• дать определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж;

• правильно воспроизвести формулировку теоремы, проиллюстрировав ее выполнением чертежа по условию теоремы;

• привести доказательство теоремы, при этом доказательство считается выполненным верно, если учащийся правильно привел схему доказательства, обосновал все логические шаги, выполнил чертежи, которые правильно отражают, кроме условия, еще и ход доказательства отражающий ее содержание и смысл.

Кроме того, учащиеся должны показать умение геометрически грамотно выполнять чертежи: правильно отмечать равные элементы фигур, проводить медианы треугольников, высоты треугольников, проекции и т.д.

При этом ученик должен владеть методами доказательств, интегрировать знания из различных тем курса планиметрии и стереометрии, владеть исследовательскими навыками, а также уметь найти и применить нестандартные приемы рассуждений.

Здесь требуются:

· умение применять известные факты в измененной ситуации;

· знания о свойствах различных конфигураций;

· умение проводить логические исследования;

· владение способами и методами решения различных типов задач.

Именно такие требования в последние годы предъявляются математическим сообществом к умению решать геометрические задачи. Этот подход реализуется и при отборе задач в варианты ЕГЭ по математике

Изучение темы «Треугольник» в курсе планиметрии предполагает раскрытие следующих тем [27]:

1. Внутренние и внешние углы треугольника. Стороны треугольника, его медианы, биссектрисы, высоты.

2. Остроугольный, прямоугольный и тупоугольный треугольники.

3. Равнобедренный треугольник. Свойства и признаки. Равносторонний треугольник.

4. Признаки равенства треугольников.

5. Неравенство треугольника. Перпендикуляр и наклонная.

6. Сумма углов треугольника. Сумма углов выпуклого многоугольника.

7. Теорема Фалеса. Средняя линия треугольника.

8. Подобие треугольников. Признаки подобия треугольников.

9. Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора.

10. Синус, косинус, тангенс и котангенс угла от 0° до 180°.

11. Теорема синусов и теорема косинусов. Решение треугольников.

12. Замечательные точки треугольника – точки пересечения: серединных перпендикуляров (центр окружности, описанной около треугольника), биссектрис (центр окружности, вписанной в треугольник), медиан, высот.

Тема «Треугольник « применяется при изучение свойств геометрических тел в стереометрии, что способствуют развитию пространственных представлений учащихся, освоение способов вычисления практически важных геометрических величин и дальнейшее развитие логического мышления учащихся в старших классах при изучении таких тем, как:

1. Параллелепипед и пирамида

2. Свойства граней и диагоналей параллелепипеда

3. Свойства параллельных сечений в пирамиде

4. Боковая поверхность призмы и пирамиды

Упражнения.

Этому курсу присущ систематизирующий и обобщающий характер изложений, направленность на закрепление и развитие умений и навыков, полученных в основной школе. Высокий уровень абстрактности изучаемого материала, логическая строгость систематического изложения соединяется с привлечением наглядности на всех этапах учебного процесса и постоянным обращением к опыту учащихся. Умение изображать важнейшие геометрические тела, вычислять их объёмы и площади поверхностей имеют большую практическую значимость. Для эффективной реализации курса необходимо использовать разнообразные формы, методы и приёмы обучения, делая особый упор на развитие самостоятельности, познавательного интереса и творческой активности учащихся. Для этой цели проводят уроки:

1. лекции;

2. уроки консультации;

3. самостоятельные работы;

4. зачеты;

5. итоговые контрольные работы.

Для тех учащихся, которые хотят продолжить образование, связанное с геометрией, практикум решения задач исследовательским методом будет способствовать успешной сдаче единого государственного экзамена по математике, вступительного экзамена в ВУЗ и успешного обучения в ВУЗ-е

Решение стереометрических задач на свойства геометрических тел, нахождение площадей поверхностей и объемов этих тел, позволяют получить углубленные знания по геометрии и дают ориентацию на инженерные профессии, связанные с математикой.

Пример:

Задача 1. В правильной четырехугольной пирамиде боковое ребро наклонено к плоскости основания под углом 45°. Найдите плоский угол при вершине.

Исследование при решении этой задачи можно провести без чертежа:

Первый способ:

Пусть боковое ребро равно a. Оно наклонено к основанию под углом 45°, поэтому проекция этого ребра равна половине диагонали основания, то есть 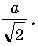Вторая половина диагонали образует с ней прямой угол и дает прямоугольный равнобедренный треугольник, гипотенуза которого равна a, следовательно, боковая грань – равносторонний треугольник с углом при вершине 60°

Второй способ:

Теорема. Если некоторая прямая образует с прямой на плоскости угол , с проекцией на эту плоскость ,
а проекция с прямой на плоскости угол , то

cos  = cos  cos .

Применительно к данной задаче это выглядит так.

Обозначим через  угол между боковым ребром и ребром основания, между боковым ребром и проекцией – через  ( = 45°), между проекцией и ребром основания – через  ( = 45°). Тогда по теореме трех косинусов имеем 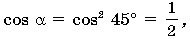следовательно,  = 60°.

Так как боковая грань – равнобедренный треугольник, то в данном случае он и равносторонний. Плоский угол при вершине равен 60°.

Иначе задачу можно сформулировать так: плоский угол при вершине равен 60°. Найдите угол наклона бокового ребра к основанию.

Задача2.

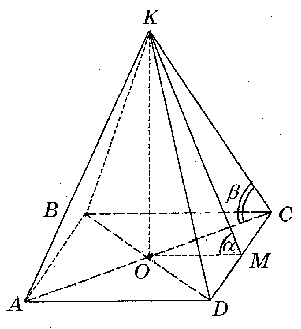В правильной четырехугольной пирамиде площадь боковой поверхности в n раз больше площади основания. Определите угол наклона бокового ребра к основанию.

Решение. Обозначим угол KCO через – , линейный угол двугранного угла CD – угол KMO – через .

Учащиеся знают, что если некая фигура образует с плоскостью угол , а проекция этой фигуры на плоскость имеет площадь S_о, то площадь фигуры 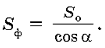Следствием из этой теоремы является зависимость между площадями основания правильной пирамиды и боковой поверхности. В рассматриваемом случае имеем

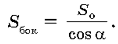
Так как площадь боковой поверхности в n раз больше площади основания, то имеем 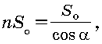откуда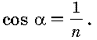

Решение задачи сводится к определению угла , если известен угол .

Углы  и  принадлежат двум прямоугольным треугольникам, «связанным» общим катетом KO. Вторые катеты OC и OM легко вычисляются один через другой (гипотенуза и катет прямоугольного равнобедренного треугольника). Поэтому используем функцию тангенс. Имеем

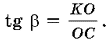
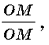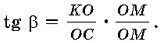Используем следующую «изюминку»: умножим эту дробь на дробь имеем Перепишем иначе это выражение: 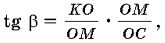имеем 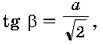где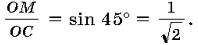

Задача свелась к определению tg , если известен его косинус. Как же это сделать?

Учащиеся знают формулу

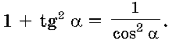
Но ученик может «случайно» забыть формулу или ошибиться в 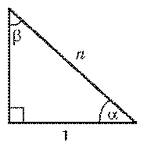преобразованиях. Я же в свое время заставлял учеников ни в коем случае не решать по формулам, а находить значение любой тригонометрической функции через известную формулу только устно.

Представим в уме прямоугольный треугольник. Обозначим один из острых углов через a, гипотенузу – через n, прилежащий к углу a катет положим равным 1. Второй катет по теореме Пифагора равен 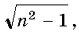тогда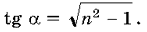

Задача решена. Имеем

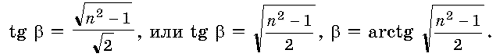
Без использования этих двух «изюминок» решение задачи было бы сложнее. Для самоконтроля можно решить следующую задачу.

В правильной шести- или n-угольной пирамиде высота образует с боковым ребром угол a. Определите, какой угол образует высота с боковой гранью.