Прямая линия, принадлежащая плоскости
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.6.2).
Задача. Дана плоскость (n,k) и одна проекция прямой m2. Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k. Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k. Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.
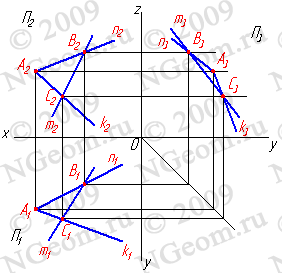
Рисунок 6.2 Прямая и плоскость имеют две общие точки
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.6.3).
Задача. Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k. Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1. Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.
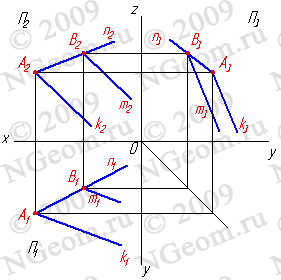
Рисунок 6.3 Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости
Главные линии в плоскости
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).
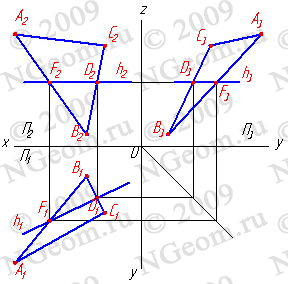
Рисунок 6.4 Горизонталь
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).
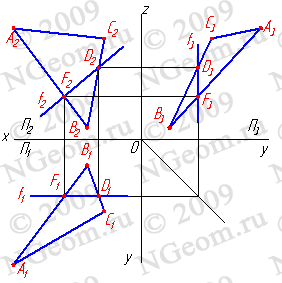
Рисунок 6.5 Фронталь
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
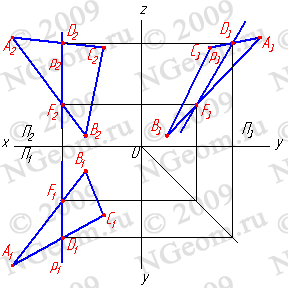
Рисунок 6.6 Профильная прямая
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.
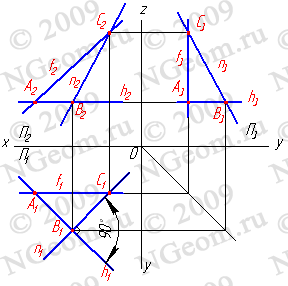
Рисунок 6.7 Линия наибольшего ската
18. Перпендикулярность прямой к плоскости. Определение расстояния от точки до плоскости.
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Две плоскости, перпендикулярные одной прямой, параллельны между собой.
| Если из одной точки вне плоскости проведены к ней перпендикуляр и наклонные, то длина перпендикуляра меньше длины любой наклонной; наклонные с равными проекциями равны; из двух наклонных большую длину имеет та, у которой больше проекция. О трех перпендикулярах. Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость. |
19. Способы преобразования проекций.
Четыре основные задачи, решаемые методами преобразования
1. Прямую общего положения преобразовать в прямую уровня.
2. Прямую общего положения преобразовать в проецирующую прямую.
3. Плоскость общего положения преобразовать в проецирующую плоскость.
4. Плоскость общего положения преобразовать в плоскость уровня.
Достигается это:
а) введением дополнительных плоскостей проекций так, чтобы прямая линия или плоская фигура, не меняя своего положения в пространстве, оказалась в частном положении в новой системе плоскостей проекций (способ перемены плоскостей проекций);
б) изменением положения прямой линии или какой-либо фигуры путем поворота вокруг некоторой оси так, чтобы прямая или фигура оказалась в частном положении относительно неизменной системы плоскостей проекций (способ вращения и плоскопараллельного перемещения).
2. Замена плоскостей проекций
Сущность способа замены плоскостей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций (рис. 75).
При переходе к новой системе одну из плоскостей проекций заменяют новой таким образом, чтобы данный геометрический элемент (прямая, плоскость) занял частное положение и проецировался без искажения. При решении ряда задач, например, требуется преобразовать прямую общего положения в прямую уровня, а затем -- в проецирующую, выполнив при этом последовательно два преобразования.
Рассмотрим ход решения задач.
РЕШЕНИЕ I ОСНОВНОЙ ЗАДАЧИ. Для того, чтобы прямая АВ стала линией уровня (рис. 76, а), следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось x1 будет параллельна одной из проекций прямой. Проведем ось параллельно горизонтальной проекции АВ. Новая плоскость проекций V1 расположится параллельнопрямой АВ, которая проецируется на эту плоскость в истинную величину Новая ось x1 и плоскость проекции V1 могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.
