Предмет начертательной геометрии.

Предмет начертательной геометрии.

Начертательная геометрия теория изображения пространственных тел. Цель: изучение правил и способов для решения инженерных задач: создание новых чертежей и чтение уже созданных.

Разум человека уже владеет 3мя ключами открывающими всё: цифрой, буквой, нотой. Геометрия добавляет еще один ключ- линию.

Линия- язык графики, наиболее естественный язык для передачи информации. НГ- грамматика этого языка.

Методы проецирования. Основные св-ва.

в основе НГ лежит метод проекции. Проекция геом. тела называется изображение его на плоскости, или на поверхности расположенной вне этого тела.

Чтобы осуществить процесс проекции нужно знать:

а)что проецировать(объект проекции).

б)на что проецировать(поверхн.пр).

в)как проецировать(способ пр).

а)Любые объекты.

б) в кач-ве поверхности проец. может быть использована любая поверхность – плоская(лист

бумаги), сферическая(купол планет), цилиндрическая(экран круговой панорамы.

в) Существуют два способа проецирования: центральное и параллельное.

Параллельное делится на 2-е разновидности: косоугольная, прямоугольная.

Частный случай- центральное проецирование с несобственным центром, то есть отнесённом в бесконечность. Проецирующие лучи превращаем в || прямые. проец. лучи могут быть расположены к α под острым или прямым углом.

(косоугольным) (прямоугольным)

Центральное(коническое) пусть в простр. имеется (.) и пл(α). точка не лежит в этой плоскости. Центра проецирования в (.)S- центр проекции. Посылаем луч из (.)S через (.) А до пересечения с (α)- получаю её проекцию.

Координатный метод: комплексный чертёж Монжа.

Эпюр — (от франц. epure — чертеж), чертеж, на котором пространственная фигура изображена методом нескольких (по ГОСТу 3, но не всегда) плоскостей. Обычно оно даёт 3 вида: фронтальную, горизонтальную и профильную проекции. Чертеж проецируется на взаимно перпендикулярные, а затем развернутые плоскости.

Точка общего и частного положения на эпюре Монжа.

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.
Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей

Прямые общего и частного положения на эпюре Монжа.

Прямая линия в пространстве может занимать разные положения.

Произвольное расположение под произвольным углом (не 90⁰,|\|), занимать частные положения || или _|_ плоскостям проекции. Прямая может быть задана двумя(.), для её построения достаточно иметь проекции 2-х (.). Прямая наклонённая под некоторым углом не равным 90⁰ ко всем плоскостям проекции (п1,п2,п3) называется прямой общего положения.

Прямые частного положения.

1)Прямые уровня- || п1,п2,п3.

а)горизонталь h||п1

б)фронталь f||п2

в)профильная прямая П||п3

2) Прямые проецирования ( проецирующие прямые) ( на одной пло пр в (.))

_|_п1,п2,п3

а)горизонтально проецирующая _|_п1

б)фронтально проецирующая _|_п2

в) профильная проецирующая _|_п3

Относительное положение двух прямых:

Прямые в пространстве могут занимать разные положения: быть ||. пересекающимися и скрещивающимися.

Параллельные прямые.

Проекции 2-х || прямых параллельны между собой => если прямые в пространстве ||, то их проекции ||.

Пересекающиеся прямые.

прямые линии имеющие общую (.) назыв пересекающимися. Если прямые линии пересекаются, то их одноимённая проекция пересекаются между собой в (.) которая является проекцией точки пересечения этих прямых.

Скрещивающиеся прямые.

Прямые не пересекающиеся и не параллельные, являются скрещивающимися. Скрещ. прямые не имеют общих точек. Если их одноим проекц пересек, то (.) пересеч не могут лежать на одной линии связи.

Теорема о проецировании прямого угла(расст от (.) до прям уровня).

Свойство проецирующих плоскостей.

Свойство проецирующих плоскостей собирать одноименные проекции всех элементов, расположенных в данной плоскости.

Свойства и признаки

Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну

Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны

Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях

Главные линии в плоскости

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h//П1)(рис.6.4).

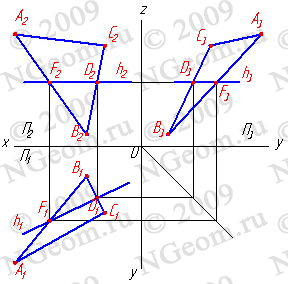
Рисунок 6.4 Горизонталь

2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (f//П2)(рис.6.5).

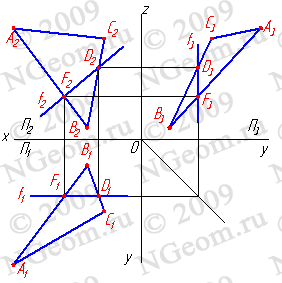
Рисунок 6.5 Фронталь

3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (р//П3) (рис.6.6). Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

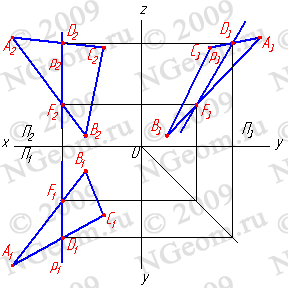
Рисунок 6.6 Профильная прямая

4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.6.7). Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

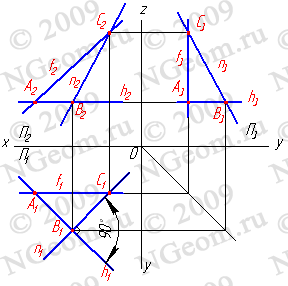
Рисунок 6.7 Линия наибольшего ската

18. Перпендикулярность прямой к плоскости. Определение расстояния от точки до плоскости.

Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.

Признак перпендикулярности прямой и плоскости.

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.

Две прямые, перпендикулярные одной плоскости, параллельны между собой.

Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.

Две плоскости, перпендикулярные одной прямой, параллельны между собой.

Если из одной точки вне плоскости проведены к ней перпендикуляр и наклонные, то длина перпендикуляра меньше длины любой наклонной; наклонные с равными проекциями равны; из двух наклонных большую длину имеет та, у которой больше проекция. О трех перпендикулярах. Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость.

19. Способы преобразования проекций.

Четыре основные задачи, решаемые методами преобразования

1. Прямую общего положения преобразовать в прямую уровня.

2. Прямую общего положения преобразовать в проецирующую прямую.

3. Плоскость общего положения преобразовать в проецирующую плоскость.

4. Плоскость общего положения преобразовать в плоскость уровня.

Достигается это:

а) введением дополнительных плоскостей проекций так, чтобы прямая линия или плоская фигура, не меняя своего положения в пространстве, оказалась в частном положении в новой системе плоскостей проекций (способ перемены плоскостей проекций);

б) изменением положения прямой линии или какой-либо фигуры путем поворота вокруг некоторой оси так, чтобы прямая или фигура оказалась в частном положении относительно неизменной системы плоскостей проекций (способ вращения и плоскопараллельного перемещения).

2. Замена плоскостей проекций

Сущность способа замены плоскостей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций (рис. 75).

При переходе к новой системе одну из плоскостей проекций заменяют новой таким образом, чтобы данный геометрический элемент (прямая, плоскость) занял частное положение и проецировался без искажения. При решении ряда задач, например, требуется преобразовать прямую общего положения в прямую уровня, а затем -- в проецирующую, выполнив при этом последовательно два преобразования.

Рассмотрим ход решения задач.

РЕШЕНИЕ I ОСНОВНОЙ ЗАДАЧИ. Для того, чтобы прямая АВ стала линией уровня (рис. 76, а), следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось x₁ будет параллельна одной из проекций прямой. Проведем ось параллельно горизонтальной проекции АВ. Новая плоскость проекций V₁ расположится параллельнопрямой АВ, которая проецируется на эту плоскость в истинную величину Новая ось x₁ и плоскость проекции V₁ могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.

Классификация поверхностей. Образование поверхностей.

Построение развёрток.

1. Построение разверток поверхностей. Общие указания

При изготовлении различных конструкций и изделий из листового материала имеет большое значение построение разверток поверхностей. Если представить себе поверхность как гибкую нерастяжимую пленку, то некоторые из них путем изгиба можно совместить с плоскостью без разрывов и деформаций. Такие поверхности относятся к развертывающимся, а полученную в результате развертывания поверхности плоскую фигуру называют разверткой этой фигуры.

Разверткой поверхности тела называется фигура, полученная путем совмещения его поверхности с плоскостью.

Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью всех его граней.

Поверхность и ее развертку можно рассматривать как две геометрические фигуры, между точками которых установлено взаимно однозначное соответствие. При развертывании (и свертывании) поверхности непрерывность поверхности не нарушается, не изменяется расстояние между точками поверхности и соответственно длина отрезков линий, углы между пересекающимися линиями в точках их пересечения и величины площадей фигур на поверхностях.

Те поверхности, которые нельзя совместить без разрывов и деформаций, относятся к неразвертываемым.

В практике возникает необходимость изготовления из листового железа не только развертывающихся плоскостей. Теоретически точно развертываются только гранные поверхности, торсы, конические или цилиндрические поверхности. При развертывании конических и цилиндрических поверхностей общего вида в практике их аппроксимируют вписанными гранными поверхностями. В этом случае, чем больше граней содержит вписанная поверхность, тем точнее ее развертка. Построенные таким образом развертки поверхностей называют приближенными.

Чтобы построить развертки неразвертывающихся поверхностей, эти поверхности разбивают на части, которые можно приближенно заменить развертывающимися поверхностями. После этого строят развертки этих частей, которые в сумме дают условную развертку неразвертывающейся поверхности.

2. Развертки пирамидальных и конических поверхностей

2.1 Определение натуральной величины элементов поверхностей

При развертывании поверхности на плоскости каждой точке поверхности соответствует единственная точка на развертке: линия поверхности переходит в линию развертки; длины линий, величины плоских углов и площадей, ограниченных замкнутыми линиями, остаются неизмеренными. Таким образом, процесс построения развертки сводится к отыскиванию натуральной (истинной) величины каждого элемента поверхности и изображению их на плоскости.

Каждая боковая грань на развертке (рис. 3) строится как треугольник по трем сторонам. CS -- самое короткое боковое ребро, поэтому рациональнее мысленно разрезать пирамиду по этому ребру.

Для нанесения на развертку точек D, Е и F, соответствующих вершинам сечения пирамиды плоскостью Sum, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники АBС и DEF, дающие истинную величину основания и сечения пирамиды.

2.2 Способ триангуляции. Построение развертки наклонного конуса

На рис. 4 способом триангуляции построена развертка конической поверхности, которая заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка представляет собой симметричную фигуру, так как поверхность имеет плоскость симметрии Sum. В этой плоскости лежит самая короткая образующая S-6. По ней и сделан разрез поверхности. Самая длинная образующая S-0 является осью симметрии развертки поверхности.

Натуральные величины образующих определены с помощью прямоугольных треугольников, как в предыдущей задаче на рис. 3. От оси симметрии S-0 строим шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников с общей вершиной S. Каждый из треугольников строим по трем сторонам, при этом две стороны равны истинным величинам образующих, а третья -- хорде, стягивающей дугу окружности основания между соседними точками деления.

Построенные на развертке точки О, 1, 2, ... соединяются. Построение развертки значительно упрощается, если поверхность представлена прямой пирамидой правильной формы или прямым круговым конусом

2.3 Построение развертки прямых пирамид

Построение ее упрощается тем, что образующая пирамиды AS и CS параллельны фронтальной плоскости проекций и на нее проецировались в натуральную величину. Основание же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости проекций, и на нее проецируется в натуральную величину. Для построения развертки достаточно построить сторону AS и сделать засечки радиусом дуги, равным BS и АВ из точек S и А, соответственно получим точку В и т. д. Основание же в натуральную величину можно построить на базе одной из его сторон, например АВ (рис. 5).

Положение точки на поверхности развертки пирамиды определим в следующем порядке: через фронтальную проекцию точки М (М2) проведем

горизонтальную линию до пересечения с ребрами A2S2 и B2S2. Получим точки 11 и 22. На линии AS развертки от точки А отложим отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD на которой нанесем точку М в том положении, которое она занимает на горизонтальной проекции линии 1, 2.

2.4 Построение развертки прямого кругового конуса

Рис. 6

На рис. 6 приведен пример построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса l на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки -- точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку. Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из точки M2 проведем горизонтальную линию до пересечения с очерковой образующей L и получим точку M2. Расстояние от основания конуса до точки M2 по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.

3. Развертки призматических и цилиндрических поверхностей

3.1 Способ нормального сечения. Построение полной развертки поверхностей треугольной призмы

Развертки призматических и цилиндрических поверхностей строят способом нормального сечения. Поверхность рассекают плоскостью, перпендикулярной ее образующим (ребрам), и определяют истинную величину нормального сечения. Линию нормального сечения развертывают в прямую. Тогда образующие (ребра) поверхности при развертке ее на плоскость располагаются перпендикулярно развертке линии нормального сечения, которую принимают за базу отсчета размеров образующих (ребер).

Рис.7

На рис. 7 построена полная развертка поверхностей треугольной призмы ABCDEF. Так как боковые ребра призмы BE, AD и CF параллельны плоскости П2, то они в истинную длину изображены на фронтальной плоскости проекций. Плоскость нормального сечения Sum(Sum2) является фронтально проецирующей. Нормальное сечение POR призмы построено в натуральную величину на плоскости П4, параллельной плоскости Sum и перпендикулярной плоскости П2. Линию нормального сечения разворачиваем в прямую и через точки Р, Q, R, и Р проводим прямые, перпендикулярные развертке линии нормального сечения. На каждом из построенных перпендикуляров откладывают по обе стороны от линии Р Р отрезки боковых ребер, измеренные на плоскости П2 (до нормального сечения и после него). Отмечаем точки ребер на развертке A и D, C и F, B и E соединяем их отрезками прямых, которые

дают истинную величину сторон основания призмы. Присоединяя к развертке боковой поверхности призмы оба основания (треугольники А В С и DEТ), получаем полную развертку призмы. На развертку призмы нанесена точка М, принадлежащая грани призмы ACFD, с помощью вспомогательной

прямой, параллельной ребрам призмы и пересекающей нормальное сечение в точке 1.

3.2 Построение развертки боковой поверхности эллиптического цилиндра. Способ нормального сечения

Рис. 8

На рис. 8 построена развертка боковой поверхности эллиптического цилиндра, в который для построения развертки вписана двенадцатиугольная призма. Поверхность имеет фронтальную плоскость симметрии. Самая длинная образующая -- нулевая, самая короткая -- шестая, по ней и сделан разрез поверхности. Развертка -- фигура симметричная относительно нулевой образующей. Истинная величина половины нормального сечения поверхности плоскостью Sum построена на плоскости П4 -- эллипс. Разворачиваем дугу полуэллипса в прямую 0 -- 6с помощью хорд 04--14, ... 54 -- 64, заменяющих кривые участки эллипса. В точках 0, 1, ... 6 на развертке восстанавливаем перпендикуляры, по которым откладываем натуральную длину участков, образующих поверхности (до нормального сечения и после него), измеренную на плоскости П2. Концы отрезков соединяем плавными кривыми, которые являются разверткой оснований поверхности. С помощью седьмой образующей на развертку нанесена точка поверхности.

3.3 Построение развертки призмы правильной формы

Построение разверток призматических и цилиндрических поверхностей значительно упрощается, если они представлены простыми прямыми фигурами.

Рис. 9

Для примера на рис. 9 приведена развертка трехгранной призмы правильной формы. Развертки ее строим, воспользовавшись тем, что ребра ее АА, ВВ, СС параллельны фронтальной плоскости проекций и проецируются на нее в натуральную величину, а нижнее ABC и верхнее А'В'С' основания параллельны горизонтальной плоскости проекций и проецируются на нее в натуральную величину. Точка М на развертке трехгранной призмы строится обычным способом.

3.4 Построение развертки прямого кругового цилиндра

Рис 10

На рис. 10 приведен пример построения развертки прямого кругового цилиндра. Ее высота Н на фронтальную плоскость проекций проецируется в натуральную величину, а нижнее и верхнее основания параллельны горизонтальной плоскости проекций и на нее проецируются в натуральную величину. В этом случае развертку цилиндрической поверхности строим с помощью хорд, соединяющих соседние точки деления окружности оснований, в который вписан правильный двенадцатиугольник. В этом случае цилиндрическая поверхность условно заменена поверхностью вписанной правильной двенадцатигранной призмы, и развертка цилиндрической поверхности построена способом триангуляции.

Положение точки М на развертке цилиндрической поверхности определяется обычным способом.

Аксонометрические проекции.

Чертёж, выполненный в прямоугольных (ортого­нальных) проекциях, является основным видом изобра­жения, которым пользуются в технике. Для облегчения пространственного представления о предмете иногда применяют аксонометрические проекции. Аксонометри­ческие проекции передают одним изображением про­странственную форму предмета. Такое изображение соз­даёт у человека впечатление, близкое к тому, которое получается при рассмотрении предмета в "натуре". Ак­сонометрические проекции получаются, если изобра­жаемый предмет вместе с осями координат, к которым он отнесён, с помощью параллельных лучей проецируют на одну плоскость, называемой аксонометрической.

Слово "аксонометрия" переводится "измерение по осям или измерения параллельно осям", так как размеры изображаемого предмета откладываются параллельно осям х, у, z называемым аксонометрическими осями. В зависимости от наклона осей координат х, у, z к аксо­нометрической плоскости и угла, составляемого проецирующими лучами с этой плоскостью, образуются раз­личные аксонометрические проекции. Если проецирую­щие лучи перпендикулярны плоскости, то проекция на­зывается прямоугольной. Если проецирующие углы наклонны к плоскости, то проекция называется косо­угольной.

предмет начертательной геометрии.

Начертательная геометрия теория изображения пространственных тел. Цель: изучение правил и способов для решения инженерных задач: создание новых чертежей и чтение уже созданных.

Разум человека уже владеет 3мя ключами открывающими всё: цифрой, буквой, нотой. Геометрия добавляет еще один ключ- линию.

Линия- язык графики, наиболее естественный язык для передачи информации. НГ- грамматика этого языка.