Построение точки встречи прямой с поверхностью многогранника
Для нахождения точек «входа-выхода» прямой на поверхности многогранника, нужно ввести дополнительную плоскость.
1. Заключить прямую в плоскость частного положения (плоскость α – горизонтально-проецирующая).
2. Сечение представляет собой треугольник 1,2,3, полученный при пересечении плоскостью α ребер многогранника AB, AS и AC.
3. Точки пересечения проекции треугольника 12,22,32 с проекцией прямой а2 (М2 и N2) на фронтальной плоскости проекций являются искомыми. Чтобы получить горизонтальные проекции этих точек, необходимо спроецировать их на а1 (М1 и N1).
4. По конкурирующим точкам определить видимость.
Построение развертки многогранной поверхности
Построение проводим по методу треугольников, так как многогранная поверхность состоит из граней, представляющих собой треугольники.
1. Основание пирамиды целиком расположено на горизонтальной плоскости проекций и уже имеет натуральную величину. Поэтому на свободном поле чертежа строим треугольник АВС, равный треугольнику А1В1С1 пунктирными линиями, так как это – линии сгиба.
2. Методом прямоугольного треугольника находим натуральную величину ребер SA, SB и SC.
3. К стороне АВ развертки достраиваем вершину S, для этого радиусом SA строим дугу из точки А, и радиусом SB – дугу из точки В.
4. Пересечение дуг и определит положение точки S.
5. Аналогично поступаем с гранями SАС и SBС.
Пример построения представлен на рисунке 90.
Точка на поверхности
Пирамида имеет в основании правильный многоугольник, вписанный в окружность диаметром 45 мм, и высоту 65 мм; в основании цилиндра и конуса лежат круги диаметром 45 мм, а их высоты – по 65 мм.
Вычертите пирамиду, цилиндр, конус в трех прямоугольных проекциях. Построение пирамиды начинайте с горизонтальной проекции, как проекции, обеспечивающей однозначное определение формы тела. При построении вначале используйте сплошные тонкие линии, и обведите линии видимых контуров сплошными основными линиями, а линии невидимых контуров – штриховыми линиями.
Во всех заданиях проекции точек указаны видимыми. Необходимо достроить недостающие проекции точек.
Если точка видимая и лежит на поверхности, спроецированной в линию, то она указывается буквой без скобок.
Если точка невидимая, т.е. закрыта от глаз наблюдателя какой-либо поверхностью, то она указывается буквой, взятой в скобки. Например, А - видимая проекция точки; (А) – невидимая проекция точки.
При построении проекций точек, принадлежащих поверхности пирамиды и конуса, следует применять способ, дающий наибольшую точность - способ образующей.
Пример построения представлен на рисунке 91.
 Рисунок 90
Рисунок 90
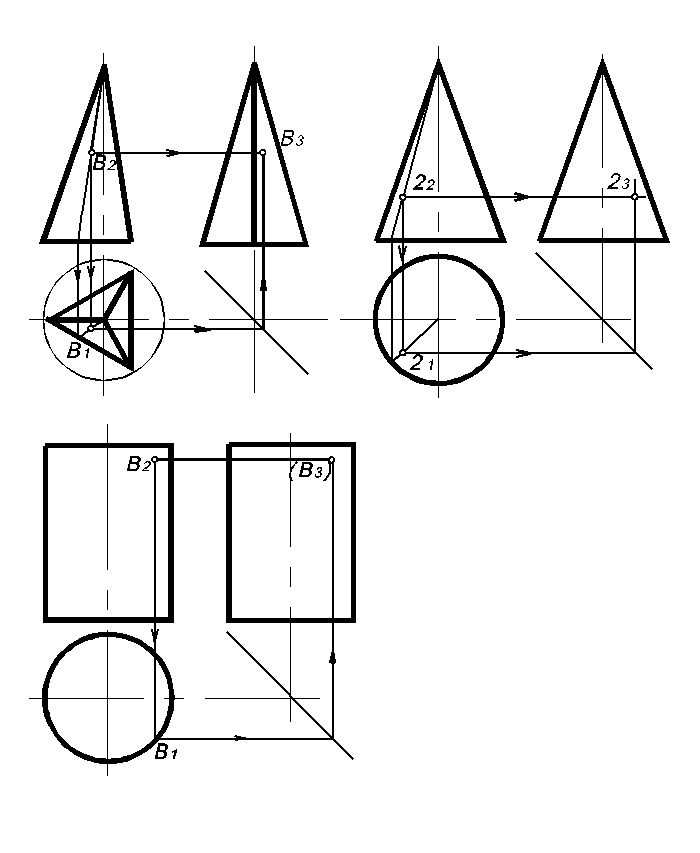
Рисунок 91
| № вар. | Xa | Ya | Za | Xb | Yb | Zb | Xc | Yc | Zc | Xd | Yd | Zd | Xe | Ye | Ze | Xk | Yk | Zk |
Список использованных источников
1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии.-М: «Наука», 1973- 368с.
2. Посвянский А.Д. Краткий курс начертательной геометрии.-М: «Высшая школа», 1970- 240с.
3. Фролов С.А. Начертательная геометрия.-М: «Машиностроение», 1983- 240с.
Лицензия №ЛР 020716 от 02.11.98
Формат 60х84 1/16 Бумага писчая.
Усл.печ.листов 2. Тираж 50. Заказ
Отпечатано в Оренбургском государственном университете
460352, г.Оренбург, ГСП, проспект Победы 13
ИПК ОГУ
