Виды аксонометрических проекций

Аксонометрические проекции в зависимости от направления проецирования разделяют на:

- косоугольные, когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;

- прямоугольные, когда направление проецирования перпендикулярно плоскости аксонометрических проекций.

В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:

- изометрия — все три коэффициента искажения равны между собой (u = v = w);

- диметрия — два коэффициента искажения равны между собой и отличаются от третьего (и не равно v = w или и= v не равно w);

- триметрия — все три коэффициента искажения не равны между собой (u не равно v не равно w).

Основное предложение аксонометрии сформулировано немецким геометром К. Польке: три произвольной длины отрезка прямых, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных координатных осях от начала.

Согласно этой теореме любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси. Любые произвольной длины отрезки этих прямых, отложенные от точки их пересечения, можно принять за аксонометрические масштабы.

Эта система аксонометрических осей и масштабов является параллельной проекцией некоторой прямоугольной системы координатных

осей и натуральных масштабов, т. е. аксонометрические масштабы можно выдавать совершенно произвольно, а коэффициенты искажения при этом связаны следующим соотношением: u² + v² = w² = 2 + + ctg²(p, где ф — угол между направлением проецирования и плоскостью аксонометрических проекций (рисунок 156). Для прямоугольной аксонометрии, когда ф = 90°, это соотношение принимает вид и² + v² + w² = 2 (1), т. е. сумма квадратов коэффициента искажения равна двум.

При прямоугольном проецировании может быть получена только одна изометрическая проекция и бесконечное множество диметрических и триметрических проекций. ГОСТ 2.317—69 предусматривает применение в инженерной графике двух прямоугольных аксонометрии: прямоугольной изометрии и прямоугольной диметрии с коэффициентами искажения и = w = 2v.

Прямоугольная изометрия

Прямоугольная изометрия характеризуется тем, что коэффициенты искажения составляют 0,82. Их получают из соотношения (1).

Для прямоугольной изометрии из соотношения (1) получаем:

Зu² = 2, или и = v - w = (2/3)^1/2 = 0,82, т. е. отрезок координатной оси

длиной 100 мм в прямоугольной изометрии изобразится отрезком аксонометрической оси длиной 82 мм. При практических построениях пользоваться такими коэффициентами искажения не совсем удобно, поэтому ГОСТ 2.317—69 рекомендует пользоваться приведенными коэффициентами искажения:

и = v = w — 1.

Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т. е. масштаб изображения в прямоугольной изометрии будет М^А1,22: 1.

Аксонометрические оси в прямоугольной изометрии располагаются под углом 120° друг к другу (рисунок 157). Изображение окружности в аксонометрии представляет интерес, особенно окружностей, принадлежащих координатным или им параллельным плоскостям.

В общем случае окружность проецируется в эллипс, если плоскость окружности расположена под углом к плоскости проекции (см § 43). Следовательно, аксонометрией окружности будет эллипс. Для построения прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.

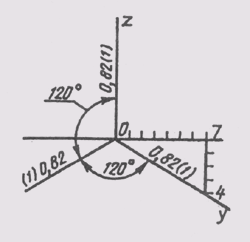
Рисунок 157 - Аксонометрические оси в прямоугольной изометрии

В прямоугольной изометрии равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы (рисунок 158).

Размеры осей эллипсов при использовании приведенных коэффициентов искажения равны: большая ось 2а= 1,22d, малая ось 2b = 0,71d, где d — диаметр изображаемой окружности.

Диаметры окружностей, параллельных координатным осям, проецируются отрезками, параллельными изометрическим осям, и изображаются равными диаметру окружности: l¹=l² =l³ = d, при этом l¹||x; l²||y; l³||z.

Эллипс, как изометрию окружности, можно построить по восьми точкам, ограничивающим его большую и малую оси и проекции диаметров, параллельных координатным осям.

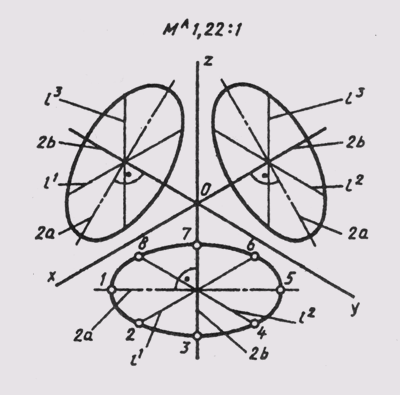
Рисунок 158 – Проецирование окружностей в прямоугольной изометрии

В практике инженерной графики эллипс, являющийся изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим такие же оси: 2a = 1,22d и 2b = 0,71 d. На рисунок 159 показано построение осей такого овала для изометрии окружности диаметра d (рисунок 159).

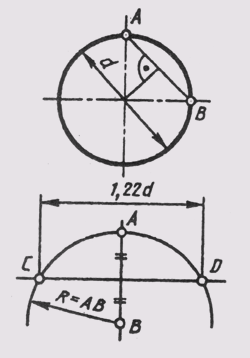
Рисунок 159 – Построение осей четырехцентрового овала для изометрии окружности

Для построения аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения, нужно выделить на окружности некоторое число точек, построить аксонометрию этих точек и соединить их плавной кривой; получим искомый эллипс— аксонометрию окружности (рисунок 160).

На окружности, расположенной в горизонтально проецирующей плоскости, взято 8 точек (1,2,... 8). Сама окружность отнесена к натуральной системе координат (рисунок 160, а). Проводим оси эллипса прямоугольной изометрии и, используя приведенные коэффициенты искажения, строим вторичную проекцию окружности 1¹₁,..., 5¹₁ по координатам х и у (рисунок 160, б). Достраивая аксонометрические координатные ломаные для каждой из восьми точек, получаем их изометрию (1¹, 2¹, ... 8¹). Соединяем плавной кривой изометрические проекции всех точек и получаем изометрию заданной окружности.

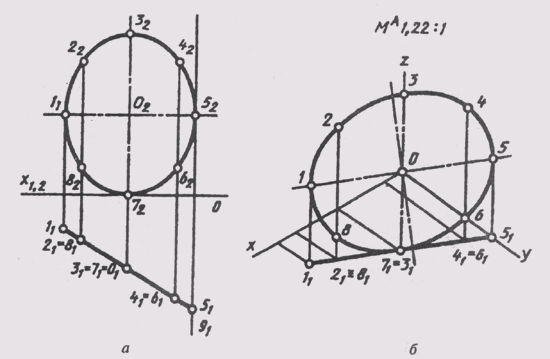
Рисунок 160 - Построение аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения

Изображение геометрических поверхностей в прямоугольной изометрии рассмотрим на примере построения стандартной прямоугольной изометрии усеченного прямого кругового конуса (рисунок 161).

На комплексном чертеже изображен конус вращения, усеченный горизонтальной плоскостью уровня, расположенной на высоте z от нижнего основания, и профильной плоскостью уровня, дающей в сечении на поверхности конуса гиперболу с вершиной в точке А. Проекции гиперболы построены по отдельным ее точкам.

Отнесем конус к натуральной системе координат Oxyz. Построим проекции натуральных осей на комплексном чертеже и отдельно их изометрическую проекцию. Построение изометрии начинаем с построения эллипсов верхнего и нижнего оснований, которые являются изометрическими проекциями окружностей оснований. Малые оси эллипсов совпадают с направлением изометрической оси О_Z(см. рисунок 158). Большие оси эллипсов перпендикулярны малым. Величины эллипсов осей определяются в зависимости от величины диаметра окружности (d — нижнего основания и d₁— верхнего основания). Затем строят изометрию сечения конической поверхности профильной плоскости уровня, которая пересекает основание по прямой, отстоящей от начала координат на величину X_A и параллельной оси О_у.

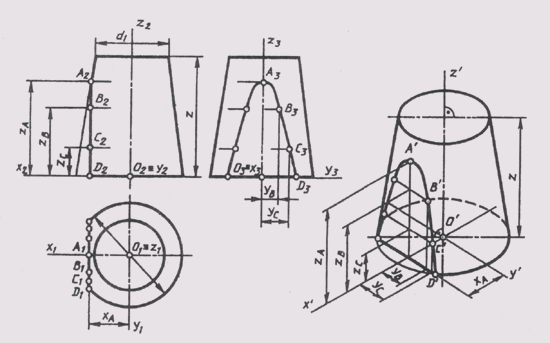
Рисунок 161 - Стандартная прямоугольная изометрия усеченного прямого кругового конуса

Изометрия точек гиперболы строится по координатам, замеряемым на комплексном чертеже, и откладываем без изменения вдоль соответствующих изометрических осей, так как приведенные коэффициенты искажения и = v = w = 1. Изометрические проекции точек гиперболы соединяем плавной кривой. Построение изображения конуса заканчивается проведением очерковых образующих касательной к эллипсам оснований. Невидимая часть эллипса нижнего основания проводится штриховой линией.

Прямоугольная диметрия

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:

u²+(u/2)²+u²=2;

u² =8/9; u = w = (8/9)^1/2=0,94; v = 0,47.

В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рисунке 162. Аксонометрический масштаб для прямоугольной диметрии будет М^A1,06 : 1.

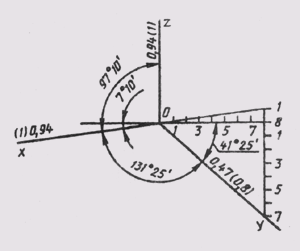
Рисунок 162 - Расположение осей стандартной прямоугольной диметрии

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а¹ = 1,066d, малая ось — 2b¹= 0,95d (рисунок 163). Диаметры. окружности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l¹ = l² = d; l = 0,5d, при этом || Ох; l²|| Оу; l³|| Oz.

Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.

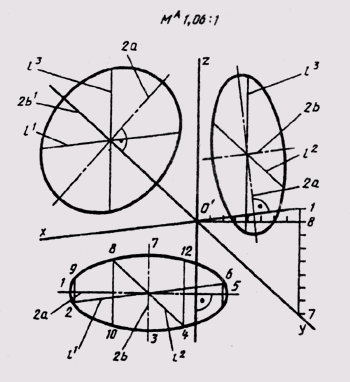
Рисунок 163 – Большая и малая оси в диметрии

Изображение геометрических поверхностей в прямоугольной диметрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рисунке 164 приведен пример комплексного чертежа полого цилиндра высотой Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.

Для наглядности построим вырез четверти цилиндра, построение которого видно из рисунке 164. Направление штриховки выреза выберем, как показано на рисунок 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.

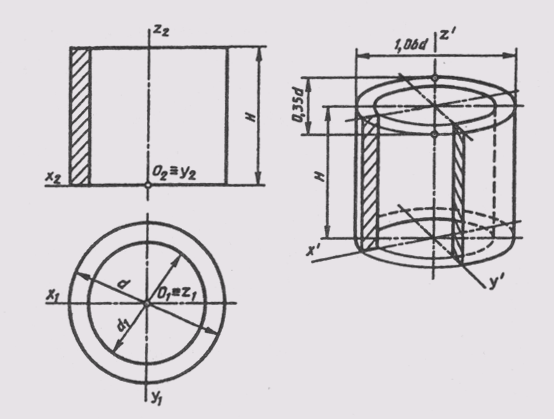
Рисунок 164 - Комплексный чертеж полого цилиндра

Вопросы для самопроверки

1 Как образуется аксонометрический чертеж?

2 Каково деление аксонометрических проекций в зависимости от направления проецирования?

3 Как располагаются оси в прямоугольной диметрии?

4 Чему раны большая и малая оси в изометрии и диметрии?