Особые случаи построения линии пересечения двух поверхностей вращения

При построении линии пересечения поверхностей вращения — конуса и цилиндра — могут быть различные случаи. На рисунке 136 изображены три случая пересечения цилиндра и конуса вращения. В первом случае (рисунок 136, а) цилиндр врезается в конус, потому что если вписать в конус сферу с центром в точке пересечения осей поверхностей, то радиус ее будет больше радиуса цилиндра. Все образующие цилиндра пересекаются с поверхностью конуса. Во втором (рисунок 136, б) конус врезается в цилиндр, так как сфера, вписанная в цилиндр, пересекает конус. Все образующие конуса пересекают поверхность цилиндра. В третьем (рисунок 136, в) сфера, вписанная в одну поверхность, касается второй поверхности, и в пересечении участвуют все образующие и цилиндра, и конуса. В этом случае пространственная линия пересечения поверхностей распадается на две плоские кривые (эллипсы).

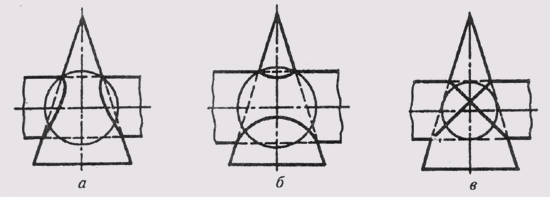
Рисунок 136 - Три случая пересечения цилиндра и конуса вращения

Это положение подтверждается теоремой Монжа: если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка, то они пересекаются по двум кривым второго порядка. Такие поверхности имеют две точки, в которых они касаются друг друга, или говорят, что поверхности имеют двойное прикосновение. Линия пересечения двух поверхностей вращения, имеющих двойное прикосновение, распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки прикосновения (рисунок 137). Две цилиндрические поверхности вращения одного диаметра касаются друг друга в точках А и В или имеют общие касательные, плоскости Ф¹ и Ф². Линия АВ занимает фронтально проецирующее положение, поэтому плоскости кривых пересечения будут фронтально проецирующими. Эллипсы ACBF и AEBD изображаются отрезками прямых на фронтальной плоскости проекций и окружностями, совпадающими с вырожденной проекций вертикального цилиндра, на горизонтальной плоскости проекций.

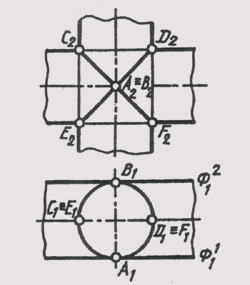
Рисунок 137 - Теорема Монжа

Это положение широко используется при изображении пересекающихся труб или отверстий одного диаметра (рисунок 138).

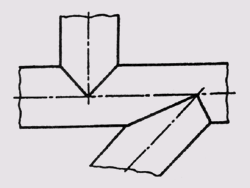
Рисунок 138 – Пересекающиеся трубы

В конструкциях технических деталей часто при пересечении поверхностей вращения используют сопрягающую поверхность, которая осуществляет плавный переход от одной поверхности к другой (рисунок 139, а, б, в).

Чтобы не строить две близко расположенные линии пересечения сопрягающей поверхности с основными поверхностями, на чертеже проводят условно одну линию, выполняя ее тонкой сплошной линией.

Эту линию и называют линией перехода. Линия перехода заканчивается в точках пересечения очерковых линий основных поверхностей (рисунок 139, а) и заменяется более простыми (циркульными) кривыми.

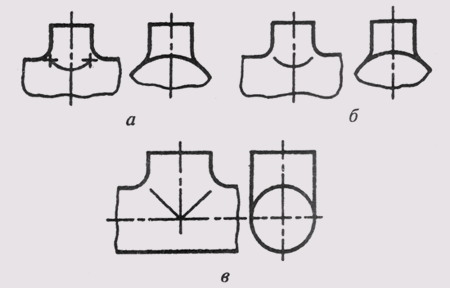
Рисунок 139 – Линии перехода

Вопросы для самоконтроля

1 Какие задачи называются позиционными?

2 Как определяется точка пересечения прямой с плоскостью?

3 Как строится линия пересечения двух плоскостей?

4 Что получается в сечении при пересечении поверхности с плоскостью?

5 Какая линия называется линией перехода и как она вычерчивается при изображении пересекающихся поверхностей?

6 В чем заключается способ вспомогательных поверхностей – посредников?

7 Что такое способ концентрических сфер?

Метрические задачи