Задача. Подземная дорога (поиск в ширину)
В некотором городе К-ске имеется свояподземная дорога. Администрация города решила построить новую кольцевую линию. "Центром" этого кольца должна стать одна из станций, при этом "радиус" такого кольца - минимальное кол-во станций, которое надо проехать, чтобы достичь кольцевой линии. То есть если радиус равен R - то кольцевая линия должна строиться на тех станциях, до которых можно добраться как минимум через R станций. Кольцо должно иметь как минимум две станции. Программа должна вывести все станции, через которые надо провести новую линию, или 0, если кольцо нельзяпостроить.
Формат входных данных
Первая строка содержит число N - количество станций метро (1<=N<=150) и число K. В следующих K строках содержится информация, описывающая схему. Сначала в строке идёт D - номер станции, затем число M, а далее - M чисел, которые показывают, с какими станциями соединена станция D.
В предпоследней строке - станция, которая будет "центром" станции, а в последней – радиус
кольца.
Формат выходных данных
На экран вывести номера искомых станций (в любом порядке). Если кольцо нельзя построить -
вывести 0.
Пример:
| input.txt | output.txt |
| 9 5 3 3 1 4 6 2 2 1 4 7 2 1 9 5 3 1 8 6 4 2 8 9 | 2 3 5 7 |
Графическоепредставлениепримера:
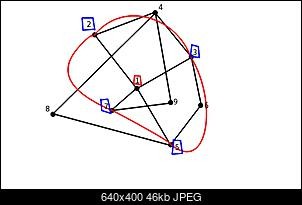
Решение: при помощи поиска в ширину (BFS) на k-ой итерации цикла мы будем находить все станции, до которых можно добраться как минимум через k станций. Сделав ограничение по R и записывая "уровень" каждой станции, мы определим все такие станции.
Код программы:
constMaxN = 100;
typeMatrix = array[1..MaxN,1..MaxN] ofboolean; //типматрицысмежности. M[i,j] = true, если станции i и j соединены.
Var
A : Matrix;
i, j, N, k, aa, bb, S, R, c: integer;
procedureBFS(A : Matrix; N, V, R : integer); //обход в ширину (V - корневаявершина)
vari, ps, pe : integer;
visited :array[1..MaxN] ofboolean; //массивпосещённостивершинq : array[1..MaxN] ofinteger; //"очередь" вершин
ql :array[1..MaxN] ofinteger; //и ихуровней.
begin//в качестве списка очередных вершин будем использовать структуру "очередь"
ps := 1; //начало очереди
pe := 1; //конец очереди
q[pe] := v; //в очередь помещается исходная вершина. На каждом шаге в очередь будем заносить всех преемников данной вершины (назовём их 1-го уровня, т.е. до которых можно дойти напрямую). Затем просматриваем в очереди занесённые ранее вершины 1-го уровня и добавляем в конец очереди вершины 2-го уровня и так далее до опустошенияочереди.
visited[v] := TRUE; //вершина V посещена
ql[ps] := 0; //сама вершина - нулевой уровень
while(ps<= pe) and(ql[ps] <R) do//пока очередь не пуста или не достигли необходимого уровня R
Begin
fori := 1 tondo if(A[v, i]) and(notvisited[i]) then
//перебираем все связные с V вершины
Begin
inc(pe); //и добавляем в очередь q[pe] := i;
ql[pe] := ql[ps] + 1; //отмечаем новый уровень преемника.
visited[i] := true; //отмечаем вершину I пройденной
end;
inc(ps); //переходим к следующей вершине в очереди v := q[ps]; //и делаем её корневой
end;
while(ql[ps] = R) and(ps<= pe) do//после работы цикла в очереди останутся только вершины, имеющие уровень R и более.
Begin
write(q[ps],' '); inc(ps);
end; end;
BEGIN
assign(input,'input.txt');
reset(input);
readln(input, N,c);
fori:=1 toc do begin
read(input, aa, k);
forj:=1 tok do begin
read(input, bb); A[aa, bb] :=true;
A[bb, aa] := true;
end; readln(input);
end;
readln(input, S); readln(input, R); close(input); BFS(A, N, S, R);
END.
Задача1
Для заданной строки символов проверить, является ли она симметричной или нет. (Симметричной считается строка, которая одинаково читается слева направо и справа налево).
Проще всего в этой задаче определить длину строки n, организовать цикл по номеру символа в строке и сравнивать попарно первый символ с последним, второй - с предпоследним и т.д. Если хотя бы одна пара различна, то строка не симметричная. Так как просматривается сразу пара символов, то в цикле будет m = n div 2 повторений. Для запоминания результата просмотра введем переменную k (k будет равна 0, если строка симметрична и 1 иначе).
Программа, решающая эту задачу, будет иметь вид:
var s:string;
i,k,n,m:integer;
begin
readln(s);
n:=length(s);
k:=0;
m:=n div 2;
for i:=1 to m do
if s[i]<>s[n-i+1] then k:=1;
if k=0 then writeln('Строка симметрична')
else writeln('Строка несимметрична');
end.
Задача 2
Для заданной строки символов вычислить произведение входящих в эту строку целых чисел (без учета их знаков). Например, для строки "kjjjkkj2.5jkjn,,,hfd45jgfvjlkfdii10,2hfhg" произведение 2*5*45*10*2=9000.
Пусть s - строка. Обозначим длину строки - l. Организуем цикл, в котором будем проверять, является ли очередной символ цифрой, если да, то организуем новый цикл, в котором будем формировать строку sn, состоящую из цифр (очередное целое число). Потом преобразуем sn в число и вычислим произведение. Программа на Паскале, реализующая данный алгоритм, будет иметь следующий вид (переменная p в этой программе используется для накапливания значения произведения, переменная kod - для хранения кода результата преобразования строки в число):
var sn,s:string;
l,k,kod:integer;
v,p:real;
begin
writeln('Введите строку');
readln(s);
l:=length(s);
p:=1; k:=1;
repeat
sn:='';
while (s[k]>='0')and(s[k]<='9')and(k<=l) do
begin
sn:=sn+s[k];
k:=k+1;
end;
if sn<>'' then
begin
val(sn,v,kod);
p:=p*v;
end;
k:=k+1;
until k>l;
writeln(' p=',p);
end.
Задача 3
Задана строка символов, содержащая два или более слов, разделенных пробелами. Написать программу, меняющую местами все четные и нечетные слова в строке, предполагая, что за один раз можно менять местами не более двух символов.
Решение
Имеется несколько путей решения этой задачи. Для упрощения предположим, что строка не начинается и не заканчивается пробелом и что между словами в строке стоит ровно по одному пробелу. Пусть известна пара слов, которую необходимо переставить, и - номера первой и последней букв в первом слове, и - номера первой и последней букв во втором слове. Рассмотрим способ, в котором для перестановки слов будем использовать следующий алгоритм:
Запишем буквы первого слова в обратном порядке (поменяв первую с последней, вторую с предпоследней и т.д.).
Например, из строки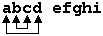 
получим dcba efghi.
Потом аналогичным образом переставим буквы второго слова:
из строки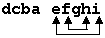 
получим dcba ihgfe.
Для получения окончательного результата необходимо записать буквы полученного словосочетания в обратном порядке:
Из строки 
получим efghi abcd (что и требовалось получить).
Таким образом, для перестановки двух слов достаточно написать подпрограмму, которая меняет в заданной строке порядок букв на противоположный (инвертирует строку), и вызвать эту подпрограмму для первого слова, второго слова и всего словосочетания.
Обозначим invert(k,l) - процедуру, которая записывает в заданной строке s символы с k-того по l-й в обратном порядке, тогда программа, решающая задачу, будет иметь вид:
var s:string;
i,n,m1,m2,l1,l2:byte;
procedure invert(k,l:byte);
var i:byte;
ch:char;
begin
for i:=k to ((l+k) div 2) do
begin
ch:=s[i];
s[i]:=s[l+k-i];
s[l+k-i]:=ch;
end;
end;
begin
writeln('Введите строку'); readln(s);
i:=0; n:=0;
m1:=1;m2:=1;l1:=1;l2:=1;
while i<length(s) do
begin
i:=i+1;
if (s[i]=' ')or(i=length(s)) then
begin
n:=n+1;
if n=1 then
begin
m2:=i-1;
l1:=i+1
end
else
begin
n:=0;
if i=length(s) then l2:=i else l2:=i-1;
invert(m1,m2);invert(l1,l2);invert(m1,l2);
m1:=i+1
end
end
end;
writeln(s)
end.
Лифт
Ограничения: время – 200мc, память - 64МБ
Петру необходимо попасть с этажа A на этаж B. Для вызова лифта на всех этажах офисного здания, кроме первого и последнего, есть две кнопки — для перемещения вниз и перемещения вверх. В тот момент, когда Петр нажал нужную кнопку вызова, лифт находился на этаже C и вез одного пассажира на этаж D. Если лифт проезжает мимо этажа, на котором нажата кнопка вызова, и лифт движется в подходящем направлении, то лифт останавливается, чтобы посадить дополнительного пассажира. Лифт перемещается между соседними этажами за одну единицу времени, также одну единицу времени занимает остановка лифта на этаже для высадки или посадки пассажиров.
Напишите программу, вычисляющую, через сколько времени Петр доберется до этажа B, при условии, что никто больше не будет вызвать лифт.
Первая строка ввода содержит четыре целых числа A, B, C и D, разделенных одним пробелом (1 ≤ A, B, C, D ≤20, A≠B, C≠D, A≠C).
Вывести одно целое число — количество единиц времени от момента вызова лифта до момента, когда Петр выйдет из лифта на этаже B.
Пример ввода 1 Пример вывода 1
3 9 2 5 10
Пример ввода 2 Пример вывода 2
3 9 5 2 13
Пояснение к примеру 1
Лифт за 1 единицу времени доедет до 3-го этажа, остановится на 1 единицу времени, чтобы Петр сел в лифт, затем через 2 единицы времени доедет до 5-го этажа и остановится на 1 единицу времени для высадки предыдущего пассажира, через 4 единицы времени лифт довезет Петра до 9-го этажа, и через 1 единицу времени Петр выйдет из лифта.
Решение
Нужно рассмотреть, движется ли лифт в том направлении, куда нужно Петру, будет ли он или пассажир лифта сходить на промежуточном этаже, и вывести формулы для этих вариантов.
Существует 4 варианта:
1) пассажир едет на этаж, где находится Петр;
2) Петр едет в том же направлении, что и лифт, и лифт может посадить его по пути, Петр выходит раньше или одновременно с пассажиром лифта;
3) тоже что и 2, но пассажир выходит раньше Петра;
4) лифт сначала отвозит пассажира, затем отвозит Петра.
Пример реализации:
uses math;
var a,b,c,d:integer;
begin
read(a,b,c,d);
if d=a then
writeln(abs(c-d)+1+abs(a-b)+1)
else if not((a<b)xor(c<d)) and (a>=min(c,d)) and (a<=max(c,d)) then
begin
if (b>=min(c,d)) and (b<=max(c,d)) then
writeln(abs(c-a)+1+abs(a-b)+1)
else
writeln(abs(c-a)+1+abs(a-d)+1+abs(d-b)+1);
end
else
writeln(abs(c-d)+1+abs(d-a)+1+abs(a-b)+1);
end.
Задача
Для любого целого числа N>7 найти все такие пары целых чисел x и y, что 3x+5y=N.
Разделим N нацело на 5 и получим k - максимальное значение для y (т.е. 0<=y<=k). Организуем цикл по переменной y , и будем рассматривать значения разности N-5y. Если это число делится нацело на 3, то полученное частное и есть соответствующее значение x.
Решение
var x,y,n,k:integer;
begin
writeln('Введите N');
readln(n);
k:=n div 5;
for y:=0 to k do
if (N-5*y) mod 3=0 then
begin
x:=(N-5*y) div 3;
writeln('x=',x,' y=',y);
end;
end.
Задача REBUS
Составить программу REBUS, которая определяет все 4-значные числа на интервале [M, N], удовлетворяющие условиям:
a) abcd - 4-значное число;
b) a, b, c, d - разные цифры;
c) ad - cd = a + b + c + d;
и подсчитывает общее количество этих чисел.
Во входном файле REBUS.DAT в 1-й и 2-й строчках находятся два числа M и N. В файле REBUS.SOL выводятся числа, удовлетворяющие условиям а)-с), и их количество.
| файл REBUS.DAT | файл REBUS.SOL |
Решение
program REBUS;
var a,b,c,d,m,n,k,i:integer; f:text;
begin
assign (f,'rebus.dat');
reset(f);
readln(f,m,n);
close(f);
assign(f,'rebus.sol');
rewrite(f);
for i:=m to n do
begin
a:=i div 1000;
b:=i mod 1000 div 100;
c:=i mod 100 div 10;
d:=i mod 10;
if (a <> b) and (a <> c) and (a <> d) and (b <> c) and (b <> d) and (c <> d) and (a*d-c*d=a+b+c+d) then
begin
k:=k+1;
append(f);
writeln(f,i);
end;
end;
append(f);
writeln(f,k);
close(f)
end.
Задача “Эчпочмаки”
С приближением холодов любимая крыса Василия Федоровича решила готовить запасы на зиму. На ее радость, Василий Федорович неожиданно решил продемонстрировать свое кулинарное мастерство и приготовил N эчпочмаков, оставив их на некоторое время без присмотра.
В системе жизненных ценностей крысы эчпочмак определяется как треугольник, заданный длинами своих сторон (ввиду отсутствия кулинарного мастерства у Василия Федоровича эчпочмаки получались в виде произвольных невырожденных треугольников). Основное качество эчпочмака по логике крысы — это его площадь (чем больше площадь, тем более ценен эчпочмак).
Крыса была бы рада утащить себе в гнездо, свитое в полости дивана, самый ценный эчпочмак целиком, но прогрызенная ею щель имеет ограниченные размеры, и туда могут пролезть не все эчпочмаки. Щель задается своей шириной D (вещественное число) в сантиметрах. Эчпочмак может быть ориентирован произвольно в плоскости отверстия, и если хотя бы в одном положении он проходит в щель, то он считается подходящим.
Необходимо найти номер наиболее ценного эчпочмака, который проходит в отверстие.
Формат входных данных
Во входном файле записано целое число N — количество эчпочмаков (1 Ј N Ј 1000) и вещественное число D (с точностью до 4 знаков после точки, 0 < D Ј 1000). Далее записаны N троек вещественных чисел Ai, Bi, Ci, задающих длины сторон эчпочмаков (с точностью до 4 знаков после точки, 0 < Ai, Bi, Ci Ј 1000).
Формат выходных данных
В выходной файл выведите номер наиболее ценного эчпочмака, который проходит в щель. Если существует несколько различных правильных ответов, то выведите любой из них. В случае, если ни один эчпочмак протащить невозможно, выведите 0.
Пример
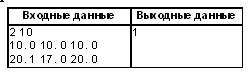
Комментарий к примеру:
Решение
Введем ось x, направленную перпендикулярно прямой, содержащей отверстие. Произвольно ориентируем треугольник в плоскости и начнем двигать его вдоль оси x. Введем функцию d(x), значение которой равно длине отрезка, лежащего в треугольнике на прямой, содержащей отверстие.
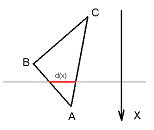
Несложно доказать, что с момента прохода вершины A и до момента достижения вершины B функция d(x) будет возрастающей, а затем, до вершины C — убывающей (при доказательстве можно воспользоваться подобием треугольников). Из этого следует, что своего максимума функция d(x) достигнет, когда точка B (средняя вершина треугольника) будет лежать на прямой. То есть, чтобы проверить, проходит ли треугольник при такой ориентации сквозь отверстие, достаточно посчитать значение функции d(x) в средней вершине и проверить, что оно не больше размеров отверстия.
Определимся с наилучшей ориентацией треугольника. Один конец отрезка, задающего пересечение прямой и треугольника, является средней вершиной этого треугольника, а второй лежит на противоположной стороне треугольника. Кратчайшее расстояние от вершины треугольника до его противоположной стороны — это высота этого треугольника. Отсюда понятно, что треугольник надо ориентировать так, чтобы его наименьшая высота была параллельна прямой, содержащей отверстие.
Для вычисления площади треугольника можно воспользоваться формулой Герона
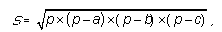
где a, b, c — длины сторон треугольника, а p — его полупериметр. Длину наименьшей высоты можно вычислить, пользуясь формулой для площади треугольника S = 1/2•h•a, где a — наибольшая сторона. То есть h = 2•S/a, где a — наибольшая сторона.
Для решения задачи просто перебираем все треугольники и запоминаем номер треугольника с наибольшей площадью, у которого минимальная высота не больше размеров отверстия.
vari, n, bestno: longint;
a, b, c, p, s, d, h, bests: double;
Begin
read(n, d); bestno := 0; bests := -1;
for i := 1 to n do begin
read(a, b, c);
p := (a + b + c) / 2;
s := sqrt(p*(p-a)*(p-b)*(p-c));
if b > a then a := b;
if c > a then a := c; h := 2*s/a;
if (h <= d) and (s > bests) then begin
bestno := i; bests := s
End
end;
write(bestno)
end.
Задача “Ниточка”
Злоумышленники варварски вбили в ни в чем неповинную плоскую поверхность N гвоздей, да так, что только шляпки остались. Мало того, они в своих подлых целях вбили все гвозди в вершины выпуклого многоугольника. После этого они... страшно сказать... они натянули ниточку вокруг всех гвоздей, так, что поверхности стало совсем грустно!
Ваша задача — определить длину этой ниточки.
Формат входных данных
В первой строке находятся два числа — количество гвоздей N, 1 < N < 100, и вещественное число R — радиус шляпок гвоздей. Все шляпки имеют одинаковый радиус. Далее располагаются еще N строк, в каждой из которых записана через пробел пара вещественных координат центра очередного гвоздя; координаты не превосходят по абсолютной величине числа 100. Описания гвоздей приводятся в порядке обхода вершин многоугольника по или против часовой стрелки, начиная с произвольного гвоздя. Шляпки разных гвоздей не соприкасаются.
Формат выходных данных
Вывод должен в своей единственной строке содержать вещественное число, округленное до двух знаков после точки, — длину ниточки, натянутой вокруг всех гвоздей.
Пример
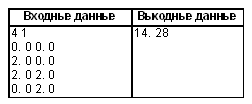
Решение:
Сначала рассмотрим случай, когда радиус шляпок равен нулю. Тогда нам достаточно просто просуммировать расстояния между всеми последовательными гвоздями (не забыв соединить последний с первым). Расстояние между точками с номерами k и m равно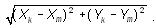 
. Теперь посмотрим, как будет вести себя длина ниточки, когда у шляпок появится ненулевой радиус.
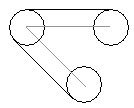
Длина части веревочки, не соприкасающейся со шляпкой, будет равна длине веревочки, соединяющей центры гвоздей. Это объясняется тем, что каждый участок между двумя гвоздями лежит на касательной к двум последовательным окружностям (вместе с отрезком, соединяющим центры, и радиусами он образует прямоугольник). Таким образом, нам остается найти длину той части ниточки, которая соприкасается со шляпками, и просуммировать эти числа.
Для каждой из окружностей рассмотрим угол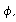 
вершиной которого является центр окружности, а на сторонах лежат точки касания. Длина ниточки, соприкасающейся со шляпкой, будет равна 
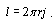. Суммарный же угол по всем гвоздям будет равен 
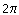, так как многоугольник выпуклый и радиус вектор, задающий положение ниточки, совершает полный оборот.
Отсюда следует, что к сумме расстояний между центрами шляпок следует прибавить число 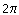r.
vari, n : longint;
r, s : double;
x, y : array[0..100] of double;
Begin
read(n, r);
s := 2*pi*r;
for i := 0 to n - 1 do
read(x[i], y[i]);
for i := 0 to n - 1 do
s := s + sqrt(sqr(x[i] — x[(i + 1) mod n]) +
sqr(y[i] — y[(i + 1) mod n]));
write(s:0:2)
end.
В реализации использовалась нумерация элементов массива с нуля, чтобы сделать его “закольцованным” и не обрабатывать отдельно последнюю и первую вершины.
Задача “Обезьяны”
Есть две обезьяны и куча из L бананов. Обезьяны по очереди, начиная с первой, берут из кучи бананы, причем 1-ая обезьяна может при каждом очередном ходе взять из кучи либо a1, либо a2, либо ... aS бананов (а1 <a2 <...<aS), а 2-ая при каждом очередном
ходе --либо b1, либо b2, либо ... bK бананов (b1 <b2 <...<bK ). Нумерация индексов при a и b не имеет никакого отношения к номерам ходов обезьян Выигрывает та обезьяна, которая на своем ходе не может взять банан(ы) (либо потому, что их не осталось, либо потому что бананов осталось меньше чем a1 (при ходе первой обезьяны) либо b1 (при ходе второй обезьяны)).
Определить может ли выиграть первая обезьяна при наилучших ходах соперницы, которая также стремится выиграть. Все входные данные - натуральные числа.
Решение
Будем обозначать текущую ситуацию в игре парой (S,i), где S количество бананов, оставшихся в куче, перед текущим ходом i-ой обезьяны (i равно 1 или 2).
Для того, чтобы (S,1) была выигрышной для игрока 1, среди возможных ситуаций после его хода (S-a1,2), ... ,(S-ak,2) должна быть хоть одна проигрышная для игрока 2 (в эту то ситуацию и надо будет перевести игру); если все ситуации выигрышные для игрока 2, то (S,1) - проигрышная для игрока 1 (как бы он не поступал, он все равно проиграет).
Пусть ситуация после хода игрока 1 стала (S',2). Опять же делаем все допустимые ходы из этой позиции и смотрим является ли получившаяся ситуация (S",1) выигрышной, проигрышной или такой, которую мы еще не можем оценить. Если выполняется последняя альтернатива, то из (S",1) мы опять делаем все возможные ходы, анализируем, и т.д.
Если мы в конце концов определили, для кого является выигрышной текущая позиция, то возвращаемся к предыдущему ходу и пытаемся определить, какая позиция для делающего ход и т. д., пока не вернемся к ситуации (L,1).
const l1=200;
s=10;
var a: array [0..l1,1..2] of byte; {в ячейке a[L,i]
хранится информация, кто выигрывает в ситуации (L,i)}
b: array [1..2,0..s] of byte; {массив возможных ходов
первого и второго игроков в b[i,0] хранится число
возможных ходов игрока i}
l,i,j:integer;
Function f(ba:Integer;No: Byte): Byte;
Var i,p,r: Byte; {рекурсивная функция вычисления (L,i)}
Begin {f=i, если в (ba,i) выигрывает i}
if Ba<0 {после хода монет <0?}
Then f:= 3-No {выигрыш игрока с номером 3-Nо}
else if ba=0 {монет = 0?}
then begin {выигрыш No}
f:=No;
a[ba,no]:=no;
end
Else if a[ba,no]<>0 {в этой ситуации мы уже были}
Then F := a[ba,no] {в ней выигрывает a[ba,no]}
Else
Begin {эту ситуацию мы еще не рассматривали}
r := 0;
{мы будем делать все возможные ходы}
For i := 1 to b[No,0] do
if ba-b[no,i]>=0 {если ход возможен, то делаем его}
then r := r or F(Ba-B[No,i],3-No);
if r=0 then r:=no;
If (No and R)<>0 {есть выигрышный ход?}
Then p := No {да, (ba,i)=No}
Else p := 3-No; {нет, (ba,i)=3-No}
A[Ba,No]:=p; {запоминаем эту информацию}
f:=p;
End;
end;
begin
for i:=0 to l1 do
for j:=1 to 2 do A[i,j] := 0;
write('s=');
readln(b[1,0]); {b[1,0] = количество ходов первого игрока}
for i:=1 to b[1,0] do
begin
write('a',i,'='); {сами ходы}
Readln(b[1,i]);
end;
write('k=');
Readln(b[2,0]); {b[2,0] = количество ходов второго игрока}
For j := 1 to b[2,0] do
begin
write('b',j,'=');
Readln(b[2,j]); {ввод ходов}
end;
repeat {для данных ходов вводятся значения L}
write('L='); {число бананов}
readln(l);
if f(l,1)=1 {вызов рекурсивной функции-проверки}
then writeln('1-я выиграла')
else writeln('1-я проиграла');
for i:=1 to b[1,0] do {распечатка результатов возможных ходов}
if (l-b[1,i])>=0 {из начальной позиции L}
then writeln('b=',b[1,i],' winner=',a[l-b[1,i],2]);
writeln;
until false;
end.
Задача Интересное число
Имя входного файла input.txt
Имя выходного файла output.txt
Максимальное время работы на одном тесте: 2 секунды
Для заданного числа n найдите наименьшее положительное целое число с суммой цифр n, которое делится на n.
Формат входных данных.
Во входном файле содержатся целое число n (1 ≤ n ≤ 1000).
Формат выходных данных.
Выходной файл должен содержать искомое число. Ведущие нули выводить не разрешается.
Пример
| input.txt | output.txt |
Код программы:
program Number;
const max = 1 shl 12;
inf = 1 shl 30;
y = 10;
var
a: array[0..max - 1, 0..max] of boolean;
b, c: array[0..max - 1, 0..max] of integer;
red: array[0..max - 1, 0..y - 1] of integer;
qx, qy, s: array[0..max * (max + 1) - 1] of integer;
front, rear, n, u, v, k, i, j: integer;
begin
reset(input, 'input.txt');
rewrite(output, 'output.txt');
read(n);
for i := 0 to n - 1 do
for j := 0 to y - 1 do
red[i][j] := (i * y + j) mod n;
for i := 0 to n - 1 do
for j := 0 to n do
a[i][j] := false;
a[0][0 ] := true;
qx[0] := 0;
qy[0] := 0;
front := 0;
rear := 1;
while front < rear do
begin
i := qx[front];
j := qy[front];
inc(front);
if (i = 0) and (j = n) then
begin
i := 0;
j := n;
k := 0;
while j > 0 do
begin
u := b[i][j];
v := c[i][j];
s[k] := j -v;
inc(k);
i := u;
j := v;
end;
for i := k -1 downto 0 do write(s[i]);
writeln;
exit
end;
for k := 0 to y - 1 do
begin
u := red[i][k];
v := j + k;
if v > n then break;
if not a[u][v] then
begin
a[u][v] := true;
b[u][v] := i;
c[u][v] := j;
qx[rear] := u;
qy[rear] := v;
inc(rear);
end;
end;
end;
assert(false);
end.