Комментарии к решению задачи.
Основная идея решения данной задачи основана на переборе всех перестановок цифр числа a. Чтобы это сделать, обозначим полученное число aperm. Теперь, для того, чтобы найти число bperm, которое необходимо получить перестановкой цифр числа b, достаточно вычесть из числа c число aperm. Для проверки возможности перестановки цифр числа b таким образом, чтобы получилось число bperm, предлагается проверить на равенство мультимножества цифр указанных чисел. Это можно сделать, например, посчитав количество нулей, единиц, двоек … девяток в каждом из сравниваемых чисел.
type
tDigits= array[1..10] of byte;
var
la,lb,ld: integer;
da,db,dd: tDigits;
a,b,c,r: longint;
procedure Swap(var a,b: byte);
var
x: byte;
begin
x:= b;
b:= a;
a:= x
end;
procedure Digits(x: longint; var dx: tDigits; var lx: integer);
var
i,j: integer;
begin
lx:= 0;
while x>0 do begin
inc(lx);
dx[lx]:= x mod 10;
x:= x div 10
end;
for i:=2 to lx do for j:=lx downto i do if dx[j]>dx[j-1] then Swap(dx[j],dx[j-1])
end;
procedure Permutations(x: tDigits; l: integer);
var
i: integer;
begin
if l=0 then begin
Digits(c-r,dd,ld);
if ld=lb then begin
i:=1;
while (i<=lb) and (dd[i]=db[i]) do inc(i);
if i>lb then begin
writeln('YES');
writeln(r,' ',c-r);
readln;
halt
end
end
end
else for i:=l downto 1 do begin
Swap(x[i],x[l]);
r:= r*10+x[l];
Permutations(x,l-1);
r:= r div 10;
Swap(x[i],x[l])
end
end;
begin
readln(a,b,c);
Digits(a,da,la);
Digits(b,db,lb);
Permutations(da,la);
writeln('NO');
readln
end.
Элементы вычислительной геометрии
Две окружности
(Время: 1 сек. Память: 16 Мб)
На плоскости даны две окружности. Требуется проверить, пересекаются ли они.
Входные данные
Входной файл INPUT.TXT состоит из двух строк. На каждой строке записана информация об одной окружности – координаты ее центра x и y (целые числа, по модулю не превосходящие 5000) и радиус (целое число 1 ≤ r ≤ 1000).
Выходные данные
В выходной файл OUTPUT.TXT выведите «YES», если окружности пересекаются, и «NO» в противном случае.
Примеры
| № | INPUT.TXT | OUTPUT.TXT |
| 0 0 2 0 3 2 | YES | |
| 1 1 1 4 4 1 | NO |
РЕШЕНИЕ:
Что бы решить данную задачу необходимо знать:
— Алгоритмы ветвления
Для решения задачи, в первую очередь, нам необходимо найти расстояние между двумя центрами окружностей, с помощью формулы расстояния между двумя точками 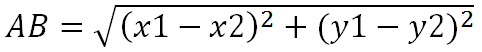
Рассмотрим варианты размещения окружности:
1. Если пересечений бесконечно много, тогда, как видно с рисунка, центры окружности совпадают, то есть расстояние между ними равно нулю и равны между собой радиусы.
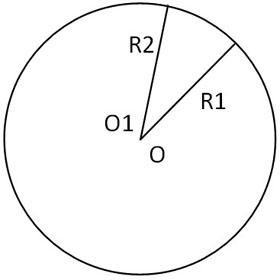
2. Если пересечение происходит только в одной точке, тогда возможны 2 варианта:
a. Расстояние между центрами окружностей ОО1 равно разности по модулю двух радиусов (ОО1=|R1-R2|)
b. Расстояние между центрами окружностей ОО1 равно сумме двух радиусов (ОО1=R1+R2)
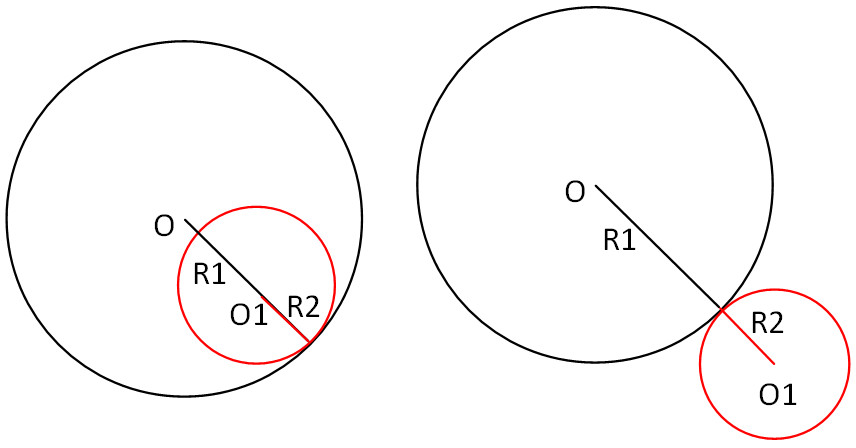
3. Если пересечение окружностей нет, тогда есть 2 варианта:
a. Расстояние между центрами окружностей ОО1 меньше разности по модулю двух радиусов (ОО1<|R1-R2|) b. Расстояние между центрами окружностей ОО1 больше сумме двух радиусов (ОО1>R1+R2)
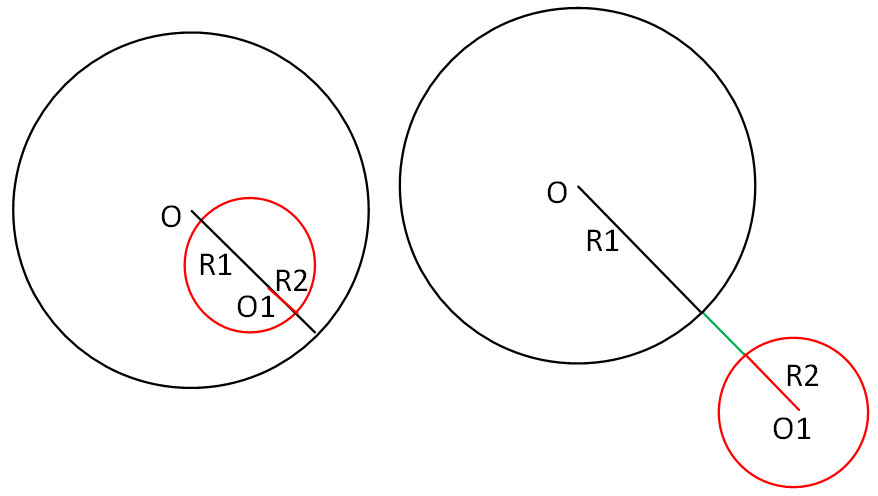
4. Ну и последний вариант, если ни один из выше перечисленных не подходит, тогда окружность пересекается в двух точках.
Полный текст решение задачи «Две окружности» с помощью Pascal будет иметь вид:
var r1,r2,x1,x2,y1,y2,r:real;
begin
assign (input,'input.txt'); reset (input);
assign (output,'output.txt'); rewrite (output);
read(input,x1,y1,r1,x2,y2,r2);
r:=sqrt(sqr(x2-x1)+sqr(y2-y1));
if (r1+r2>=r)and(r1+r>=r2)and(r2+r>=r1)
then write('YES')
else write('NO');
end.
