Задача 1. Замечательные числа
Задача 1. Замечательные числа
ограничение по времени: 1 сек
входной файл input.txt
выходной файл output.txt
Условие задачи:
Назовем целое число N замечательным, если для него справедливо равенство (*)
N²=(N – 1)² + M², где М – целое число. Даны два целых числа А и В. Найти количество замечательных чисел из диапазона [A,B] включительно. Например, в диапазоне [1,10] таких чисел два, а именно числа 1 и 5.
Входные данные: во входном файле input.txt содержатся два целых числа А и В (1<=A<=B<=109), разделенных пробелом.
Выходные данные: в выходной файл output.txt записать количество замечательных чисел из заданного диапазона.
Пример:
| input.txt | output.txt |
| 1 10 |
Решение:
Эта задача на сокращение перебора. Если просто пробежать отрезок от А до В, то мы не успеем по времени. Значит надо сокращать перебор.
Упрощаем равенство (*), получим 2*N-1= M² . В левой части этого равенства находится нечетное число, следовательно, М тоже нечетное и принадлежит отрезку от 1 до квадратного корня из числа 2*N-1. Так как максимальное значение N равно В, то правая граница отрезка, содержащего М равна квадратному корню из числа 2*1000000000-1. Увеличим ее и возьмем равную квадратному корню из числа 2*1000000000. А это число меньше 50000 и можно перебирать.
program zad1;
var m,a,b,n:integer;
kol:integer; input,output:text;
begin
Assign(input,'input.txt');
Reset(input);
Assign(output,'output.txt');
rewrite(output);
read(a,b);
kol:=0;
for m:=1 to trunc(sqrt(2000000000)) do {перебираем М}
if m mod 2 = 1 then {если М нечетное}
begin
n:=(m*m+1) div 2; {вычисляем N}
if (n>=a)and(n<=b) then inc(kol); {проверяем принадлежность N отрезку }
end;
writeln(kol);
close(input); close(output);
end.
Тесты к задаче: в архиве «Задача 1»
Задача 2. Острова
входной файл input.txt
выходной файл output.txt
Каждый элемент квадратной матрицы размеренности N x N равен нулю, либо единице. Найдите количество «островов», образованных единицами. Под «островом» понимается группа единиц (либо одна единица), со всех сторон окруженная нулями (или краями матрицы). Единицы относятся к одному «острову», если из одной из них можно перейти к другой «наступая» на единицы, расположенные в соседних клетках. Соседними являются клетки, граничащие по горизонтали или вертикали.
Входные данные
В первой строке файла input.txtзаписано натуральное число N не больше 100 - размер квадратной матрицы. В следующих N строках задаются элементы матрицы через пробел.
Выходные данные
В файл output.txtвыведите единственное число - количество островов.
Пример
| input.txt | output.txt |
| 5 1 0 1 1 1 0 0 0 0 0 1 1 1 0 1 0 1 0 0 1 0 0 0 1 1 |
Решение задачи
Итак, это классическая задача на поиск в глубину графа. Понятно, что надо обходить матрицу и каким-то образом вычислять количество островов. Вариант решения такой: после того, как мы попадаем на остров, надо это зафиксировать увеличив переменную-результат на единицу. Чтобы второй раз не посчитать один и тот же остров, сразу после посещения необходимо его уничтожить, т.е. присвоить всем клеткам острова значение ноль.
Поскольку тест задачи не слишком мал, стоит написать процедуру уничтожения островов, назовем ее"count". Чтобы во время выполнения процедуру не "выскочить" за пределы массива, сделаем его не размером N x N, а размеров N+2 x N+2, это даст нам возможность окружить искомый массив размером N x N нулями.
const m = 102;var a:array [1..m, 1..m] of integer; i,j,n,res: integer; input,output: text;procedure count(i,j: integer);begin if a[i,j] <> 1 then exit; a[i,j] := 0; count(i + 1, j); count(i - 1, j); count(i, j + 1); count(i, j - 1); end;begin res:= 0; assign(input,'input.txt'); reset(input); assign(output,'output.txt'); rewrite(output); read(input, n); {Заполняем массив нулями} for i:= 1 to n+2 do for j:=1 to n+2 do a[i,j]:=0; {Считываем матрицу из файла} for i:= 2 to n+1 do forj:=2 to n+1do read(input,a[i,j]); {Обходим матрицу в поиске островов} for i := 2 to n+1 do for j := 2 to n+1 do if a[i,j] = 1 then begin inc(res); count(i,j); end; write(output,res); close(input); close(output);end.Тесты к задаче: в архиве «Задача 2»
Задача 3 Клавиатура
Всем известно, что со временем клавиатура изнашивается, и клавиши на ней начинают залипать. Конечно, некоторое время такую клавиатуру еще можно использовать, но для нажатий клавиш приходиться использовать большую силу.
При изготовлении клавиатуры изначально для каждой клавиши задается количество нажатий, которое она должна выдерживать. Если знать эти величины для используемой клавиатуры, то для определенной последовательности нажатых клавиш можно определить, какие клавиши в процессе их использования сломаются, а какие – нет.
Требуется написать программу, определяющую, какие клавиши сломаются в процессе заданного варианта эксплуатации клавиатуры.
Формат входных данных
Первая строка входного файла содержит целое число n (1 ≤ n ≤ 100) – количество клавиш на клавиатуре. Вторая строка содержит n целых чисел – с1, с2, … , сn, где сi (1 ≤ сi ≤ 100000) – количество нажатий, выдерживаемых i-ой клавишей. Третья строка содержит целое число k (1 ≤ k ≤ 100000) – общее количество нажатий клавиш, и последняя строка содержит k целых чисел pj (1 ≤ pj ≤ n) – последовательность нажатых клавиш.
Формат выходных данных
В выходной файл необходимо вывести n строк, содержащих информацию об исправности клавиш. Если i-ая клавиша сломалась, то i-ая строка должна содержать слово“yes” (без кавычек), если же клавиша работоспособна – слово“no”.
Пример входных и выходных данных
| input.txt | output.txt |
| 5 1 50 3 4 3 161 2 3 4 5 1 3 3 4 5 5 5 5 5 4 5 | yes no no no yes |
Краткие методические рекомендации по решению задачи
Решение данной задачи заключается в следующем. В первую очередь необходимо для каждой клавиши на клавиатуре посчитать количество нажатий на нее и проверить, больше ли оно некоторого числа. Количество нажатий клавиш можно хранить в массиве и, считывая очередное нажатие, увеличивать счетчик для данной клавиши. После считывания всех нажатий для всех клавиш следует последовательно проверить выполнение указанного в описании задачи условие.
Программная реализация решения этой задачи требует аккуратности при чтении входных данных и при выводе выходных данных. Кроме этого, требуется аккуратно организовать хранение информации о числе нажатий в одномерном массиве.
Таким образом, чтобы набрать полный балл, требуется реализовать простейшее линейное решение, в котором используются лишь базовые операции с массивами.
Возможные ошибки
Можно применить "лобовое" решение, т.е. создать два или три массива, но на самом деле нужен только один размером 100 элементов. При лобовом решении необходим массив в 100000 элементов, а создать его в Turbo Pascal не удастся. Самое интересное, что лобовое решение проходит если использовать компилятор Free Pascal. При решении задачи надо обратить внимание, что в выходной файл данные надо выводит в нижнем регистре.
Текст программы на Паскале одного из участников олимпиады:
Var c : array [1..100] of longint; n, i, k, t : longint; f : text;input,output: text;Begin Assign(f,'input.txt'); Reset(f); ReadLn(f,n); For i:=1 to N do Read(f,c[i]); Readln(f,k); For i:=1 to k do beginRead(f,t); Dec(c[t]); end; Close(f); Assign(f, 'output.txt'); Rewrite(f); For i:=1 to N do If c[i]>=0 Then Writeln(f,'no') Else Writeln(f,'yes'); Close(f);End.Задача 4 . Вырубка деревьев
| Имя входного файла: input.txt Имя выходного файла: output.txt Максимальное время работы на одном тесте: 1 секунда Максимальный объем используемой памяти: 64 мегабайта |
Король Флатландии решил вырубить некоторые деревья, растущие перед его дворцом. Деревья перед дворцом короля посажены в ряд, всего там растет N деревьев, расстояния между соседними деревьями одинаковы.
После вырубки перед дворцом должно остаться M деревьев, и расстояния между соседними деревьями должны быть одинаковыми. Помогите королю выяснить, сколько существует способов вырубки деревьев.
Требуется написать программу, которая по заданным числам N и M определит, сколько существует способов вырубки некоторых из N деревьев так, чтобы после вырубки осталось M деревьев и соседние деревья находились на равном расстоянии друг от друга.
Формат входных данных
Входной файл INPUT.TXT содержит два целых числа M и N (0 <= M <= N <= 1000).
Формат выходных данных
В выходном файле OUTPUT.TXT должно содержаться одно число - искомое количество способов.
Пример входных и выходных данных
| input.txt | output.txt |
| 5 3 |
Краткие методические рекомендации по решению задачи
Зафиксируем расстояние между деревьями после вырубки. Если оно равно d, то возможно
n – d(m – 1) – m + 1 способов вырубить деревья. Суммируя по всем d, получаем ответ.
Если у нас есть 0 деревьев и 0 деревьев должно остаться после вырубки, то существует один вариант вырубки - это надо учитывать при решении задачи.
Вариант 1 (с использованием цикла)
var n, m : longint; i, d, s : longint; input, output: text;begin Assign(input,'input.txt'); Reset(input); Assign(output,'output.txt'); Rewrite(output); Read(input,n,m); s := 0; if m = 0 then s := 1 else if m = 1 then s := n else for d := 1 to (n-1) div (m-1) do inc(s,n-(m-1)*d); Write(output,s); Close(input); Close(output);end.Вариант 2 (без цикла)
var n, m ,k: longint; i, d, s : longint; input, output: text;beginAssign(input,'input.txt'); Reset(input); Assign(output,'output.txt'); Rewrite(output); read(input,n,m); if m=0 then s:=1 else if m=1 then s:=n else begin k:=(n-1) div (m-1);{количество членов прогрессии} d:=m-1;{шаг прогрессии} s:=(2+(k-1)*d)*k div 2;{формула суммы первых членов арифметической прогрессии} end; write(output, s); Close(input); Close(output);end.Тема: Сортировка и поиск.
Задание
Напишите программу, которая по заданным координатам деревень и количеству почтовых отделений находит такое расположение почтовых отделений по деревням, при котором общая сумма расстояний от каждой деревни до её ближайшего почтового отделения будет минимальной.
Входные данные
Первая строка входного файла POST.DAT содержит два целых числа: первое число – количество деревень V, 1≤V≤300, второе число – количество почтовых отделений P, 1≤P≤30, P≤V. Вторая строка содержит V целых чисел в возрастающем порядке, являющихся координатами деревень. Для каждой координаты X выполняется 1≤X≤10000.
Выходные данные
Первая строка выходного файла POST.SOL содержит одно целое число S – общую сумму расстояний от каждой деревни до её ближайшего почтового отделения для расположения почтовых отделений, описанного во второй строке. Вторая строка содержит P целых чисел в возрастающем порядке. Эти числа являются искомыми координатами почтовых отделений. Если для заданного расположения деревень есть несколько решений, то программа должна найти одно из них.
Пример входных и выходных данных
| POST.DAT | POST.SOL |
| 10 5 1 2 3 6 7 9 11 22 44 50 | 9 2 7 22 44 50 |
ОЦЕНКА РЕШЕНИЯ
Если выходной файл не соответствует описанным требованиям – оценка 0. В противном случае, оценка будет вычислена по таблице 1 следующим образом: если найденная сумма – S, а минимальная сумма – Smin, то необходимо вычислить q=S/Smin и найти соответствующую оценку c в нижней строке.
| q=S/Smin | q=1.0 | 1.0<q≤1.1 | 1.1<q≤1.15 | 1.15<q≤1.2 | 1.2<q≤1.25 | 1.25<q≤1.3 | 1.3<q |
| c |
Решение
Program POST;
const MaxN = 350;
var k, n, p: integer;
x: array [1..MaxN] of integer;
d, t: array [1..MaxN] of longint;
pr: array [1..MaxN, 1..35] of integer; {объявление массивов}
procedure ReadAll;{процедура связи с файлом вход. данных и записи в файл}
var i: integer;
begin
Assign(input, 'post.dat'); Reset(input);
Assign(output, 'post.sol'); Rewrite(output);
Read(n, p);
for i := 1 to n do read(x[i]); {цикл перебора элементов массива}
end;
procedure Solve; {основная процедура решения задачи}
var i, j, r, m: integer;
min, s: longint;
begin
fillchar(d, sizeof(d), 0); {заполняем строку нулями}
for i := 1 to n do begin
s := 0;
for j := 1 to i-1 do inc(s, longint(x[i])-longint(x[j]));{увеличиваем значение переменной s и преобразовываем элементы массива в длинное целое}
d[i] := s;
end;
for k := 2 to p do begin
for i := 1 to N do begin
t[i] := 1000000000;
r := i; {запись координат деревень }
s := 0;
for j := i-1 downto 1 do
begin
while (r > j) and (x[i]-x[r-1] < x[r-1]-x[j]) do begin {координаты почты }
dec(r);
s := s - (longint(x[r]) - longint(x[j+1])) +
(longint(x[i]) - longint(x[r]));
end;
inc(s, longint(r-j-1) * (longint(x[j+1])-longint(x[j])));
if s + d[j] < t[i] then begin
t[i] := s + d[j];
pr[i, k] := j;
end;
end;
end;
d := t;
end;
min := maxlongint;
for i := 1 to n do begin {вычисление минимального расстояния}
s := d[i];
for j := i+1 to n do inc(s, longint(x[j])-longint(x[i]));
if s < min then begin
min := s;
m := i;
end;
end;
writeln(min);
k := p;
while k > 0 do begin
d[k] := m;
m := pr[m, k];
dec(k);
end;
for i := 1 to p-1 do write(x[d[i]], ' ');
writeln(x[d[p]]);
end;
begin
ReadAll;
Solve;
end.
Задача 2: Светофоры
В подземелье M тоннелей и N перекрестков, каждый тоннель соединяет какие-то два перекрестка. Мышиный король решил поставить по светофору в каждом тоннеле перед каждым перекрестком. Напишите программу, которая посчитает, сколько светофоров должно быть установлено на каждом из перекрестков. Перекрестки пронумерованы числами от 1 до N.
Формат входных данных
Формат выходных данных
Пример
| input.txt | output.txt |
| 7 10 | 3 3 2 2 5 2 3 |
| 5 1 | |
| 3 2 | |
| 7 1 | |
| 5 2 | |
| 7 4 6 5 6 4 7 5 2 1 5 3 |
Решение
Program Svetofor;
var n, i, j, k : longint;
a : array [1..100] of integer;
b : array [1..5000, 1..2] of integer;
num : char;
t : integer;
f : text;
procedure swap (var a, b : integer); {замена}
var t : integer;
begin
t := a;
a := b;
b := t;
end;
begin
for num := '1' to '9' do begin
randomize; {случайным образом формируем матрицу}
writeln('Test #', num, ', n = ');
readln(n);
fillchar(a, sizeof(a), 0);
k := 0;
for i := 1 to n do
for j := 1 to i - 1 do
if random(MaxInt) >MaxInt div 2 then begin
inc(a[i]);
inc(a[j]);
inc(k);
b[k, 1] := i;
b[k, 2] := j;
end;
for i := 1 to k do begin
j := random(k)+1;
t := random(k)+1;
swap(b[t, 1], b[j, 1]);
swap(b[t, 2], b[j, 2]);
end;
assign(f, 'y_' + num + 'input.txt');
rewrite(f);
writeln(f, n, ' ', k);
for i := 1 to k do
writeln(f, b[i, 1], ' ', b[i, 2]);
close(f);
assign(f, 'y_' + num + 'output.txt');
rewrite(f);
for i := 1 to n do
write(f, a[i], ' ');
writeln(f);
close(f);
end;
end.
Тема: Метод перебора вариантов.
Задача 3: Зернышки
Имя входного файла: Input.txt.
Имя выходного файла: Output.txt.
В банке находятся белые и черные зернышки. Каждый раз из банки вынимают наугад два зернышка. Если они одинакового цвета, то их выбрасывают, а в банку кладут черное зернышко (черных зернышек достаточное количество). Если же зернышки разного цвета, то черное зернышко выбрасывают, а белое возвращают в банку. Эти действия повторяют, пока не останется одно зернышко.
Задание.Напишите программу, которая по известному количеству черных и белых зернышек определяет цвет последнего зернышка.
Входные данные.В единственной строке записаны два числа – количество белых и черных зернышек.
Выходные данные. Единственная строка выходного текстового файла должна содержать цвет оставшегося зернышка: white – если зернышко белое, black – если зернышко черное.
Пример входных и выходных данных:
| Input.txt | Output.txt |
| 4 3 | black |
program grain;
var white, black:longint;
begin
assign(input, 'input.txt');
reset(input);
assign(output, 'output.txt');
rewrite(output);
read(white, black);
if odd(white) then writeln('white') else {проверка чётности числа}
writeln('black');
close(input);
close(output);
end.
Задача 4: Простые гири
Существуют гири массой 1 г, 2г, …, N г (N ≤ 500000). Напишите программу, которая распределяет эти гири на максимально возможное количество пар, так чтобы общий вес гирь в каждой паре выражался простым числом.
Формат входящих данных: входной файл Input.txt содержит одно число N.
Формат выходящих данных: в выходной файл Output.txt выведите список найденных пар, по одной паре в ряду.
Решение
Program Prost_g;
var N:LongInt;
Procedure Read_data; {Процедура чтения начальных данных }
begin
assign(Input, 'Input.txt');
reset(Input);
readln(N);
close(Input)
end;
Function Prost(x:LongInt): Boolean; {Функция определения, является ли число простым}
var
q:Boolean;
i:LongInt;
begin
q:=False;
if Odd(x) then
begin
q:=True;
i:=3;
while (i*i<=x) and q do
if x mod i=0 then q:=False
else inc(i,2)
end;
Prost :=q
end; {End Prost}
Procedure Solve_Write; {Процедура поиска и записи «простых» пap}
var
flag:Boolean;
i, j : LongInt;
begin
assign(Output, 'Output.txt');
rewrite(Output);
repeat
i:=l;
while not Prost(n+i) do inc(i);
j:=i-l;
while i<n do
begin
writeln(i, ‘ ‘ ,n);
inc(i);
dec(n)
end;
n:=j
until n<=l;
close(Output)
end; {End Solve_Write}
BEGIN
Read_Data;
Solve_Write;
END.
Тема: Метод перебора вариантов.
Задача 5: Покупка билетов
Имя входного файла: Input.txt.
Имя выходного файла: Output.txt.
Максимальное время работы на одном тесте: 5 секунд.
Максимальный объем использованной памяти: 4 Мбайты.
За билетами на премьеру нового мюзикла собралась очередь из N лиц, каждое из которых хочет купить 1 билет. На всю очередь работала только одна касса, потому продажа билетов продвигалась очень медленно, от чего «клиенты» очереди впадали в отчаяние. Самые сообразительные быстро приметили, что, как правило, несколько билетов в одни руки кассир продает быстрее, чем когда эти же билеты продаются по одному. Поэтому они предложили нескольким людям, которые стоят рядом, отдавать деньги первому из них, чтобы он купил билеты на всех.
Но для борьбы со спекулянтами кассир продавала не больше 3-х билетов в одни руки, потому договориться таким образом между собой могли лишь 2 или 3 лица, которые стоят рядом.
Известно, что на продажу ілицу из очереди одного билета кассир тратит Аі секунд, на продажу двух билетов – Вісекунд, трёх билетов – Сi секунд.
Задание. Напишите программу, которая определит минимальное время, за которое можно было бы обслужить всех покупателей.
Обратите внимание, что билеты на группу людей, которые объединились, всегда покупает первый из них. Также никто с целью ускорения не покупает лишние билеты (то есть билеты, которые никому не нужные).
Входные данные.Первая строка входного файла содержит единственное число N – количество покупателей в очереди (1£N£5000). В каждой из следующих N строк записана тройка натуральных чисел Аі, Bi, Сi. Каждое из этих чисел не превышает 3600. Люди в очереди нумеруются, начиная от кассы
Выходные данные. Исходный файл содержит одно число – минимальное время в секундах, за которое можно было бы обслужить всех покупателей.
Пример входных и выходных данных
| Input.txt | Output.txt |
| 5 10 15 | |
| 2 10 15 | |
| 5 5 5 | |
| 20 20 1 | |
| 20 1 1 | |
| 3 4 5 | |
| 1 1 1 |
Решение
program buying_tickets;
const size=5000;
var
a, b, c: array [1..size] of integer;
time: array [1..size of longint;
n:integer;
procedure read_data; {процедура считающая количество людей в очереди}
var i:integer;
begin
assign(input, 'input.txt');
reset(input);
readln(n);
for i:=1 to n do readln(a[i], b[i], c[i]);
close(input);
end;
function min(x,y:longint:longint);
begin
if x<y then min:=x else min:=y;
end;
procedure solv; {процедура подсчитывает время продажи билетов}
var i:integer;
begin
time[1]:=a[1];
time[2]:=min(a[1]+a[2], b[1]);
time[3]:=min(time[2]+a[3], min(a[1]+b[2], c[1]));
for i:=4 to n do
time[i]:=min(time[i-1]+a[i], min(time[i-2]+b[i-1],
time[i-3]+c[i-2]));
end;
procedure write_data; {запись результатов в файл}
begin
assign(output, 'output.txt');
rewrite(output);
writeln(time(n));
close(output);
end;
begin
read_data;
solve;
write_data;
end.
Оглавление
Работа с большими числами. 2
Сортировка и поиск. 5
Метод перебора вариантов, отсечения перебора. 8
Элементы вычислительной геометрии. 11
Эффективные структуры данных. 14
Работа с большими числами
Золото племени АББА
(Время: 1 сек. Память: 16 Мб Сложность: 40%)
Главный вождь племени Абба не умеет считать. В обмен на одну из его земель вождь другого племени предложил ему выбрать одну из трех куч с золотыми монетами. Но вождю племени Абба хочется получить наибольшее количество золотых монет. Помогите вождю сделать правильный выбор!
Входные данные
В единственной строке входного файла INPUT.TXT записаны три натуральных числа через пробел. Каждое из чисел не превышает 10100. Выходные данные
В выходной файл OUTPUT.TXT нужно вывести одно целое число – максимальное количество монет, которые может взять вождь.
Примеры
| № | INPUT.TXT | OUTPUT.TXT |
| 5 7 3 987531 234 86364 189285 283 4958439238923098349024 |
РЕШЕНИЕ:
Для решения данной задачи необходимо знать темы:
— работа со строками
— обработка одномерных массивов
— длинная арифметика
Из условия задачи видно, что числовые данные 10100 выходят за все возможные стандартные типы в Free Pascal. Поэтому для решения задачи будем использовать длинную арифметику. Если внимательно посмотреть, можем заметить, что нам необходимо будет найти наибольшее число среди трех куч с золотыми монетами.
Формат входных данных. Числа представлены в одну строку, поэтому для начала нам необходимо будет их преобразовать к нашему удобному виду.
readln(f,s);
ReadLong(A,copy(s,1,pos(‘ ‘,s)-1));
delete(s,1,pos(‘ ‘,s));
ReadLong(B,copy(s,1,pos(‘ ‘,s)-1));
Также для вывода результата, нам необходимо будет написать свою процедуру вывода длинных чисел WriteLong. Сначала будем находить первый не нулевой разряд и его записывать в файл
k:=high(d);
while (k>1)and(d[k]=0) do dec(k);
write(f1,d[k]);
Далее добавляя передние нули (при необходимости, если количество цифр не равно нашему представлению разряда числа) будем выводить все остальные элементы массива (наше число) в обратном порядке.
for i:=k-1 downto 1 do
begin
str(d[i],s);
for j:=length(s)+1 to len do
s:=’0’+s;
write(f1,s);
end;
Полный текст программы выглядит так:
const base=10000;len=4;
type TLong=array [1..26] of LongInt;
var a,b:TLong;
f,f1:Text;
k:Integer;
s:string;
{Процедура считывания числа}
procedure ReadLong(var d:TLong;s:string);
var k,error,i:Integer;
begin
for i:=1 to high(d) do
d[i]:=0;
for i:=(length(s) mod len)+1 to len do
s:=’0’+s;
k:=0;
while len*k< length(s) do
begin
inc(k);
val(copy(s,length(s)-len*k+1,len),d[k],error);
// delete(s,length(s)-len+1,len);
end;
end;
{Процедура сравнения длинных чисел}
function Compare(number1,number2:Tlong):Integer;
var i:Integer;
begin
i:=high(number1);
while (i>1)and(number1[i]=number2[i]) do dec(i);
if number1[i]>number2[i] then Compare:=1
else if number1[i]=number2[i] then Compare:=0
else Compare:=-1;
end;
{Процедура вывода на экран длинного числа}
procedure WriteLong(d:TLong);
var i,k,j:Integer;
s:string;
begin
k:=high(d);
while (k>1)and(d[k]=0) do dec(k);
write(f1,d[k]);
for i:=k-1 downto 1 do
begin
str(d[i],s);
for j:=length(s)+1 to len do
s:=’0’+s;
write(f1,s);
end;
writeln(f1);
end;
begin
assign(f,’input.txt’);
reset(f);
assign(f1,’output.txt’);
rewrite(f1);
readln(f,s);
ReadLong(A,copy(s,1,pos(‘ ‘,s)-1));
delete(s,1,pos(‘ ‘,s));
ReadLong(B,copy(s,1,pos(‘ ‘,s)-1));
delete(s,1,pos(‘ ‘,s));
if Compare(A,B)=-1 then A:=B;
ReadLong(B,s);
if Compare(A,B)>-1 then WriteLong(A)
else WriteLong(B);
close(f1);
close(f);
end.
Упрощенная (время 0,122, память 1164 Кб)
var s,t,p:string;
f:text;
i:integer;
begin
assign(f,'input.txt');
s:='';
reset(f);
read(f,t);
t:=t+' ';
for i:=1 to 3 do
begin p:=copy(t,1,pos(' ',t));
delete(t,1,length(p));
if length(p)>length(s) then s:=p;
if (length(p)=length(s))and(p>=s) then s:=p end;
close(f);
assign(f,'output.txt');
rewrite(f);
write(f,s);
close(f)
end.
Сортировка и поиск
2. Домашнее задание.
Петя успевает по математике лучше всех в классе, поэтому учитель задал ему сложное домашнее задание, в котором нужно в заданном наборе целых чисел найти сумму всех положительных элементов, затем найти где в заданной последовательности находятся максимальный и минимальный элемент и вычислить произведение чисел, расположенных между ними. Так же известно, что минимальный и максимальный элемент встречаются в заданном множестве чисел только один раз. Поскольку задач такого рода учитель дал Пете около ста, то Петя как сильный программист смог написать программу, которая по заданному набору чисел самостоятельно находит решение. А Вам слабо?
Входные данные
В первой строке входного файла INPUT.TXT записано единственное число N – количество элементов массива. Вторая строка содержит N целых чисел, представляющих заданный массив. Все элементы массива разделены пробелом. Каждое из чисел во входном файле не превышает 102 по абсолютной величине.
Выходные данные
В единственную строку выходного файла OUTPUT.TXT нужно вывести два числа, разделенных пробелом: сумму положительных элементов и произведение чисел, расположенных между минимальным и максимальным элементами. Значения суммы и произведения не превышают по модулю 3*104.
Примеры:
| № | INPUT.TXT | OUTPUT.TXT |
| 6 -3 5 7 9 0 5 | 26 35 | |
| 8 1 2 3 4 5 6 7 8 | 36 5040 | |
| 5 8 7 5 -3 2 | 22 35 |
РЕШЕНИЕ
Данная задача решается с помощью классических алгоритмов обработки данных в массиве. Во первых, стоит вычислить сумму всех положительных элементов, которые находятся в массиве. Для этого пройдемся по всем значениям и к значениям суммы будем прибавлять только те элементы, которые больше «0» (то есть, положительные).
Sum:=0;
for i:=1 to n do
if a[i]>0 then Sum:=Sum+a[i];
Далее, согласно условия, нам необходимо найти индексы наибольшего и наименьшего значения элементов в массиве. Введем две переменные minId, MaxId, которые соответственно содержат значения номеров маленького и самого элементов линейной таблицы. Если среди просмотренных элементов мы найдем большее значение, чем то значение, которое мы считали начальным - мы изменим номер индекса максимального элемента
if a[i]>a[MaxId] then MaxId:=i;
Аналогично с минимальным:
if a[i]<a[MinId] then MinId:=i;
Зная позицию нахождения наибольшего и наименьшего элементов, мы можем найти произведение чисел, расположенных между ними:Mult:=1;
for i:=MinId+1 to MaxId-1 do
Mult:=Mult*a[i];
begin
x:=MaxId;
MaxId:=MinId;
MinId:=x;
end;
Полный текст программы «Домашнее задание»:
var f,f1:text;
n,i,minId,MaxId,x,Sum,Mult:Integer;
a:array[1..100] of Integer;
begin
assign(f,’input.txt’);
reset(f);
assign(f1,’output.txt’);
rewrite(f1);
{Считывание данных}
readln(f,n);
for i:=1 to n do
read(f,a[i]);
Sum:=0;
for i:=1 to n do
if a[i]>0 then Sum:=Sum+a[i];
minId:=1;
{ Считаем, что минимальный элемент находится на первой позиции}MaxId:=1;
{ Считаем, что максимальный элемент находится на первой позиции}for i:=2 to n do
begin
if a[i]>a[MaxId] then MaxId:=i;
if a[i]<a[MinId] then MinId:=i;
{Если мы нашли меньше элемент чем считали минимальным, меняем индекс минимального}
end;
{Изменение индексов расположения крупнейшего элемента и наименьшего}
if MaxId<MinId then
begin
x:=MaxId;
MaxId:=MinId;
MinId:=x;
end;
{Нахождение произведения между минимальным и максимальным значением элементов массива}
Mult:=1;
for i:=MinId+1 to MaxId-1 do
Mult:=Mult*a[i];
{Вывод результата}
writeln(f1,Sum,’ ‘,Mult);
close(f);
close(f1);
end.
Метод перебора вариантов, отсечения перебора
3. Сумма двух чисел
Заданы три числа: a, b, c. Необходимо выяснить, можно ли так переставить цифры в числах a и b, чтобы в сумме получилось c.
Формат входных данных
Входной файл содержит три целых числа: a, b, c (0 < a, b, c < 109). Числа разделены пробелом.
Формат выходных данных
Если искомая перестановка цифр возможна, необходимо вывести в выходной файл слово YES, в противном случае — выведите слово NO. При положительном ответе необходимо вывести во второй строке выходного файла число x, получаемое перестановкой цифр числа a, и число y, получаемое перестановкой цифр числа b, сумма которых равна c. Числа x и y не должны содержать ведущих нулей. Числа в строке разделены пробелом.
Примеры входных и выходных файлов
| Input2.txt | output2.txt |
| 12 31 25 | YES 12 13 |
| 12 31 26 | NO |
Две окружности
(Время: 1 сек. Память: 16 Мб)
На плоскости даны две окружности. Требуется проверить, пересекаются ли они.
Входные данные
Входной файл INPUT.TXT состоит из двух строк. На каждой строке записана информация об одной окружности – координаты ее центра x и y (целые числа, по модулю не превосходящие 5000) и радиус (целое число 1 ≤ r ≤ 1000).
Выходные данные
В выходной файл OUTPUT.TXT выведите «YES», если окружности пересекаются, и «NO» в противном случае.
Примеры
| № | INPUT.TXT | OUTPUT.TXT |
| 0 0 2 0 3 2 | YES | |
| 1 1 1 4 4 1 | NO |
РЕШЕНИЕ:
Что бы решить данную задачу необходимо знать:
— Алгоритмы ветвления
Для решения задачи, в первую очередь, нам необходимо найти расстояние между двумя центрами окружностей, с помощью формулы расстояния между двумя точками 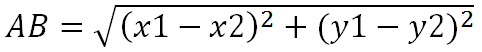
Рассмотрим варианты размещения окружности:
1. Если пересечений бесконечно много, тогда, как видно с рисунка, центры окружности совпадают, то есть расстояние между ними равно нулю и равны между собой радиусы.
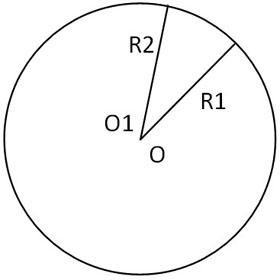
2. Если пересечение происходит только в одной точке, тогда возможны 2 варианта:
a. Расстояние между центрами окружностей ОО1 равно разности по модулю двух радиусов (ОО1=|R1-R2|)
b. Расстояние между центрами окружностей ОО1 равно сумме двух радиусов (ОО1=R1+R2)
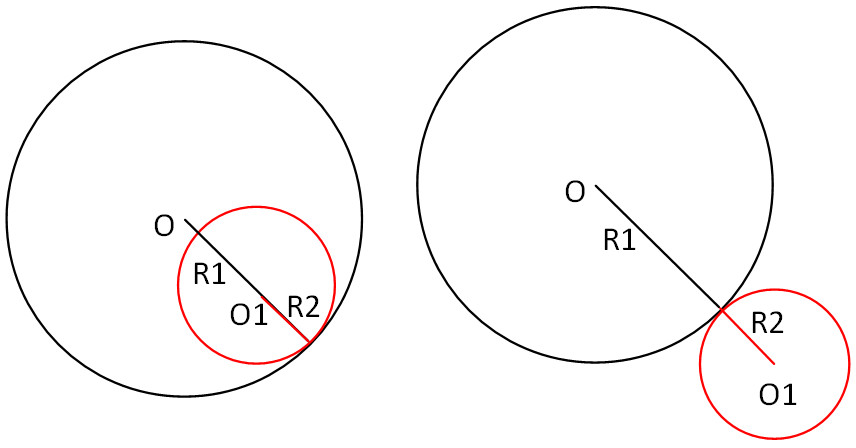
3. Если пересечение окружностей нет, тогда есть 2 варианта:
a. Расстояние между центрами окружностей ОО1 меньше разности по модулю двух радиусов (ОО1<|R1-R2|) b. Расстояние между центрами окружностей ОО1 больше сумме двух радиусов (ОО1>R1+R2)
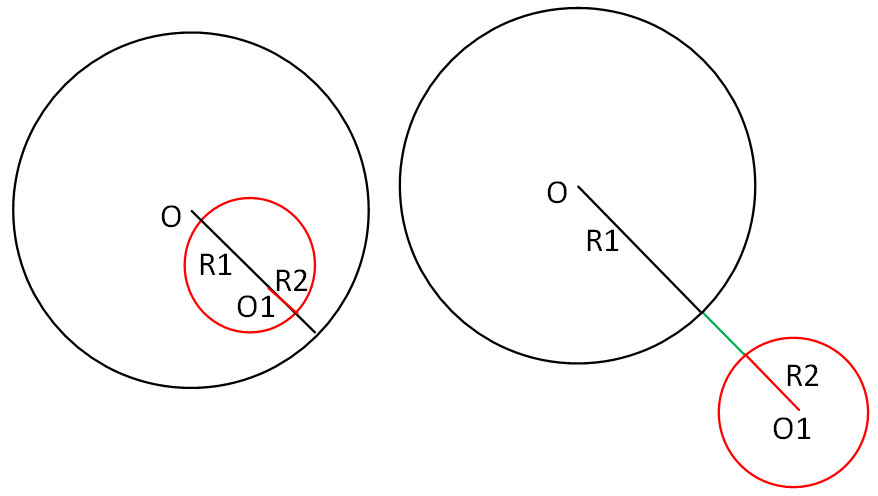
4. Ну и последний вариант, если ни один из выше перечисленных не подходит, тогда окружность пересекается в двух точках.
Полный текст решение задачи «Две окружности» с помощью Pascal будет иметь вид:
var r1,r2,x1,x2,y1,y2,r:real;
begin
assign (input,'input.txt'); reset (input);
assign (output,'output.txt'); rewrite (output);
read(input,x1,y1,r1,x2,y2,r2);
r:=sqrt(sqr(x2-x1)+sqr(y2-y1));
if (r1+r2>=r)and(r1+r>=r2)and(r2+r>=r1)
then write('YES')
else write('NO');
end.
Входные данные
Входной файл INPUT.TXT содержит в первой строке целые числа N, M, K (1<=N<=200, 1<=M<=200, 1<=K<=255). Далее следует N строк по M чисел в каждой — содержимое таблицы. Все числа в таблице целые, находятся в диапазоне от 0 до K включительно.
Выходные данные
 Выходной файл OUTPUT.TXT должен содержать K строк. Каждая строка должна описывать соответствующий ее номеру прямоугольник четырьмя числами X1 Y1 X2 Y2 (X1 и Y1 должны описывать координаты левого нижнего угла прямоугольника, а X2 и Y2 — координаты правого верхнего угла). Числа должны разделяться пробелом.
Выходной файл OUTPUT.TXT должен содержать K строк. Каждая строка должна описывать соответствующий ее номеру прямоугольник четырьмя числами X1 Y1 X2 Y2 (X1 и Y1 должны описывать координаты левого нижнего угла прямоугольника, а X2 и Y2 — координаты правого верхнего угла). Числа должны разделяться пробелом.
Начало координат расположено в левом нижнем углу таблицы. Таким образом, координаты левого нижнего угла поля — (0,0), правого верхнего — (M,N).
Пример
| № | INPUT.TXT | OUTPUT.TXT |
| 4 5 2 0 2 2 2 2 0 2 2 2 2 1 1 2 2 2 1 1 0 0 0 | 0 0 2 2 1 1 5 4 |
Решение:
var
xmin,xmax,ymin,ymax:array[1..255] of integer;
x,y,w,h,k,i,j:integer;
begin
assign(input,'input.txt'); reset(input);
assign(output,'output.txt'); rewrite(output);
read(h,w,k);
for i:=1 to k do
begin
xmin[i]:=w;
ymin[i]:=h;
end;
for y:=h downto 1 do
for x:=1 to w do
begin
read(j);
if j>0 then
begin
if x<xmin[j] then xmin[j]:=x;
if y<ymin[j] then ymin[j]:=y;
if x>xmax[j] then xmax[j]:=x;
if y>ymax[j] then ymax[j]:=y;
end;
end;
for i:=1 to k do writeln(xmin[i]-1,' ',ymin[i]-1,' ',xmax[i],' ',ymax[i]);
close(output);
end.
Var
max, min, x: longint;{ переменные для хранения максимального, минимального элемента и элемента массива.}
k,n,i: integer; {k – количество изменений элементов массива, n - количество элементов в массиве}
Begin
{особенности чтени/записи связаны с типами входных и выходных файлов}
assign(Input, 'Confuse.dat'); {связываем файл и файловую переменную. Такой способ (без объявления переменной Input) не работает в PascalABC}
reset(Input);// открываем файл для чтения
readln(n, k); // считываем n и k
max:=-2000000000; {считаем в качестве максимального минимальный элемент диапазона}
min:=2000000000;{считаем в качестве минимального максимальный элемент диапазона}
fori:=1 ton do {цикл для просмотра элементов массива}
Begin
read(x); // считываем i-ый элемент массива
ifx>Max thenMax:=x; {если найден элемент больший максимального – считаем его максимальным}
ifx<Min thenMin:=x; {если найден элемент меньший минимального – считаем его минимальным}
end;
assign(Output,'Confuse.sol');{связываем выходной файл и файловую переменную}
rewrite(Output);// открываем файл для записи
writeln(Max-Min); //выводим результат в файл
{закрываем открытые файлы}
close(input);
close(output);
end.
Пример входных и выходных данных
| lawn.in | lawn.out |
| 0 0 5 4 4 0 3 |
{Одно из возможных решений данной задачи заключается в следующем. Для каждой прямой, содержащей все пучки травы с равной координатой по оси абсцисс (аналогично можно рассматривать и ось ординат), найдем ее точки пересечения с окружностью, отображающей область действия поливальной установки, если, конечно, такие точки существуют. Получив данные точки, не сложно посчитать количество пучков травы на данной прямой одновременно и политых, и постриженных. Далее, просуммировав найденные числа для всех прямых, можно найти ответ на поставленную задачу.}
Var
x1,y1,x2,y2,x3,y3,x: longint;
k,r,y : longint;
input,output: text;
{функция определяет количество пучков травы, которые политы и подстрижены в исследуемом ряду}
functionkol(x,z1,z2:longint):longint;
Var
min,max,k: longint;
Begin
if(x<x1)or(x>x2)or(z1>y2)or(z2<y1) then{ряд не пересекает подстриженную область}
k:=0 {количество политых и подстриженных пучков равно 0}
else{иначе}
B
