Сечение поверхностей тел плоскостью. Развёртки
Вопросы для самоконтроля
1. Дайте определение многогранника. Какие многогранники называются правильными?
2. Какие многогранники называются пирамидой, призмой, призматоидом?
3. В каком случае призма называется прямой? В каком случае призма называется наклонной?
4. Какие правильные выпуклые многогранники называются взаимно соответствующими?
5. Как формулируется теорема Эйлера?
6. Чем задаются многогранники на комплексном чертеже? Как определяется видимость рёбер многогранника?
7. Что представляет собой сечение многогранника плоскостью? Каким способами можно решить задачу о пересечении многогранника плоскостью?
8. Как определить точки пересечения линии с поверхностью многогранника?
9. Что представляет собой линия пересечения двух многогранников?
10. Что называется развёрткой поверхности?
11. Какими свойствами обладают развёртки поверхностей?
12. Для каких поверхностей можно построить развёртки точные? Для каких поверхностей можно построить развёртки приближённые? Для каких поверхностей можно построить развёртки условные?
13. Как строятся развёртки приближённые?
14. Перечислите способы построения условных развёрток.
15. Как наносят на развёртку точку, принадлежащую поверхности?
1. Построить проекции линии пересечения поверхности тел проецирующей плоскостью (рис. 77)
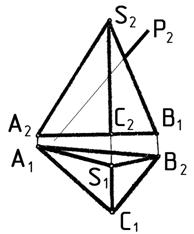
Рис. 30
2. Построить проекции и натуральную величину сечения призмы плоскостью S (DАВС) (рис. 31).
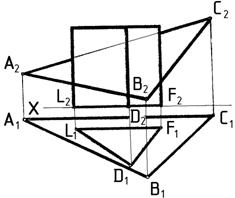
Рис. 31
3. Построить проекциилинии сечения поверхности тела плоскостью общего положения и определить натуральную величину сечения (рис.32 а, б).
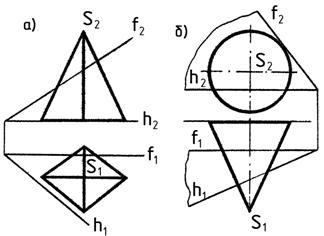
Рис. 32
Пересечение прямой линии с поверхностью
Вопросы для самоконтроля
1. Назовите способ нахождения точек пересечения линии с поверхностью и алгоритм решения задачи.
2. Какие посредники используются в случае пересечения с поверхностью кривой линии? Какие посредники используются в случае пересечения с поверхностью прямой линии?
3. В каком случае оправдано применение плоскостей общего положения в качестве посредников?
4. Назовите алгоритм решения задачи нахождения точки пересечения прямой общего положения с плоскостью общего положения.
1. Построить проекции точек пересечения прямой с поверхностью многогранника (рис.33).
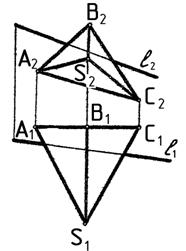
Рис. 33
2. Определить точки пересечения прямой с поверхностью цилиндра (рис.34).
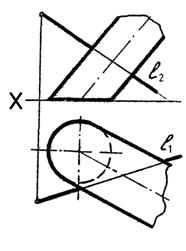
Рис. 34
3. Определить точки пересечения прямой с поверхностью тора (рис.35).
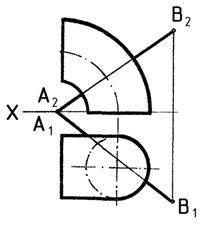
Рис. 35
Взаимное пересечение поверхностей
Вопросы для самоконтроля
1. В чём сущность метода вспомогательных секущих поверхностей?
2. Когда удобно применять способ вспомогательных секущих плоскостей?
3. В какой последовательности определяют линию пересечения поверхностей способом плоскостей?
4. Как выбирают положение вспомогательных секущих плоскостей?
5. По какому правилу определяется видимость точек линии пересечения поверхностей?
6. Какие точки линии пересечения называются особыми?
7. В чём особенность построения линии пересечения поверхностей, одна из которых проецирующая?
8. Какие поверхности вращения называются соосными?
9. По каким линиям пересекаются сфера и соосная с ней поверхность вращения?
10. На чём основан способ вспомогательных концентрических сфер?
11. Перечислите три условия, при выполнении которых можно применить способ концентрических сфер.
12. Как определяются сферы наибольшего и наименьшего радиусов при применении способа концентрических сфер?
13. По какому правилу определяется взаимопронизывание пересекающихся поверхностей при применении способа концентрических сфер?
14. Чем отличается способ эксцентрических сфер от способа концентрических сфер?
1. Построить проекции линии пересечения двух тел (рис.36 а,б).
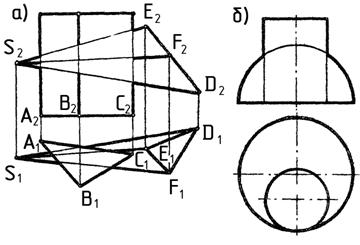
Рис. 36
2. Построить три проекции линии взаимного пересечения двух поверхностей (рис .37).
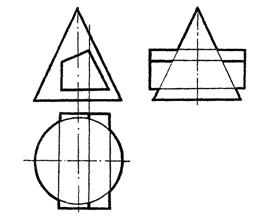
Рис. 37
3. Построить проекции линии пересечения двух тел (рис.38 а, б).
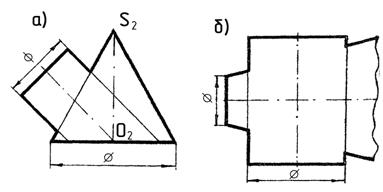
Рис. 38
ЛИТЕРАТУРА
Основная литература:
1. Нартова Л.Г. Начертательная геометрия: Учеб. - М.: Академия, 2011.
2. Гордон В.О. Начертательная геометрия. – М.: Высш. шк., 2002.
3. Гордон В.О. Сборник задач по курсу начертательной геометрии. – М.: Высш. шк., 2003.
Дополнительная литература:
1. Чекмарев А.А. Начертательная геометрия и черчение: Учеб. - М.: Юрайт, 2011.
2. Стрижаков А.В. и др. Начертательная геометрия: Учеб. пос. для вузов. - Ростов н/Д: Феникс, 2004.
СОДЕРЖАНИЕ
1. Методические указания к изучению курса
начертательная геометрия 2
2. Контрольная работа № 1 9
3. Контрольная работа № 2 14
4. Вопросы для самоконтроля и задачи, рекомендуемые
для подготовки к экзаменам 24
5. Литература 52
Таблица 1. Данные к задаче 1 (размеры и координаты, мм)
| № | ХА | УА | ZА | ХВ | УВ | ZВ | ХС | YС | ZС | ХD | YD | ZD | ХЕ | YЕ | ZЕ | ХК | YК | ZК |
Таблица 3. Данные к задаче 3(координаты и размеры, мм)
| № в | хА | yА | zА | хВ | yВ | zВ | хС | yС | zС | хD | yD | zD | хЕ | yЕ | zЕ | хК | yК | zК | хG | yG | zG | хU | yU | zU | h |
| 14i | |||||||||||||||||||||||||
| б | |||||||||||||||||||||||||
