Тема 1 Методы проецирования, терминология процесса проецирования

При выполнении технических чертежей применяют различные проекционные изображения. Любая техническая деталь представляет собой комплекс геометрических тел. Поэтому при составлении чертежа и его чтении необходимо уметь находить эти составляющие геометрические формы.

Различные способы изображения пространственных тел на плоскости, которые применяют при составлении чертежей и построении наглядных изображений основаны на методе проецирования, который заключается в том, что любая из множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность.

Для этого представим некоторую заданную плоскость Ки точку А в пространстве (рисунок 34).

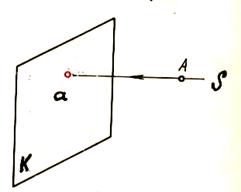Рисунок 34 – Заданная плоскость и точка в пространстве

Проводя из точки S луч через точку А в направлении плоскости К, мы получим точку а, в которой луч пересечёт её.

Познакомимся с терминологией проецирования:

- Принято точку в пространстве обозначать значком (.);

- Плоскость К, на которой получают проекцию, называется плоскостью проекции;

- (.)А в пространстве называется проецируемой точкой и обозначается прописными латинскими буквами А, В, С и т.д. ;

-Точка пересечения луча с плоскостью проекции К– а - называется проекцией точки и обозначается строчными буквами – а, б, с и т.д.;

- Прямая Аа (луч), с помощью которой находится проекция точки, называется проецирующим лучом.

Различные способы изображения пространственных форм на плоскости, которые применяют при составлении чертежей и построении наглядных изображений, основаны на методе проекций, включающем в себя два основных метода проецирования:

- параллельный (прямоугольный);

- центральный (косоугольный).

Рассмотрим параллельный метод проецирования,который заключается в переносе точек при помощи параллельных лучей (рисунок 35).

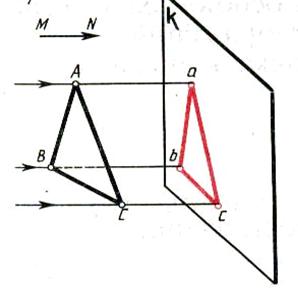Рисунок 35 – Параллельный метод проецирования

Возьмём в пространстве прямоугольник АВС, направление проецирующего луча MN и плоскость проекции К.

Через точки треугольника А, В, С проводим прямые Аа, Вв, Сс параллельные проецирующему лучу MN до пересечения с плоскостью проекций К, получаем проекции точек а, б, в. Соединив проекции точек, получим проекцию треугольника АВСв пространстве на плоскости проекций - авс.

Изображение треугольника авс на плоскости проекций К, построенное с помощью параллельных проецирующих лучей называется параллельной проекцией.

Проекция называется прямоугольной, если проецирующие лучи перпендикулярны плоскости проекций, и косоугольной, если они не перпендикулярны ей.

При параллельном проецировании размеры предмета не искажаются, поэтому широко применяется в техническом черчении.

Центральный метод проецированияполучают, если проецирующие лучи проходят через заданную точку – центр проецирования (рисунок 36).

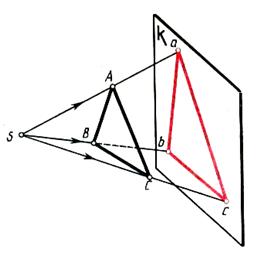Рисунок 36 – Центральный метод проецирования

Треугольник АВС в пространстве, плоскость проекций К, заданная точка в пространстве S– центр проецирования. Из центра проецирования S проводим проецирующие лучи через точки А, В, С до пересечения с плоскостью проекций К, получаем точки проекций а, в, с на плоскости проекций. Соединив точки а, в,с, получим проекцию треугольника авс на плоскости проекций Ктреугольника АВСв пространстве.

Изображение, построенное с помощью проецирующих лучей, проведённых из центра проецирования через точки в пространстве, называется центральной проекцией.

Примером центральных проекций являются фотоснимки, изображения на экране, так как центром проецирования является оптический центр объектива фото- или киноаппарата.

Материал для закрепления:

1. Показать значок изображения точки в пространстве.

2. Дать определения:

а) точки в пространстве;

б) плоскости, на которой получают проекцию;

в) прямая, с помощью которой определяют проекцию точки;

г) точки пересечения проецирующего луча с плоскостью проекций;

д) точки, из которой выходят проецирующие лучи.

3 Назвать методы проецирования.

4 Объяснить получение параллельного метода проецирования.

5 Объяснить получение центрального метода проецирования.