Результат 3 Выполнять геометрические построения

Входной тест:

· Дать определение «чертёж».

· Назвать масштабы для выполнения чертежей.

· Назвать линии для выполнения чертежа.

· Объяснить назначение шрифта.

· Указать назначение формата, дать его определение.

· Объяснить назначение размерных линий.

Изучение учебного материала результата позволит обучающемуся:

· Получить навыки графических приёмов деления;

· Получить навыки выполнения сопряжений;

· Выполнять нанесение размерных линий и размеров в соответствии со стандартом;

· Применять типы линий в соответствии с назначением.

Прочитать учебный материал, зафиксировать его в конспекте, подготовиться к закреплению и выполнению графического задания.

Тема 1 Графические приёмы деления отрезков, углов, окружностей

При выполнении чертежей приходится производить различные геометрические построения. С некоторыми из них мы познакомимся.

Деление отрезка пополам (на две равные части)

Из концов отрезка АВпроводим дуги окружности, радиус которой больше половины отрезка. Прямая, соединяющая точки пересечения дуг, разделит отрезок на две равные части (рисунок 18).

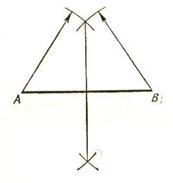Рисунок 18 – Деление отрезка пополам

Деление отрезка на любое число равных частей

Из точки А отрезка АВ под любым углом проводим вспомогательную прямую. На этой прямой от точки А откладываем последовательно равные отрезки любой длины, число которых равно числу делений отрезка АВ (например – 7 частей). Полученную точку 7соединяем с точкой В отрезка АВ и через точки делений 1, 2, 3, 4, 5, 6 проводим прямые, параллельные отрезку 7В. Пересекаясь с отрезком АВ, эти прямые разделят отрезок на 7 равных частей. Для проверки возьмите раствором циркуля отрезок А1 и отложите его по прямой АВ, вы убедитесь, что отрезки А1, 12, 23, 34, 45, 56, 67 равны (рисунок 19).

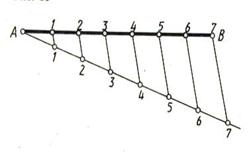Рисунок 19 – Деление отрезка на равные части

Деление угла пополам

Из вершины В угла АВС проводим произвольным радиусом дугу, которая пересечёт стороны угла в точках Е и Д. Из этих точек делаем засечки дугой, радиус которой больше половины отрезка ДЕ, получаем точку F. Биссектриса угла ВFразделит угол АВС пополам (рисунок 20а). Так можно разделить угол на 4, 8, 16 равных частей.

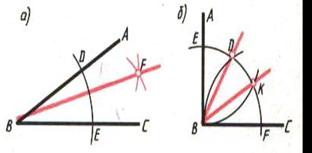а – деление угла пополам; б – деление прямого угла на три равные части   Рисунок 20 – Деление угла

Деление прямого угла на три равные части

Из точки вершины В прямого угла АВС проводим произвольным радиусом дугу, которая пересечёт стороны угла в точках Е и F. Из этих точек тем же радиусом делаем засечки на проведённой дуге, получаем точки Д и К. Через полученные точки проводим прямые ВДи ВК, делящие прямой угол на три равные части (рисунок 20б).

Деление окружности на равные части. Построение правильных многоугольников

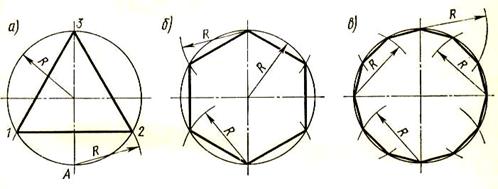
На 3, 6, 12 равных частей

Для деления окружности на 3 равные части, необходимо построить окружность заданного радиуса. Для этого сначала проводим центровые линии тонкой штрихпунктирной линией, на пересечении которых получаем центр окружности точку О (на пересечении штрихов линии). Из нижней точки А пересечения вертикальной центровой линии с окружностью сделать засечки радиусом окружности R в обе стороны от точки на окружности, получим точки 1 и 2. Точка 3находится на пересечении диаметра окружности в верхней части её (напротив точки А). Соединив точки 1, 2и3отрезками прямой, получим вписанный в окружность равносторонний треугольник (рисунок 21а). Для проверки возьмите раствором циркуля сторону 1-2 и отложите её по остальным двум сторонам треугольника.