Улучшение качества изображения фильтрацией

А.И. Дружинин, В.В. Вихман

Алгоритмы компьютерной графики: Учеб. пособие. – Новосибирск: Изд-во НГТУ, 2003. – с.

В учебном пособии рассмотрены основополагающие алгоритмы, используемые в компьютерной графике: построение отрезков и окружностей, фильтрации, построчного заполнения и заливки с затравочной точкой многоугольников, отсечения отрезков и многоугольников. Пособие состоит из теоретического описания алгоритмов и заданий к лабораторным работам и является руководством к выполнению их студентами, а также к написанию программ более высокого уровня.

Пособие адресовано студентам младших курсов и преподавателям смежных дисциплин. Оно может быть полезно разработчикам программного обеспечения. Предполагается в ближайшее время написание второй части учебного пособия с описанием алгоритмов трехмерной графики.

Авторы работы выражают особую благодарность инженерам кафедры вычислительной техники О.В. Малявко и А.Р. Исаеву А.Р. за оформление учебного пособия.

	©

Новосибирский государственный технический университет, 2003.

1. Генерация векторов

Цель: Изучить алгоритмы разложения отрезка в растр:
алгоритм цифрового дифференциального анализатора (ЦДА), алгоритм Брезенхема. Сравнить результаты применения
алгоритмов между собой

Назначение генератора векторов – соединение двух точек изображения отрезком прямой. Далее будут рассмотрены следующие алгоритмы:

· алгоритм ЦДА – цифрового дифференциального анализатора (DDA – Digital Differential Analyser) для генерации векторов – симметричный и несимметричный;

· алгоритм Брезенхема для генерации векторов.

Перед рассмотрением конкретных алгоритмов сформулируем общие требования к изображению отрезка:

· концы отрезка должны находиться в заданных точках;

· отрезки должны выглядеть прямыми;

· яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона;

· построение должно быть быстрое.

Ни одно из этих условий не может быть точно выполнено на растровом дисплее в силу того, что изображение строится из пикселов конечных размеров, а именно:

· концы отрезка в общем случае располагаются на пикселах, лишь наиболее близких к требуемым позициям и только в частных случаях координаты концов отрезка точно совпадают с координатами пикселов;

· отрезок аппроксимируется набором пикселов и лишь в частных случаях вертикальных, горизонтальных и отрезков под 45° они будут выглядеть прямыми, причем гладкими прямыми, без ступенек только для вертикальных и горизонтальных отрезков (рис. 1.1);

· яркость для различных отрезков и даже вдоль отрезка в общем случае различна, так как, например, расстояние между центрами пикселов для вертикального отрезка и отрезка под углом 45° различно (рис. 1.1).

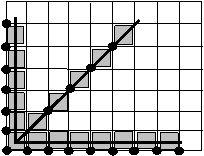Рис. 1.1. Растровое представление различных векторов

Цифровой дифференциальный анализатор (ЦДА)

С помощью алгоритма ЦДА решается дифференциальное уравнение отрезка, имеющее вид:

,

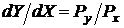где 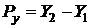– приращение координат отрезка по оси Y; 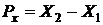– приращение координат отрезка по оси X; X₂, Y₂, X₁,Y₁ – начальная и конечная координаты отрезка.

При этом ЦДА формирует дискретную аппроксимацию непрерывного решения этого дифференциального уравнения. В симметричном ЦДА тем или иным образом определяется количество узлов N, используемых для аппроксимации отрезка. Затем за N циклов вычисляются координаты очередных узлов:

,

.

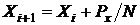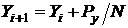Получаемые значения 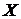и 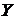преобразуются в целочисленные значения координаты очередного подсвечиваемого пиксела. Генератор векторов, использующий этот алгоритм, имеет тот недостаток, что точки могут прописываться неоднократно, что увеличивает время построения, или отрезок будет выглядеть прерывистым.

Кроме того, из-за независимого вычисления обеих координат нет предпочтительных направлений и построенные отрезки кажутся не очень красивыми. Субъективно лучше смотрятся вектора с единичным шагом по большей относительной координате (несимметричный ЦДА). Для 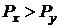(при 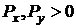) это означает, что координата по X направлению должна увеличиться на 1 P_x раз, а координата по Y направлению должна также P_x раз увеличиться, но на 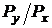, т.е. количество узлов аппроксимации берется равным числу пикселов вдоль наибольшего приращения. Для генерации отрезка из точки (X₁,Y₁) в точку (X₂,Y₂) в первом октанте алгоритм несимметричного ЦДА имеет вид:

x – integer;

Вычислить приращения координат:
;
;

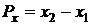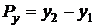Занести начальную точку отрезка
PutPixel (x₁,y₁);

Сгенерировать отрезок
while (x₁ < x₂) {
x₁:= x₁ + 1;
y₁:= y₁ + P_y/P_x;
PutPixel (intl (x₁), intl (y₁));
}

Примечание: intl – приближение к нижнему, т.е. 5.3 = 5; 5.6 = 5; –5.3 = –6; –5.6 = –6.

Пример генерации отрезка по алгоритму несимметричного ЦДА приведен на рис. 1.2.

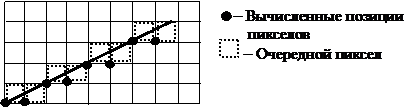Рис. 1.2. Генерация отрезка несимметричным ЦДА

Генерация отрезка:

if (abs (x₂ – x₁) >= abs (y₂ – y₁)) then

len:= abs (x₂ – x₁) else

len:= abs (y₂ – y1);

;
;

;

;

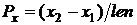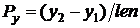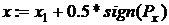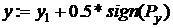i = 1

while (i <= len) {
PutPixel (intl (x), intl (y));
x:= x + P_x;
y:= y+P_y;
i:= i + 1

}

Алгоритм Брезенхема

Так как приращения координат, как правило, не являются целой степенью двойки, то в ЦДА – алгоритме (см. предыдущий пункт) требуется выполнение деления, что не всегда желательно. Алгоритм выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат – либо X, либо Y (в зависимости от углового коэффициента) – изменяется на единицу, изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние назовем ошибкой.

Брезенхем предложил алгоритм, построенный так, что требуется проверять лишь знак этой ошибки. На рис. 1.3,а,б это иллюстрируется для отрезка в первом октанте, т.е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0,0) больше чем 1/2, то его пересечение с прямой 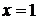будет расположено ближе к прямой 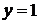, чем к прямой 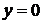. Следовательно, точка растра (1,1) лучше аппроксимирует ход отрезка, чем точка (1,0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента, равного 1/2 нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1,1). Не все отрезки проходят через точки растра (рис. 1.3 в). Здесь отрезок с тангенсом угла наклона 3/8 сначала проходит через точку растра (0,0) и последовательно пересекает три пиксела. Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной – 1/2.

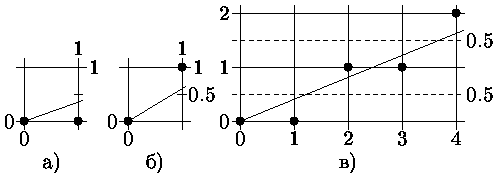
Рис. 1.3. Алгоритм Брезенхема генерации отрезков

Если Е < 0 (где Е – ошибка), то Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.

Для вычисления Е положим, что рассматриваемый вектор начинается в точке (0,0) и проходит через точку (4, 1.6) (рис. 1.3,в), т.е. имеет положительный наклон, меньший 1.

Из рис. 1.3,в) видно отклонение для первого шага:

,

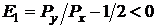поэтому для занесения пиксела выбирается точка (1,0).

Отклонение для второго шага вычисляется добавлением приращения Y-координаты для следующей X-позиции (рис. 1.3 в):

,

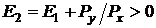поэтому для занесения пиксела выбирается точка (2,1). Так как отклонение считается от Y-координаты, которая теперь увеличилась на 1, то из накопленного отклонения для вычисления последующих отклонений надо вычесть 1:

E₂ = E₂ – 1.

Отклонение для третьего шага:

,

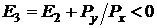поэтому для занесения пиксела выбирается точка (3,1).

Возможны случаи:

E1 > 0	E1 <= 0
ближайшая точка есть:
X1 = X0 + 1; Y1 = Y0+1,	X1 = X0 + 1; Y1 = Y0,
E2 = E1 + Py/Px – 1;	E2 = E1 + Py/Px.

Так как интересует только знак Е, то можно избавиться от деления умножением E на 2*Px:

	E1 = 2* Py – Px ,
E1 > 0,	E2 = E1 + 2 (Py – Px),
E1 <= 0;	E2 = E1 + 2* Py.

Таким образом, получается алгоритм, в котором используются только целые числа, сложение (умножение на 2 – сдвиг влево или сложение с самим числом):

X = x₁;
Y = y₁;
P_x = x₂ – x₁;
P_y = y₂ – y₁;
E = 2*P_y – P_x;
i = P_x;
PutPixel(X, Y); /* Первая точка вектора */
while (i= i – 1³ 0){
if (E 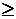0){
X= X + 1;
Y= Y + 1;
E= E + 2*(P_y – P_x);
} else
X= X + 1;
E= E + 2*P_y;
PutPixel(X, Y); /* Очередная точка вектора */
}

Этот алгоритм пригоден для случая 0 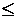dY 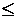dX. Для других случаев алгоритм строится аналогичным образом.

На рис. 1.4 приведен пример генерации по алгоритму Брезенхема того же самого отрезка, что и показанного на рис. 1.2 для генерации по алгоритму несимметричного ЦДА.

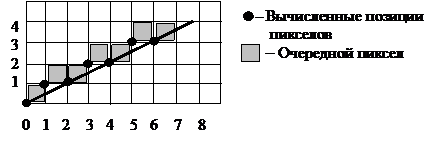Рис. 1.4. Генерация отрезка по алгоритму Брезенхема

Задание на лабораторную работу № 1
"Генерация векторов"

1. Центр отрезка находится в середине экрана.

1.1. Разложить в растр отрезок по методу цифрового дифференциального анализатора (ЦДА) с произвольными координатами.

1.2. Разложить в растр отрезок, используя алгоритм Брезенхема с произвольными координатами.

2. Используя разные цвета, разложите в растр отрезок на одной системе координат с помощью метода ЦДА и Брезенхема. Сравните полученные результаты. Сделайте выводы.

3. Нарисуйте "настоящий" отрезок и сравните результаты работы алгоритмов.

4. Сравните алгоритмы ЦДА и Брезенхема. Приведите примеры их сходства и различия.

2. Фильтрация.
Модифицированный алгоритм Брезенхема

Цель: Изучить алгоритмы фильтрации: модифицированный
алгоритм Брезенхема и масочную фильтрацию

2.1. Модифицированный алгоритм Брезенхема

Основная идея алгоритма состоит в том, что для ребер многоугольника устанавливается яркость пиксела пропорционально площади пиксела, попавшей внутрь многоугольника. На рис. 2.1 приведена иллюстрация построения ребра многоугольника с тангенсом угла наклона 11/21.

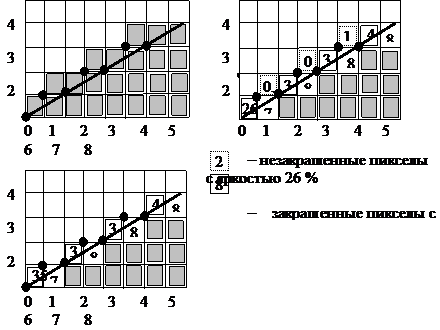Рис. 2.1. Устранение ступенчатости ребер многоугольника:

а – генерация ребер без устранения ступенчатости;

б – точное вычисление интенсивности пикселов границы;

в – формирование пикселов границы по модифицированному методу Брезенхема

На рис. 2.1,а показан результат генерации многоугольника с использованием ранее рассмотренного алгоритма Брезенхема при двухуровневом изображении (пиксел или закрашен или не закрашен). На рис. 2.1,б показан результат генерации многоугольника с вычислением интенсивности пикселов, через которые проходит ребро многоугольника. Интенсивность вычисляется пропорционально площади части пиксела, попавшей внутрь многоугольника. На рис. 2.1,в показан результат генерации многоугольника с вычислением интенсивности пиксела, через который проходит ребро многоугольника в соответствии с модифицированным алгоритмом Брезенхема. Суммарная площадь частей для двух пикселов, попавшая внутрь многоугольника, равна (dy + t)/ 2, где t – тангенс угла наклона (рис. 2.2). Если теперь в исходном алгоритме Брезенхема заменить отклонение E на E' = E + (1 – t), то 0 £ E' £ 1) и значение E' будет давать значение той части площади пиксела, которая находится внутри многоугольника.

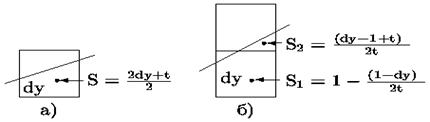
Рис. 2.2. Устранение ступенчатости за счет учета площади
пикселов, пересекаемых ребром многоугольника

Выполняя преобразование над значением отклонения для первого шага (рис. 2.1), получим, что начальное значение станет равным 1/2.

Максимальное значение отклонения 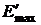, при превышении которого производится увеличение Y-координаты занесения пикселов, станет равным
(1 – t).

Для того чтобы оперировать не дробной частью максимальной интенсивности, а непосредственно ее значениями достаточно домножить на полное число уровней интенсивности I тангенс угла наклона (t), начальное ( 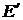) и максимальное ( 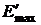) значения отклонения.

В результате получается следующий алгоритм, пригодный для случая
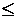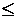0 dY dX:

X = x₁;
Y = y₁;
P_x = x₂ – x₁;
P_y = y₂ – y₁;
t = I*P_y / P_x;
E' = I / 2;

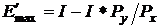
i = P_x;
PutPixel(X, Y, t/2); /* Первая точка вектора */
while (i = i – 1 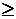0){
if ( ){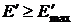
X= X + 1;
Y= Y + 1;

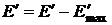
} else
X = X + 1;
E' = E' + t;
PutPixel(X, Y, E'); /* Очередная точка вектора */
}

Для избавления от вещественной арифметики при манипулировании с 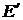можно помножить уже упомянутые величины на 2*P_x.

Заливка области с затравкой

Цель: Изучить алгоритмы заливки области с затравкой.
Понять, в чем основное отличие заливки области
от заполнения многоугольника

5.1. Заливка области с затравкой

По способу задания области делятся на два типа (рис. 5.1):

· гранично-определенные, задаваемые своей (замкнутой) границей такой, что коды пикселов, границы которых отличны от кодов внутренней, перекрашиваемой части области. На коды пикселов внутренней части области налагаются два условия – они должны быть отличны от кода пикселов границы и кода пиксела перекраски. Если внутри гранично-определенной области имеется еще одна граница, нарисованная пикселами с тем же кодом, что и внешняя граница, то соответствующая часть области не должна перекрашиваться;

· внутренне-определенные, нарисованные одним определенным кодом пиксела. При заливке этот код заменяется на новый код закраски.

а

б

Рис. 5.1. Деление области по способу задания:

а – внутренне-определенная область;

б – гранично-определенная область

Основное отличие заливки области с затравкой от заполнения многоугольника: в последнем случае мы сразу имеем всю информацию о предельных размерах части экрана, занятой многоугольником. Поэтому определение принадлежности пиксела многоугольнику базируется на быстро работающих алгоритмах, использующих когерентность строк и ребер (см. предыдущий раздел). В алгоритмах же заливки области с затравкой нам вначале надо прочитать пиксел, затем определить, принадлежит ли он области и, если принадлежит, то перекрасить.

Заливаемая область или ее граница – некоторое связное множество пикселов. По способам доступа к соседним пикселам области делятся на 4- и 8-связные. В четырех связных областях доступ к соседним пикселам осуществляется по четырем направлениям – горизонтально влево и вправо и вертикально – вверх и вниз. В 8-связных областях к этим направлениям добавляются еще 4 диагональных. Используя связность, мы можем, двигаясь от точки затравки, достичь и закрасить все пикселы области.

Важно отметить, что для 4-связной прямоугольной области граница 8-связна (рис. 5.2,а) и, наоборот, у 8-связной области граница 4-связна (рис. 5.2,б). Поэтому заполнение 4-связной области 8-связным алгоритмом может привести к "просачиванию" через границу и заливке пикселов в примыкающей области.

а б

Рис. 5.2. Связанность областей:

а – 4-связные; б – 8-связные, внутренне-определенные области

В общем, 4-связную область мы можем заполнить как 4-, так и 8-связным алгоритмом. Обратное же неверно.

С использованием связности областей и стека можно построить простые алгоритмы закраски как внутренне, так и гранично-определенной области.

Простой алгоритм заливки

Рассмотрим простой алгоритм заливки гранично-определенной 4-связной области. Заливка выполняется следующим образом:

· определяется, является ли пиксел граничным или уже закрашенным;

· если нет, то пиксел перекрашивается, затем проверяются и, если надо, перекрашиваются 4 соседних пиксела.

Ниже приведен итеративный алгоритм закраски 4-связной гранично-определенной области. Логика работы алгоритма следующая:

· поместить координаты затравки в стек;

· пока стек не пуст;

· извлечь координаты пиксела из стека;

· перекрасить пиксел;

· для всех четырех соседних пикселов проверить, является ли он граничным или уже перекрашен.

· если нет, то занести его координаты в стек.

На рис. 5.3,а а показан выбранный порядок перебора соседних пикселов, а на рис. 5.3,б – соответствующий ему порядок закраски простой гранично-определенной области.

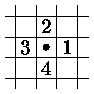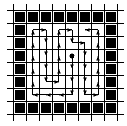Рис. 5.3. Заливка 4-х связной области итеративным алгоритмом:

a – порядок перебора соседних пикселов;

б – порядок заливки области

Рассмотренный алгоритм легко модифицировать для работы с 8-ми связными гранично-определенными областями или же для работы с внутренне-определенными.

Как уже отмечалось, очевидный недостаток алгоритмов, непосредственно использующих связность закрашиваемой области, – большие затраты памяти на стек, так как на каждый закрашенный пиксел в стеке по максимуму будет занесена информация о еще трех соседних. Кроме того, информация о некоторых пикселах может записываться в стек многократно. Это приведет не только к перерасходу памяти, но и потере быстродействия за счет многократной раскраски одного и того же пиксела.

Двумерный FC-алгоритм

В данном алгоритме кодируется весь отрезок целиком. Схема кодирования близка к используемой в алгоритме Коэна-Сазерленда. Все пространство экрана разбивается на 9 частей и они кодируются цифрами от 1 до 9 (рис. 6.2). Отрезок кодируется следующим образом:

LineCode(V₀V₁) = Code(V₀)*16 + Code(V₁),

где Code(V₁) – код конечной точки;

Code(V₀) – код начальной точки,

*16 – означает сдвиг влево на 4 разряда,

LineCode(V₀V₁) – код отрезка.

Рис. 6.2. Задние кодов областей для FC-алгоритма

Так как каждый код может принимать только девять значений, то имеется 81 возможный вариант расположения отрезка и требуется свой набор вычислений для определения отсечения отрезка за минимальное время. Однако, имеется всего 8 основных случаев отсечения, остальные симметричны им. Иллюстрации для случаев 1-7 приведены на рис. 6.3, а для случая 8 – на рис. 6.4. Итак:

Случай 1 – начальная и конечная точки отрезка находятся в области 4 (отрезок LA, LineCode(V₀V₁) = 44). Отрезок не пересекает видимую область и отбрасывается.

Случай 2 – начальная точка находится в области 4, конечная – в области 1 (отрезок LB, LineCode(V₀V₁) = 41). Отрезок не пересекает видимую область и отбрасывается.

Случай 3 – начальная точка находится в области 4, конечная – в области 2 (отрезки LC и LD, LineCode(V₀V₁) = 42). Отрезок явно пересекает X_лев. Вычисляем точку пересечения отрезка с левым ребром – (X_лев, Y_п). Eсли Y_п > Y_верхн, то

Рис. 6.3 Варианты расположения отрезка для
неугловых областей (FC-алгоритм)

Рис. 6.4. Варианты расположения отрезка для
угловых областей (FC-алгоритм)

это отрезок LC, он не пересекает видимую область и отбрасывается. Иначе, это отрезок LD, пересекающий видимую область и необходимо вычислить точку пересечения отрезка с Y_верхн и изобразить видимую часть отрезка.

Случай 4 – начальная точка находится в области 4, конечная – в области 3 (отрезки LE, LF и LG, LineCode(V₀V₁) = 43). Вычисляем точку пересечения с левым ребром – (X_лев, Y_п1). Eсли Y_п1 > Y_верхн, то это отрезок LE, он не пересекает видимую область и отбрасывается, иначе это отрезки LF или LG. Вычисляем точку пересечения с правым ребром (X_прав, Y_п2). Eсли Y_п2 > Y_верхн, то это отрезок LF и необходимо вычислить точку пересечения с верхним ребром и изобразить видимую часть отрезка. Иначе это отрезок LG, точки пересечения с левым и правым ребрами известны, следовательно, изображаем видимую часть отрезка.

Случай 5 – начальная точка находится в области 4, конечная – в области 6 (отрезок LH, LineCode(V₀V₁) = 46). Вычисляем точки пересечения с левым и правым ребрами и изображаем видимую часть отрезка.

Случай 6 – начальная точка находится в области 4, конечная – в области 5 (отрезок LI, LineCode(V₀V₁) = 45). Вычисляем точку пересечения с левым ребром и изображаем видимую часть отрезка.

Случай 7 – начальная точка находится в области 5, конечная – в области 5 (отрезок JK, LineCode(V₀V₁) = 55). Отрезок полностью видим, изображаем его.

Случай 8 – начальная точка находится в области 7, конечная – в области 3 (отрезки RW, SX, SY, TX,TY,UZ LineCode(V₀V₁) = 73). Вычисляем точку пересечения с левым ребром – (X_лев, Y_п1). Eсли Y_п1 > Y_верхн, то это отрезок RW, он не пересекает видимую область и отбрасывается. Вычисляем точку пересечения с правым ребром ребром – (X_прав, Y_п2). Eсли Y_п2 < Y_нижн, то это отрезок UZ, он не пересекает видимую область и отбрасывается. Если Y_п1 > Y_нижн, то начальная точка S и если Y_п2 < Y_вехн, то это отрезок SY и мы изображаем его видимую часть, иначе, это отрезок SX, вычисляем точку пересечения с верхней стороной и также изображаем видимую часть отрезка. Оставшийся вариант – начальная точка T и если Y_п2 < Y_вехн, то это отрезок TY и мы изображаем его видимую часть, иначе, это отрезок TX, вычисляем точку пересечения с верхней стороной и также изображаем видимую часть отрезка.

Алгоритм Кируса-Бека

Алгоритм Кируса-Бека относится к классу алгоритмов с параметрическим представлением отрезка и окна отсечения. При создании надежного алгоритма отсечения необходимо иметь хороший метод определения местоположения относительно окна точки, принадлежащей отрезку, – внутри, на границе или вне окна. Для этого в алгоритме Кируса-Бека используется вектор нормали.

Возьмем выпуклую двумерную область R (рис. 6.5) – она должна быть выпуклым многоугольником. Внутренняя нормаль в точке a, лежащей на границе R, удовлетворяет условию:

n_вн*(b– a) ³ 0,

где b – любая точка, лежащая на границе R.

Рис. 6.5. Определение местоположения точки относительно
окна отсечения в алгоритме Кируса-Бека

Так как скалярное произведение двух векторов равно:

V₁*V₂ = çV₁ç*çV₂ç*cos(Q),

где Q - меньший из двух углов, образованных V₁ и V₂. Причем, если Q = p/2, то V₁*V₂ = 0 и вектора V₁и V₂ перпендикулярны. Угол Q между n_вн и любым вектором между точками a и b всегда принадлежит интервалу –p/2 £ Q£ p/2 и, следовательно, cos(Q) всегда ³ 0 и скалярное произведение n_вн*(b – a) неотрицательно (для внешней (наружной) нормали скалярное произведение n_нар*(b – a) всегда неположительно).

Параметрическое представление отрезка имеет вид:

P(t) = P₁ + (P₂ – P₁)*t; 0 £ t £ 1.

Если f – граничная точка выпуклой области R, а n – внутренняя нормаль к одной из ограничивающих эту область плоскостей, то для любой конкретной величины t (т.е. для любой точки отрезка P₁P₂) из условия n*(P(t) – f) < 0 следует, что вектор (P(t) – f) направлен вовне области R, из условия n*(P(t) – f) = 0 следует, что вектор (P(t) – f) принадлежит плоскости, которая проходит через f, и перпендикулярен нормали, из условия n*(P(t) – f) > 0 следует, что вектор
(P(t) – f) направлен внутрь области R (рис. 6.6).

Из всех условий взятых вместе следует, что бесконечная прямая пересекает замкнутую область (выпуклую двумерную) ровно в двух точках и уравнение n*(P(t) – f) = 0 имеет только одно решение и точка P(t) будет точкой пересечения отрезка с граничной плоскостью.

Из всего вышесказанного и вытекает алгоритм Кируса-Бека.

Параметрическое описание отрезка (как уже отмечалось выше) имеет вид:

P(t) = P₁ + (P₂ – P₁)*t; 0 £ t £ 1.

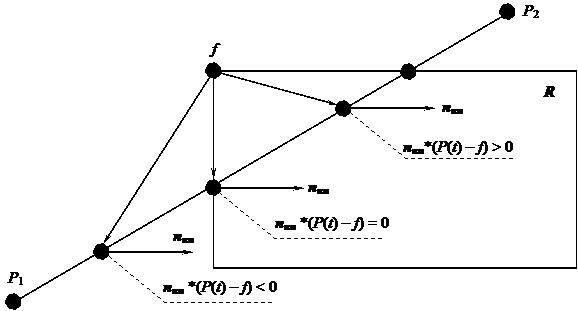
Рис. 6.6. Исходные данные для алгоритма Кируса-Бека

Скалярное произведение внутренней нормали на вектор, начинающийся в произвольной точке отрезка и заканчивающийся в другой точке, лежащей на той же границе окна (n_i*(P(t) – f_i ); i = 1,2…) будет положительным, равным нулю или отрицательным в зависимости от того, будет ли избранная точка отрезка лежать с внутренней стороны границы, на самой границе или с ее внешней стороны. Это справедливо для любого ребра. Подставим P(t) для нахождения пересечения:

n_i*[P₁ + (P₂ – P₁)*t – f_i] = 0

Или в другой форме:

n_i*[P₁ –f_i] +n_i*[P₂ – P₁]*t = 0

Вектор (P₂ – P₁) – определяет ориентацию отрезка, а вектор (P₁ – f_i) пропорционален расстоянию от первого конца отрезка до избранной граничной точки. Обозначим D = (P₂ – P₁) – директриса или ориентация отрезка, а
w_i = (P₁ – f_i) – весовой множитель, тогда:

t*(n_i*D) + w_i*n_i = 0
t = –(w_i*n_i) / (n_i*D); D ¹ 0; i = 1, 2, 3, …

Равенство D нулю означает, что P₂ = P₁, т.е. вырождение отрезка в точку и при этом если w_i*n_i < 0, то точка вне окна отсечения, если w_i*n_i = 0, то точка находится на границе окна отсечения, если w_i*n_i > 0, то точка внутри окна отсечения. Вычисляем t, если значение лежит за пределами интервала 0 £ t £ 1, то можно его проигнорировать. Может получиться более двух значений t в допустимом интервале. Эти значения следует разбить на две группы: нижнюю и верхнюю в зависимости от того, к началу или к концу отрезка будет ближе вычисленная точка. Необходимо найти наибольшую из нижней группы и наименьшую из верхней группы. При этом если n_i*D > 0, то найденное значение t рассматривается в качестве возможного нижнего предела, иначе – верхнего. Блок – схема алгоритма приведена на рис. 6.7.

Рис. 6.7. Алгоритм Кируса-Бека

Для успешной реализации алгоритма Кируса-Бека необходимо знать, выпуклый многоугольник или нет, и определить уравнение внутренней нормали.

Заключение

В данном учебном пособии были рассмотрены основные алгоритмы компьютерной графики, без которых было бы невозможно написание таких программ как WinWord, CorelDraw и Acrobat Reader.

Список используемой литературы очень обширен, а конкретная реализация алгоритма зависит только от квалификации программиста, но приведем основные источники, которыми пользовались авторы при написании данного пособия:

- Роджерс Д. Алгоритмические основы машинной графики: Пер. с англ.: М.: Мир, 1989.

- Вельтмандер П.В. Алгоритмы компьютерной графики: http://ermak.cs.nstu.ru/kg_rivs

- D. Hearn, P. Baker, Computer Graphics: Prentice Hall, Inc., Englewood Cliffs, New Jersey, 1994.

оглавление

Стр.

1. Генерация векторов........................................................................................ 3

1.1. Цифровой дифференциальный анализатор (ЦДА).................................. 4

1.2. Алгоритм Брезенхема............................................................................... 5

Задание на лабораторную работу № 1 "Генерация векторов"...................... 8

2. Фильтрация. Модифицированный алгоритм Брезенхема........................... 9

2.1. Модифицированный алгоритм Брезенхема............................................. 9

2.2. Улучшение качества изображения фильтрацией................................... 11

Задание на лабораторную работу № 2 "Фильтрация. Модифицированный алгоритм Брезенхема "................................................................................................... 12

3. Алгоритмы генерации окружности.............................................................. 13

3.1. Целочисленный алгоритм Брезенхема................................................... 13

3.2. Алгоритм Мичнера для построения окружности.................................. 17

Задание на лабораторную работу № 3 "Алгоритмы генерации окружности"..... 17

4. Алгоритмы построчного заполнения многоугольников............................ 18

Задание на лабораторную работу № 4 "Алгоритмы построчного

заполнения многоугольников"...................................................................... 20

5. Заливка области с затравкой........................................................................ 22

5.1. Заливка области с затравкой.................................................................. 22

5.2. Простой алгоритм заливки..................................................................... 23

5.3 Построчный алгоритм заливки с затравкой........................................... 24

Задание на лабораторную работу № 5 "Заливка области с затравк