Трехмерное моделирование многогранников

Правильные многогранники – это геометрические фигуры, состоящие из конечного числа плоских правильных многоугольников (см. рис. 76);

Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности.

Рис. 76

Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью.Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками.

Стороны граней называются ребрами многогранника, а вершины — вершинами многогранника

УПРАЖНЕНИЕ 1.Построить трехмерную модель куба.

Построение 3-х мерной модели куба аналогично построению 3-х мерной модели параллелепипеда (см. лаб. раб. №6), кроме задания параметров сторон куба.

Алгоритм построения модели куба

1. Запустите программу Компас 3D LT (ПускaПрограммыaКомпас3D LT 5.11aярлык Компас3D LT 5.11).

2. Для построения трехмерной модели геометрических объектов щелкните ЛКМ на кнопке Новая деталь , находящейся в Панели управления КОМПАС 3D LT.

3. В Дереве построений КОМПАС 3D LT нажатием ЛКМ выберите Фронтальную плоскость, в которой будет производиться построение эскиза вида спереди куба.

4. В Панели управления системы Компас нажатием кнопки Новый эскиз перейдите в 2-х мерный графический редактор, в котором будет производиться построение эскиза.

5. Включите кнопку Геометрические построения на панели инструментов.

6. На панели инструментов выбираем команду Ввод прямоугольника .

7. Размещаем левый нижний угол создаваемой грани куба в начало системы координат окна документа (команда <Ctrl+0> на цифровой клавиатуре (см. рис.77).

8. В Строке параметров прямоугольника вводим равные значения сторон граней куба (высота h=30 по команде Alt+h, ширина w=30 по команде Alt+w).

9. По команде Закончить редактирование в Панели управления программы Компас.

10. Для задания объема куба в Панели инструментов 3-х мерного Компаса выбираем команду Операция выдавливания .

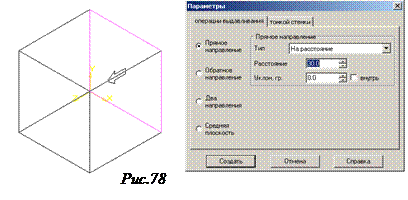11. В появившемся диалоговом окне Параметры для выдавливания куба задайте параметр глубины куба - На расстояние 30 мм (см.рис.78);

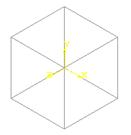
12. Нажмите кнопку Создать в диалоговом окне Параметры. Получили трехмерный куб без невидимых линий (см. рис.79).

Рис. 80

Рис. 79

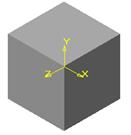
Примечания:*Цифровая клавиатура должна быть включена кнопкой Num Lock на клавиатуре.

**В Windows должна быть включена английская раскладка клавиатуры (команда Ctrl+Shift tили Alt+Shift).

***Чтобы видеть изображение эскиза квадрата, сдвиньте мышкой окно Параметры в сторону. В Строке состояния программы КОМПАС 3D LT выбрать ориентацию Изометрия.

13. Выберите в Панели управления программы команду Полутоновое . Вы получите трехмерный куб (см. рис.80).

УПРАЖНЕНИЕ 2.Построить трехмерные модели правильной и неправильной четырехгранной пирамид.

Рис.81

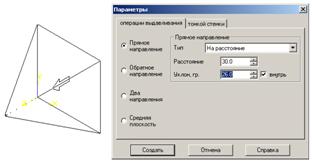Четырехгранная пирамида отличается от параллелепипеда и куба тем, что ее боковые грани сходятся в точку на вершине напротив основания. Для построения 4-хгранной пирамиды в начале выполняем п/п 1-9 упражнения №1 лаб. раб. №7 (строим эскиз основания пирамиды). Далее в диалоговом окне Параметры, добавляется действие, создающее уклон и одновременно убирающее грань параллелепипеда или куба, расположенную напротив основания (см.пп. № 10-1, 10-2).

10-1. Правильная пирамида строится из кубической модели. В диалоговом окне Параметры установите галочку в команде Уклон Внутрь и постепенно увеличивайте значение уклона, пока верхняя грань не сойдется в точку. Уберите для операции «тонкой стенки» галочку «создавать тонкую стенку» (см. рис.81).

11. Нажмите кнопку Создать в диалоговом окне Параметры. Получили правильную пирамиду без невидимых линий (см. рис.82), ее окрашенный вариант на рис.83.

Рис.81

12.Выберите в Панели управления программы команду Полутоновое . Вы получите трехмерную правильную пирамиду (см. рис.83).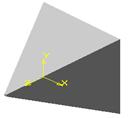

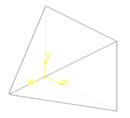10-2. Неправильная пирамида строится из

модели параллелепипеда. В диалоговом окне

Рис.83

Рис. 82

Параметры установите галочку в команде Уклон и постепенно увеличивайте значение Уклона, пока верхняя грань не сойдется в ребро. Уберите для операции «тонкой стенки» галочку «создавать тонкую стенку». Нажмите кнопку Создать в диалоговом окне Параметры. Получили неправильную пирамиду без невидимых линий (см. рис.84).

11. Выберите в Панели управления программы команду Полутоновое . Вы получите трехмерную неправильную пирамиду (см. рис.85).

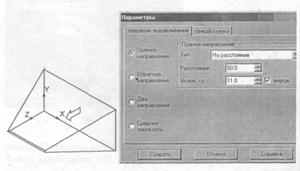
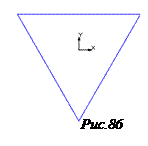УПРАЖНЕНИЕ 3.Построение трехмерной модели трехгранной призмы.

Повторите пп.1-4 упражнения №2 лаб. раб. №7. Видом спереди (т.е. основанием) трехгранной призмы выберем правильный треугольник (в панели инструментов – панели расширенных команд Ввод многоугольника).

Рис. 82

5. На панели инструментов выберите команду Ввод прямоугольника, далее, не отпуская ЛКМ, выбираем в панели расширенных команд Ввод многоугольника .

6. Размещаем центр многоугольника в начало системы координат окна документа (команда <Ctrl>+<0> на цифровой клавиатуре) см. рис.86.

7. В Строке параметров для многоугольника введите 3 грани (т.е. тре-

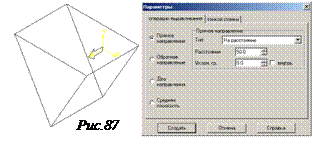угольник), введите значение радиуса описанной вокруг треугольника окружности r=30 по команде Alt+r и угла наклона треугольника а=90 градусов по команде Alt+а. Получаем треугольник – эскиз основания трехгранной призмы (см. рис.87).

8. Команда Закончить редактирование в Панели управления системы Компас.

Примечания:*Цифровая клавиатура должна быть включена кнопкой Num Lock на клавиатуре.

**В Windows должна быть включена английская раскладка клавиатуры (команда Ctrl+Shift tили Alt+Shift).

9. Задайте объем призмы. В панели инструментов трехмерного Компаса выбираем команду Операция выдавливания .

10. В появившемся диалоговом окне Параметры для выдавливания трехгранной призмы задайте параметр глубины трехгранной призмы – На расстояние 50мм. Уберите для операции «тонкой стенки» галочку «создавать тонкую стенку».

11. Нажмите кнопку Создать в диалоговом окне Параметры. Получили трехмерную модель трехгранной призмы без невидимых линий (см. рис.87).

12. Выберите в Панели управления программы команду Полутоновое . Вы получили трехмерную модель трехгранной призмы (см. рис. 88).

УПРАЖНЕНИЕ 4. Построение трехмерной модели трехгранной пирамиды.

Правильная трехгранная пирамида строится из модели трехмерной трехгранной призмы (см. упражнение 3, лаб.раб. №7).

10. В диалоговом окне Параметры установите галочку в команде Уклон Внутрь и постепенно увеличивайте значение уклона, пока верхняя грань не сойдется в точку. Уберите для операции «тонкой стенки» галочку «создавать тонкую стенку». Нажмите кнопку Создать в диалоговом окне Параметры. Получили правильную трехгранную пирамиду без невидимых линий (см. рис.89).

Рис. 89

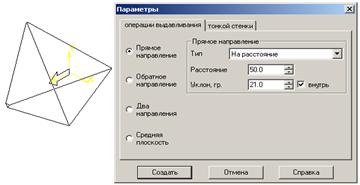
Примечания:*Цифровая клавиатура должна быть включена кнопкой Num Lock на клавиатуре.

**Аналогично построению трехмерных моделей трехгранной призмы строятся и другие правильные трехмерные N-гранные (4-,5-,6-,8-,9-,10-гранные) модели.

11.

Рис.90

Выберите в Панели управления программы команду Полутоновое . Вы получили правильную трехмерную трехгранную пирамиду (см. рис. 90).

ЗАДАНИЯ

ЗАДАНИЕ №1.Выполнить трехмерную модель параллелепипеда с параметрами: высота h= 20мм, ширина w= 30мм, глубина = 10мм.

ЗАДАНИЕ №2.Выполнить трехмерную модель куба с параметрами: высота h= 50мм, ширина w= 50мм, глубина = 50мм.

ЗАДАНИЕ №3.Выполнить трехмерную модель 8-гранной призмы с параметрами:радиус вписанной окружности основания 8-гранника rad= 50мм, угол наклона 8-гранника an= 90 градусов, высота призмы = 50мм.

ЗАДАНИЕ №4.Выполнить трехмерную модель 9-гранной пирамиды с параметрами: радиус вписанной окружности основания 9-гранника rad= 50мм, угол наклона 9-гранника an= 90 градусов, высота пирамиды - до схождения боковой стенки пирамиды в точку.

ЛАБОРАТОРНАЯ РАБОТА №8