Лабораторная работа № 3. Построение пирамиды и её плоских сечений
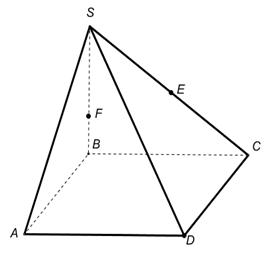
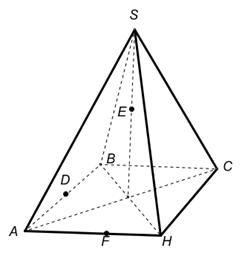
В соответствии с правилами параллельного проектирования изображение пирамиды строится следующим образом. Сначала строится основание. Это будет некоторый плоский многоугольник. Затем отмечается вершина пирамиды, которая соединяется боковыми ребрами с вершинами основания. На рисунке 1 показано изображение пятиугольной пирамиды.

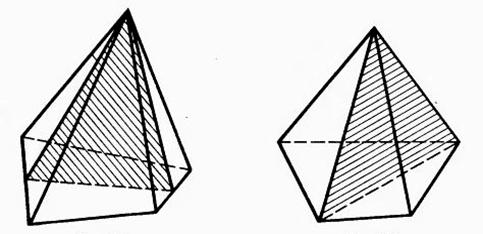
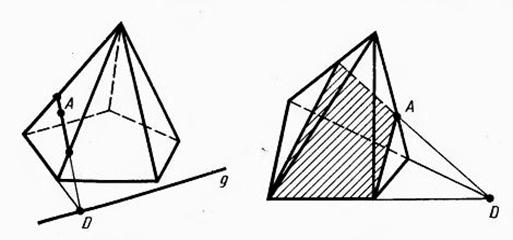
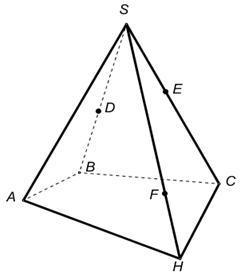
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники (рис. 2). В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды (рис. 3).
Сечение пирамиды плоскостью с заданным следом на плоскости основания строится так же, как и сечение призмы. Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.
Если на грани, не параллельной следу , известна какая-нибудь точка А, принадлежащая сечению, то сначала строится пересечение следа секущей плоскости с плоскостью этой грани – точка D на рисунке 4. Точка D соединяется с точкой А прямой. Тогда отрезок этой прямой, принадлежащий грани, есть пересечение этой грани с секущей плоскостью. Если точка А лежит на грани, параллельной следу, то секущая плоскость пересекает эту грань по отрезку, параллельному прямой. Переходя к соседней боковой грани, строят ее пересечение с секущей плоскостью и т.д. В итоге получается требуемое сечение пирамиды.
Внутреннее проектирование является центральным с центром проектирования в вершине пирамиды.
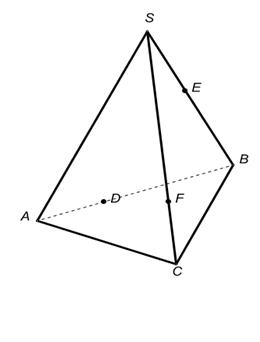
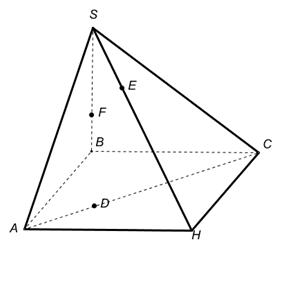
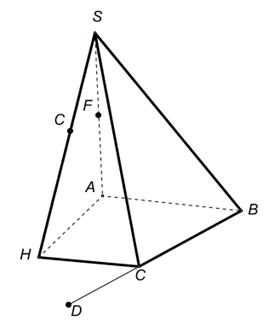
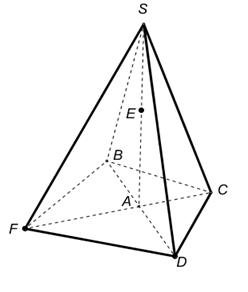
1.В некоторых случаях сечение удаётся построить, не прибегая к каким-либо специальным методам, а лишь основываясь на элементарных рассуждениях (и построениях), связанных с построением элементов пересечения прямых и плоскостей. Постройте сечения пирамиды плоскостями, проходящими через точки E, D, F.
 | 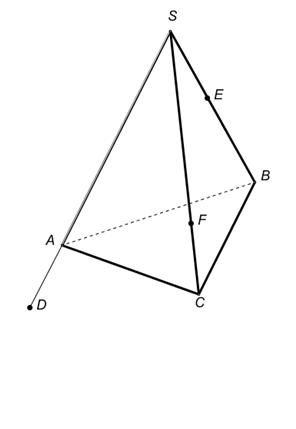 | 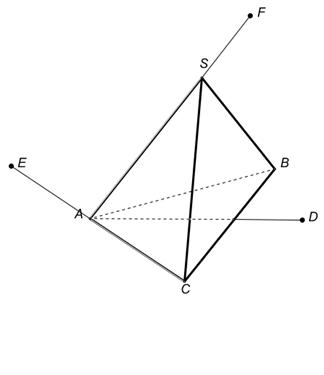 |
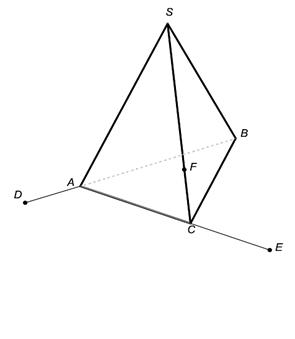 | 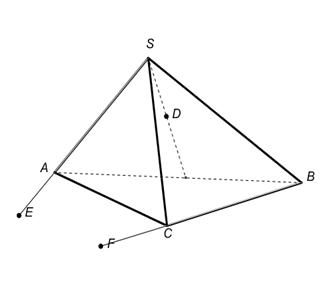 | 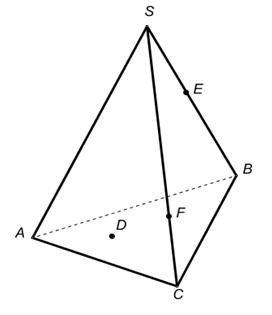 DÎАВС DÎАВС |
 |  |  |
 |  |  |
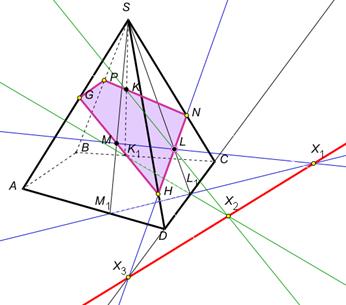
2. На рисунке показано построение методом следов сечения пирамиды плоскостью, проходящей через точкиК, L, M. Опишите этапы построения этого сечения.
 | ||
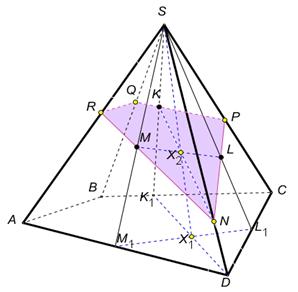
3. На рисунке показано построение методом внутреннего проектирования сечения пирамиды плоскостью, проходящей через точкиК, L, M. Опишите этапы построения этого сечения.
 | ||
4.Постройте сечения пирамиды плоскостью, проходящей через точки K, L, М. Дайте подробное решение одной из ниже приведённых задач на построение сечения. Для решения задачи желательно использовать интерактивную среду «1С: Математический конструктор».
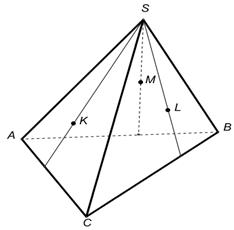 | 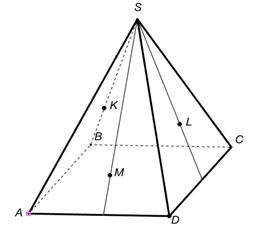 | 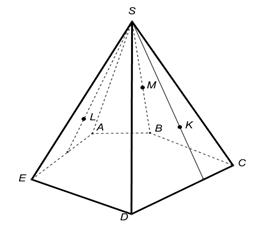 |
5. Внеаудиторное задание.Решить задачи №№ 56-60 из пособия Игошин В.И. Тетрадь по геометрии для 11 класса. Многогранники и их сечения, площади поверхностей, объёмы. – Саратов, 1997. – 64 с.
