Это поверхности, которые описываются какой-либо линией при ее вращении вокруг неподвижной оси.

а) При вращении прямой образуются:

· цилиндр вращения (прямая параллельна оси вращения);

· конус вращения (прямая пересекается с осью вращения).

б) При вращении окружности образуется:

· сфера (вращением окружности вокруг диаметра);

· тор (вращением окружности вокруг оси, лежащей в

плоскости окружности, но не проходящей через ее центр);

в) При вращении кривой второго порядка образуются:

· эллипсоид вращения (вращением эллипса);

· параболоид вращения (вращением параболы);

· однополостный гиперболоид;

· 2-х полостной гиперболоид.

Линейчатые поверхности

Это поверхности, описываемые какой -либо прямой (образующей) при ее движении в пространстве по какому-нибудь закону:

· цилиндрическая поверхность (образуется движением прямой линии по некоторой кривой линии, при этом прямая имеет постоянное направление);

· коническая поверхность (образуется движением прямой линии, проходящей через неподвижную точку, по некоторой кривой линии, называемой направляющей);

· торс и т.д.

Если направляющая линия является ломаной линией, то образуются:

· призматическая поверхность (образующая имеет постоянное направление);

· пирамидальная поверхность (образующая проходит через неподвижную точку).

Имеются и более сложные линейчатые поверхности:

· цилиндроид;

· коноид;

· косая плоскость и т. д.

Всякая прямая пересекается с такой поверхностью в двух точках, а плоскость пересекает ее по кривой второго порядка.

Поверхности второго порядка

·коническая поверхность (конус вращения и эллиптический конус, получаемый деформацией параллелей конуса вращения в эллипсы);

· цилиндрическая поверхность (цилиндр вращения, эллиптический, параболический и гиперболический цилиндры.

· эллиптический цилиндр может быть получен из цилиндра вращения деформацией его параллелей в эллипсы);

· эллипсоид (эллипсоид вращения, в частности сфера; трехосный эллипсоид, получаемый из эллипсоида вращения деформацией его параллелей в эллипсы);

· параболоид, гиперболоиды и др.

Винтовые поверхности

Они описываются какой-либо линией (образующей) при ее винтовом движении. Если образующая винтовой поверхности прямая линия, то поверхность называется линейчатой винтовой поверхностью или геликоидом (пример – шнек). Различают прямой и наклонный геликоиды. В первом случае образующая во всех положениях перпендикулярна осиt, во втором - пересекает ось геликоида под постоянным углом отличным от прямого.

Циклические поверхности

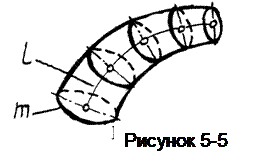Они описываются какой-либо окружностью (образующей) постоянного или переменного радиуса при ее произвольном движении.

К циклическим можно отнести все поверхности вращения и те из поверхностей второго порядка, которые имеют круговые сечения. Кроме этих к циклическим относят каналовые и трубчатые поверхности.

Каналовые поверхности(рисунок 5-5) образуются движением окружности переменного радиуса, центр которой 0 перемещается по заданной кривой (направляющей l ), а плоскость окружности остается перпендикулярной этой кривой.

Рисунок 4-5

Трубчатая поверхность образуется движением окружности постоянного радиуса – в этом ее отличие от каналовой поверхности.

Топографические поверхности

Образование их не подчинено какому-либо закону. К таким поверхностям относятся поверхности земной коры, корпуса судов, обшивки самолетов, автомобилей.

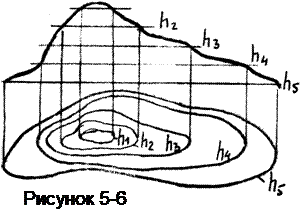На чертеже эти поверхности изображаются при помощи семейства некоторых линий (рисунок 5-6).