Ломаные и кривые линии (плоские и пространственные). винтовая линия.
ЛЕКЦИЯ №5
ЛОМАНЫЕ И КРИВЫЕ ЛИНИИ (ПЛОСКИЕ И ПРОСТРАНСТВЕННЫЕ). ВИНТОВАЯ ЛИНИЯ.
13. КИНЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ И ИХ ИЗОБРАЖЕНИЕ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ. классификация поверхностей.
ВЗАИМОПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПОВЕРХНОСТИ, ЛИНИИ И ПОВЕРХНОСТИ.
ЛОМАНЫЕ И КРИВЫЕ ЛИНИИ (ПЛОСКИЕ И ПРОСТРАНСТВЕННЫЕ). ВИНТОВАЯ ЛИНИЯ
Точку, прямую и плоскость называют элементарными геометрическими фигурами. Из них могут быть созданы все остальные геометрические фигуры.
Приняв в качестве элементарной фигуры точку, можно рассматривать любую линию как множество последовательных положений движущейся точки - траекторию точки.
Ломаная линия - линия, состоящая из отрезков прямой, расположенных в пространстве под некоторым углом друг к другу.
Кривыелинии - могут быть плоскими, когда все точки кривой лежат в одной плоскости, и пространственными - когда точки кривой не лежат в одной плоскости.
К плоским кривым относятся кривые второго порядка: окружность, эллипс, парабола, гипербола, синусоида, циклоида и т.д. Прямая, лежащая в плоскости этих линий, может пересечь любую из них лишь дважды. С построением этих линий вы уже ознакомились при выполнении задания №1 "Геометрическое черчение" в курсе машиностроительного черчения.
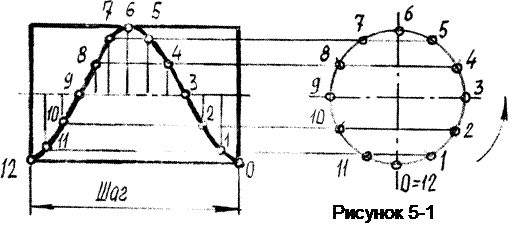
Из пространственныхкривых наиболее часто встречается на практике цилиндрическая винтовая линия. Если точка совершает равномерное движение по прямой, которая в свою очередь совершает равномерное вращение вокруг параллельной ей оси, то она (точка) опишет пространственную кривую – цилиндрическую винтовую линию (рисунок 5-1).
КИНЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ И ИХ ИЗОБРАЖЕНИЕ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ. классификация поверхностей
 |
Поверхность - множество точек, имеющее два измерения вдоль каких-либо линий этой поверхности.
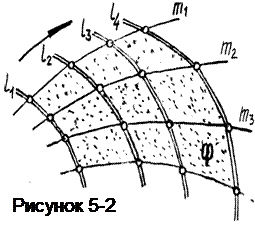В начертательной геометрии пользуются, в основном, кинематическим способом образования поверхностей, т.е. движением линии (рисунок 5-2). Поверхность Ф представляет собой множество последовательных положенийl1, l2, l3 и т.д. линииl, форма и движение которой подчинены некоторому закону. Линия l называется образующей. Линии, по которым она движется, называют направляющими –m1, m2, m3 и т.д.
Но в таком виде на чертеже поверхность обычно не задают.
Краткости и достаточной емкости геометрической информации о поверхности служат понятия определителя и ее каркаса.
Определитель поверхности - это минимальная, но достаточная информация о поверхности, необходимая для построения на ней любой ее точки.
Каркасом поверхности называют множество ее линий (например l и m, рисунок 5-2).
На комплексном чертеже поверхность обычно задают проекциями ее направляющих, и указывается способ построения ее образующих. Для придания чертежу большей наглядности строят на нем очеркповерхности.
Очерк поверхности - проекция ее контурной линии. Или иначе - это граница, отделяющая проекцию поверхности от остальной
 |
части плоскости.
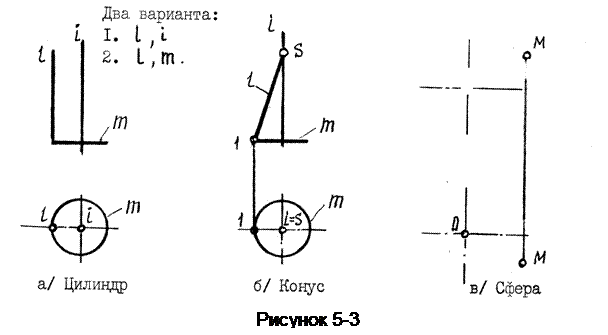
Примеры задания поверхностей вращения определителем представлены на рисунке 5-3.
 |
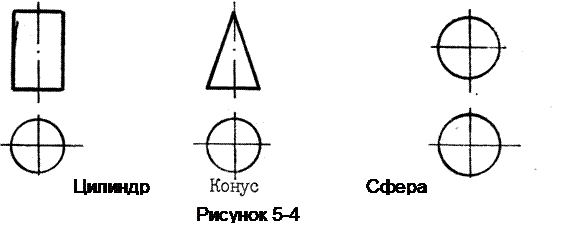Примеры чертежей поверхностей заданных очерком (рисунок 5- 4).
Для удобства изучения поверхностей их обычно делят на ряд классов. На примере поверхностей, которые встречаются в практике наиболее часто, рассмотрим эту классификацию.
Поверхности вращения
Линейчатые поверхности
Это поверхности, описываемые какой -либо прямой (образующей) при ее движении в пространстве по какому-нибудь закону:
· цилиндрическая поверхность (образуется движением прямой линии по некоторой кривой линии, при этом прямая имеет постоянное направление);
· коническая поверхность (образуется движением прямой линии, проходящей через неподвижную точку, по некоторой кривой линии, называемой направляющей);
· торс и т.д.
Если направляющая линия является ломаной линией, то образуются:
· призматическая поверхность (образующая имеет постоянное направление);
· пирамидальная поверхность (образующая проходит через неподвижную точку).
Имеются и более сложные линейчатые поверхности:
· цилиндроид;
· коноид;
· косая плоскость и т. д.
Всякая прямая пересекается с такой поверхностью в двух точках, а плоскость пересекает ее по кривой второго порядка.
Поверхности второго порядка
·коническая поверхность (конус вращения и эллиптический конус, получаемый деформацией параллелей конуса вращения в эллипсы);
· цилиндрическая поверхность (цилиндр вращения, эллиптический, параболический и гиперболический цилиндры.
· эллиптический цилиндр может быть получен из цилиндра вращения деформацией его параллелей в эллипсы);
· эллипсоид (эллипсоид вращения, в частности сфера; трехосный эллипсоид, получаемый из эллипсоида вращения деформацией его параллелей в эллипсы);
· параболоид, гиперболоиды и др.
Винтовые поверхности
Они описываются какой-либо линией (образующей) при ее винтовом движении. Если образующая винтовой поверхности прямая линия, то поверхность называется линейчатой винтовой поверхностью или геликоидом (пример – шнек). Различают прямой и наклонный геликоиды. В первом случае образующая во всех положениях перпендикулярна осиt, во втором - пересекает ось геликоида под постоянным углом отличным от прямого.
Циклические поверхности
Они описываются какой-либо окружностью (образующей) постоянного или переменного радиуса при ее произвольном движении.
К циклическим можно отнести все поверхности вращения и те из поверхностей второго порядка, которые имеют круговые сечения. Кроме этих к циклическим относят каналовые и трубчатые поверхности.
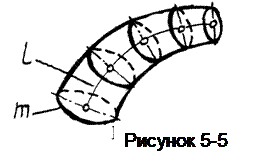
Каналовые поверхности(рисунок 5-5) образуются движением окружности переменного радиуса, центр которой 0 перемещается по заданной кривой (направляющей l ), а плоскость окружности остается перпендикулярной этой кривой.
|
Топографические поверхности
Образование их не подчинено какому-либо закону. К таким поверхностям относятся поверхности земной коры, корпуса судов, обшивки самолетов, автомобилей.
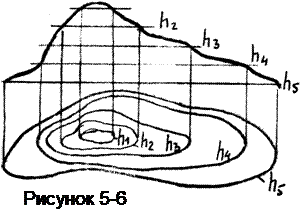На чертеже эти поверхности изображаются при помощи семейства некоторых линий (рисунок 5-6).
ЛЕКЦИЯ №5
ЛОМАНЫЕ И КРИВЫЕ ЛИНИИ (ПЛОСКИЕ И ПРОСТРАНСТВЕННЫЕ). ВИНТОВАЯ ЛИНИЯ.
13. КИНЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ И ИХ ИЗОБРАЖЕНИЕ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ. классификация поверхностей.