Тема 1.7 Пересечение поверхностей

Сечение поверхностей плоскостями

Сечениеповерхностейплоскостямичастногоиобщегоположения является одной из главных тем начертательной геометрии. Основой этой темыявляютсяконические,цилиндрические,сферическиеиторовые сечения.Наглядноеизображениесеченийупомянутыхповерхностей представлено на рисунке 85.

Самойинтереснойповерхностью,сточкизренияразнообразия сечений, является поверхность прямого кругового конуса.

Еслисекущаяплоскостьпроходитпараллельнооснованию,тов сечении получается окружность, радиус которой равен расстоянию от оси конуса до образующей вдоль следа секущей плоскости.

Если секущая плоскость не параллельна основанию и пересекает обе очерковыеобразующие,товсеченииполучаетсяэллипс.Плоскость, параллельная оси конуса, в сечении образует гиперболу.

Если секущая плоскость пересекает одну из образующих и угол её наклонаравенуглунаклонаобразующей,товсеченииобразуется парабола.

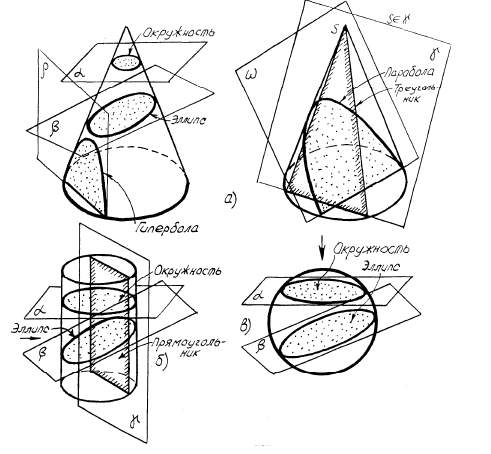
Плоскость,проходящаячерезвершинуконуса,всеченииобразует треугольник.

Рисунок 85 – Сечение поверхностей

Пересечение прямой с поверхностью

Задачапересеченияпрямойсповерхностьюрешаетсяаналогично задачеопересечениипрямойсповерхностьюмногогранников.Отличие состоитвтом,чтовсечениикривойповерхностивспомогательной плоскостьювбольшинствеслучаевобразуютсякривыелинии.Общая методика решения задачи представлена на рисунке 86, а.

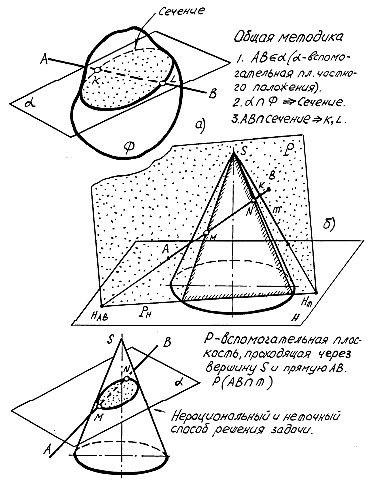
Рисунок 86 – Пересечение прямой с поверхностью

Пересечение поверхностей

Задача о пересечении поверхностей является наиболее значительной вкурсеначертательнойгеометриикакстеоретической,такис практическойточекзрения.

Линия, общая для обеих пересекающихся поверхностей, называется линиейпересечения.Построениелинийпересеченияиихразметкана различныхметаллоконструкцияхявляетсяоднойизглавныхисложных инженерных задач.

Существуютразличныечастныеслучаипересеченияповерхностей, обусловленныегеометрическимииматематическимизакономерностями (рисунок 87).

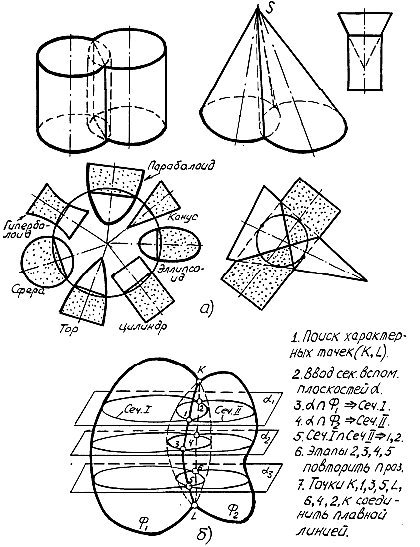
Двецилиндрическиеповерхностиспараллельнымиосями пересекаютсяпопрямымлиниям,соединяющимточкипересечения основанийцилиндров.Двеконическиеповерхностисобщейвершиной пересекаютсяпопрямымлиниям,соединяющимвершинуиточки пересечения оснований. Соосные поверхности вращения второго порядка пересекаютсяпоокружностям,фронтальнаяпроекциякоторыхявляется прямыми линиями.

Рисунок 87 – Частные случаи пересечения поверхностей (а) и построение линии пересечения методом секущих вспомогательных плоскостей (б)

Вначертательнойгеометрииразработаномножествометодов построения линий пересечения поверхностей. Самыми распространенными методами являются метод секущих вспомогательных плоскостей и метод концентрических сфер.

Сущность метода вспомогательных секущих плоскостей заключается втом,чтоприпомощисекущихплоскостейнаходятсяобщиеточки, принадлежащиепересекающимсяповерхностям.Наглядносутьметода представлена на рисунке 87, б. Он содержит общий порядок решения:

1) Поиск характерных точек и построение их проекций (точки K и L);

2) Вводсекущейвспомогательнойплоскости.Вкачестве вспомогательныхплоскостейберутплоскостичастногоположения, которыеобразуютвсеченияхповерхностейпростыефигуры (принцип простых сечений);

3) Строят сечения поверхностей вспомогательной плоскостью (Сеч.I и Сеч.II);

4) Находят общие точки обоих сечений (точки 1 и 2);

5) Пункты 2, 3, 4 повторяют несколько раз (в учебных чертежах 5-7 раз) c новыми вспомогательными плоскостями;

6) Полученныеточкисоединяютплавнойлиниейсучетом видимости проекций.

Вкачествевспомогательныхповерхностейвыбираюттакие,линии пересечения которых с заданными поверхностями проецируются в графически простые линии – прямые, окружности, т.к. при этих условиях задача решается проще и точнее. В качестве вспомогательных поверхностей можно использовать плоскости или сферы.

Рассмотримприменениевспомогательныхсекущихплоскостейна примере построения линии пересечения сферы с конусом вращения (рисунок 88).

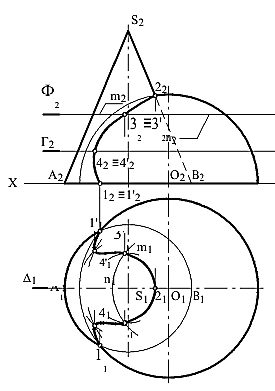
Рисунок 88 – Метод вспомогательных секущих плоскостей

Припостроенииточеклиниипересеченияповерхностивначале находяттеточки,которыеназываютхарактернымиилиопорными.Основания заданных поверхностей, представленных окружностями, принадлежатгоризонтальнойплоскостипроекцийП₁.Впересечении окружностей основания получаем опорные точки 1₁ и 1'₁. По линии связи переносим эти точки на фронтальную проекцию.

Проведенная фронтальная плоскость уровня ∆ (∆1), проходящая черезоськоническойповерхностиицентрсферы,пересекаетконическую поверхность по контурным образующим SA и SB, а сферу – по окружности,совпадающейспроекциейглавногомеридиана.Впересеченииконтурной образующей SB и главного меридиана получим опорную точку 2(2₁, 2₂) – наивысшую точку линии пересечения.

Промежуточные точки найдем при помощи горизонтальных плоскостей уровня Ф и Г, которые пересекают заданные поверхности по окружностям. При взаимном пересечении этих окружностей получают промежуточные точки искомой линии. Вначале находим горизонтальные проекции 3₁ и 3'₁ точек 3 и 3' на пересечении окружностей m₁ и n1, получающихся от пересечения плоскостью Ф конуса и сферы. Затем, используя линии связи и принадлежность этих точек плоскости Ф, находим их фронтальные проекции 32 и 3'2.

Числовспомогательныхсекущихплоскостей,а,следовательно,и промежуточных точек линии пересечения зависит от требуемой точности решения.

Относительно горизонтальной плоскости проекций видимой является заданная половинка сферы и коническая боковая поверхность. Следовательно, видима и вся горизонтальная проекция линии пересечения этих поверхностей.

Относительнофронтальнойплоскостипроекцийвидимойявляется часть 1, 4, 3, 2, фронтальная проекция линии пересечения, расположенная на видимых (передних) участках заданных поверхностей, а часть 1', 4', 3', 2' невидима.

Заданныеповерхностисимметричныотносительнофронтальной плоскостиуровня ∆,проходящейчерезосиихвращения,следовательно, симметричнаилинияихпересеченияотносительноэтойжеплоскости.

Значит, на фронтальной плоскости проекций П2 проекции видимой и невидимой частей линии пересечения совпадут и будут кривой второго по рядка.

На чертеже одноименные проекции точек 1₁, 4₁, 3₁, 2₁, 3'₁, 4'₁, 1'₁ и 1₂1'₂, 4₂4'₂, 3₂3'₂ и 2₂ соединяем плавной сплошной основной линией и получаем искомые проекции линии пересечения.

Методконцентрическихсфероснованначастномслучае пересечения поверхностей (пересечение тел вращения со сферой, когда ось тел проходит через центр сферы).

Спомощьювспомогательныхсферическихповерхностейудобно строить линии пересечения двух поверхностей вращения с общей плоскостью симметрии, параллельной одной из плоскостей проекций.

При этом возможны два случая:

1) если оси поверхностей вращения пересекаются, то для построения линии пересечения этих поверхностей применяют семейство концентричных сфер;

2) если оси поверхностей вращения не пересекаются, то используютэксцентрические сферы.

План решения задачи способом концентрических сфер следующий:

1) принимая точку пересечения осей заданных поверхностей за центр, строим вспомогательные сферы – посредники;

2) определяем окружности, по которым пересекаются сферы-посредники с каждой из заданных поверхностей;

3) находим общиеточки пересечения полученных окружностей.

Эти точки и принадлежат искомой линии пересечения поверхностей.

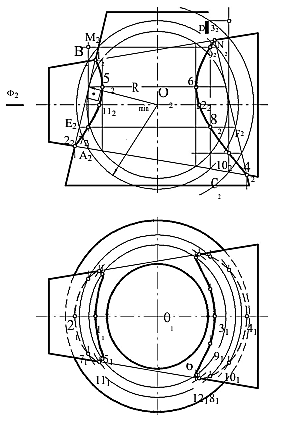
На рисунке 89 построена линия пересечения двух конусов вращения, осикоторых пересекаются, образуя общую фронтальную плоскость симметрии.

Рисунок 89 – Метод концентрических сфер

В данном случае применены вспомогательные сферы, проведенные из одного и того же центра – точки О (О₂) пересечения осей конусов. Диапазон радиусов сфер определяется минимальным и максимальным радиусами. Минимальный радиус секущей сферы назначается из условия касаниясферыоднойипересечениядругойпересекающейсяповерхности. Максимальнымрадиусомявляетсяотрезокпрямойотцентрасферыдо наиболее удаленной точки пересечения очерков пересекающихся поверхностей. Окружности, по которым сферы пересекают одновременно две поверхности,проецируютсянафронтальнуюплоскостьпроекцийввидепрямолинейных отрезков.

Точкипересеченияфронтальныхпроекцийочерковыхобразующих 1₂2₂3₂4₂ являются высшими и низшими точками линии пересечения. Точки 5₂6₂ на фронтальной проекции, наиболее близко расположенные к оси вертикального конуса, определены с помощью сферы радиуса R_min, вписанной в этот конус. Промежуточные точки 7₂8₂9₂ получены при помощи сферы радиусаR,очерккоторойнафронтальнойпроекцииизобразитсяввиде окружности этого же радиуса. Сфера радиуса R пересечет горизонтальный конус по окружности диаметра АВ и CD, а вертикально расположенный конус – по окружности EF и MN. В пересечении полученных проекций окружностей – отрезков А₂В₂ и C₂D₂ с E₂F₂ и M₂N₂ – получаем искомые точки 7₂8₂9₂ линии пересечения.

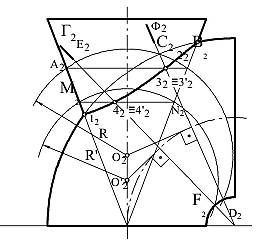
Пример построения линии пересечения двух поверхностей вращения способом эксцентрических сфер приведен на рисунке 90 (открытый тор пересекается с конусом вращения).

Рисунок 90 – Метод эксцентрических сфер

Поверхности имеют одну общую плоскость симметрии. Оси пересекающихся поверхностей вращения между собой не пересекаются. Поверхности заданы фронтальными отрезками.

Припостроениилиниипересеченияповерхностей прежде всего определяемточки1и2пересеченияочерковыхобразующихповерхностей.

Затем через ось вращения тора проводим фронтально-проецирующую плоскость Ф. Она пересекает тор по окружности. Центры сфер, пересекающих тор поокружности,находятсянаперпендикуляре, восстановленном в центре окружности к плоскости Ф. Пересечение этого перпендикуляра с осью конуса вращения даст центр О (О₂) вспомогательной секущей сферы с радиусом R.

Такаясферапересекаеткактор, так и конус вращения по окружностям, фронтальные проекции которых – отрезки А₂В₂ и C₂D₂ прямых. Точки 3₂ и 3'₂пересеченияокружностейпринадлежатфронтальнойпроекциилиниипересечения поверхностей.

Аналогично определяют другие промежуточные точки линии пересечения поверхностей. Вспомогательные сферы имеют различные центры, находящиеся на оси конуса вращения.