Определение расстояния от точки до плоскости
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Методические указания
к практическим занятиям и самостоятельной работе
студентов очной и заочной форм обучения
для студентов специальностей 190202.65, 190201.65
и направлений 220400.62, 220700.62, 221700.62, 151900.62, 150700.62, 190600.62, 190700.62
Курган 2013
Кафедра: «Начертательная геометрия и инженерная графика»
Дисциплина: «Начертательная геометрия»
150700.62
«Начертательная геометрия и инженерная графика»
190202.65, 190201.65, 151900.62, 190600.62, 190700.62
«Инженерная и компьютерная графика»
220400.62, 220700.62, 221700.62
Составили: ст. преподаватель И.Е. Карпова, ассистент Е.К. Карпов.
Утверждены на заседании кафедры « 24 » октября 2013 г.
Рекомендованы методическим советом университета 12 декабря 2013 г.
ВВЕДЕНИЕ
Начертательная геометрия относится к базовым общетехническим дисциплинам и представляет собой один из разделов геометрии, в котором окружающие нас пространственные формы, состоящие из совокупности точек, линий, поверхностей, изучаются по их изображениям на плоском чертеже. Она является грамматикой чертежа как языка техники, что делает освоение дисциплины обязательным при получении инженерных знаний.
В данном методическом указании рассматривается решение некоторых метрических и позиционных задач начертательной геометрии.
МЕТРИЧЕСКИЕ ЗАДАЧИ
Метрическими принято считать задачи, решение которых связано с необходимостью измерять расстояния, строить отрезки заданной длины, строить перпендикуляры к прямой и к плоскости, определять натуральные величины плоскостей, углов и расстояний между ними.
Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций
Задача Определить натуральную величину отрезка АВ и его углы наклона к плоскостям проекций.
Алгоритм решения задачиНатуральная величина отрезка прямой всегда может быть принята за гипотенузу прямоугольного треугольника, одним катетом которого является отрезок, равный и параллельный проекции, а другим – разность расстояний концов отрезка до плоскости проекций (рисунок 1 а, б).
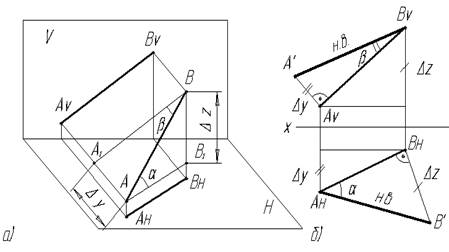
а) в диметрии б) на эпюре
Рисунок 1 – Определение натуральной величины отрезка и углов
наклона;
В прямоугольном треугольнике АВВ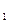 
– катет АВ 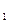= АнВн; катет ВВ 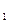= =.Zв – Zа = ∆Z; гипотенуза АВ – натуральная величина отрезка, α – угол наклона прямой АВ к плоскости Н.
В прямоугольном треугольнике АВА 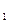– сторона А 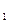В = AvBv; сторона А 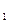А = Yа – Yв = ∆Y; сторона АВ – натуральная величина отрезка; β – угол наклона прямой к плоскости V.
Определение расстояния от точки до плоскости
Задача Определить расстояние от точки А до заданной плоскости (рисунок 2).
Алгоритм решения задачи
1 В плоскости треугольника АВС построить проекции главных линий плоскости (фронтали и горизонтали).
2 На основании теоремы о прямом угле строим проекции перпендикуляра к данной плоской фигуре.
3 Находим точку пересечения перпендикуляра, проведенного из точки А с заданной плоскостью (точка I).
4 Определяем натуральную величину отрезка IА.
Рисунок 2 – Определение расстояния от точки до плоскости
Алгоритм решения задачи
1 Провести горизонталь А1 в треугольнике АВС.
2 Горизонталь А’H1’H построить перпендикулярно фронтальной плоскости на произвольном расстоянии от нее.
3 Методом засечек относительно горизонтали А’Н1’Н перенести горизонтальную проекцию треугольника в положение А’НВ’НС’Н (АНВНСН = =А’НВ’НС’Н). По горизонтальной проекции треугольника построить его фронтальную проекцию. При этом перемещении плоскость общего положения преобразовали во фронтально-проецирующую плоскость.
4 Перенести новую фронтальную проекцию треугольника А’VВ’VC’Vв положение А’’VВ’’VС’’V, параллельное горизонтальной плоскости проекций (плоскость уровня), достроить горизонтальную проекцию А’’НВ’’НС’’Н. Горизонтальная проекция А’’НВ’’НС’’Н будет являться натуральной величиной треугольника АВС(рисунок 4).
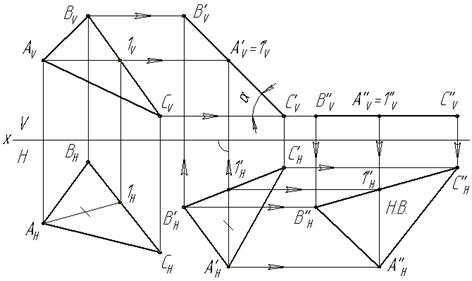
Рисунок 4 – Определение натуральной величины треугольника способом плоскопараллельного перемещения
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Методические указания
к практическим занятиям и самостоятельной работе
студентов очной и заочной форм обучения
для студентов специальностей 190202.65, 190201.65
и направлений 220400.62, 220700.62, 221700.62, 151900.62, 150700.62, 190600.62, 190700.62
Редактор Е. А. Могутова
Подписано в печать Формат 60х84 1/16 Бумага тип. №1
Печать цифровая Усл. печ. л. 1,0 Уч.-изд. л. 1,0
Заказ Тираж 37 Не для продажи
РИЦ Курганского государственного университета.
640669, г. Курган, ул. Гоголя, 25.
Курганский государственный университет.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Методические указания
к практическим занятиям и самостоятельной работе
студентов очной и заочной форм обучения
для студентов специальностей 190202.65, 190201.65
и направлений 220400.62, 220700.62, 221700.62, 151900.62, 150700.62, 190600.62, 190700.62
Курган 2013
Кафедра: «Начертательная геометрия и инженерная графика»
Дисциплина: «Начертательная геометрия»
150700.62
«Начертательная геометрия и инженерная графика»
190202.65, 190201.65, 151900.62, 190600.62, 190700.62
«Инженерная и компьютерная графика»
220400.62, 220700.62, 221700.62
Составили: ст. преподаватель И.Е. Карпова, ассистент Е.К. Карпов.
Утверждены на заседании кафедры « 24 » октября 2013 г.
Рекомендованы методическим советом университета 12 декабря 2013 г.
ВВЕДЕНИЕ
Начертательная геометрия относится к базовым общетехническим дисциплинам и представляет собой один из разделов геометрии, в котором окружающие нас пространственные формы, состоящие из совокупности точек, линий, поверхностей, изучаются по их изображениям на плоском чертеже. Она является грамматикой чертежа как языка техники, что делает освоение дисциплины обязательным при получении инженерных знаний.
В данном методическом указании рассматривается решение некоторых метрических и позиционных задач начертательной геометрии.
МЕТРИЧЕСКИЕ ЗАДАЧИ
Метрическими принято считать задачи, решение которых связано с необходимостью измерять расстояния, строить отрезки заданной длины, строить перпендикуляры к прямой и к плоскости, определять натуральные величины плоскостей, углов и расстояний между ними.
Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций
Задача Определить натуральную величину отрезка АВ и его углы наклона к плоскостям проекций.
Алгоритм решения задачиНатуральная величина отрезка прямой всегда может быть принята за гипотенузу прямоугольного треугольника, одним катетом которого является отрезок, равный и параллельный проекции, а другим – разность расстояний концов отрезка до плоскости проекций (рисунок 1 а, б).
а) в диметрии б) на эпюре
Рисунок 1 – Определение натуральной величины отрезка и углов
наклона;
В прямоугольном треугольнике АВВ 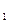– катет АВ 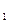= АнВн; катет ВВ 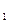= =.Zв – Zа = ∆Z; гипотенуза АВ – натуральная величина отрезка, α – угол наклона прямой АВ к плоскости Н.
В прямоугольном треугольнике АВА 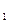– сторона А 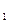В = AvBv; сторона А 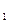А = Yа – Yв = ∆Y; сторона АВ – натуральная величина отрезка; β – угол наклона прямой к плоскости V.
Определение расстояния от точки до плоскости
Задача Определить расстояние от точки А до заданной плоскости (рисунок 2).
Алгоритм решения задачи
1 В плоскости треугольника АВС построить проекции главных линий плоскости (фронтали и горизонтали).
2 На основании теоремы о прямом угле строим проекции перпендикуляра к данной плоской фигуре.
3 Находим точку пересечения перпендикуляра, проведенного из точки А с заданной плоскостью (точка I).
4 Определяем натуральную величину отрезка IА.
Рисунок 2 – Определение расстояния от точки до плоскости