Практическое занятие № 4. Сопряжения

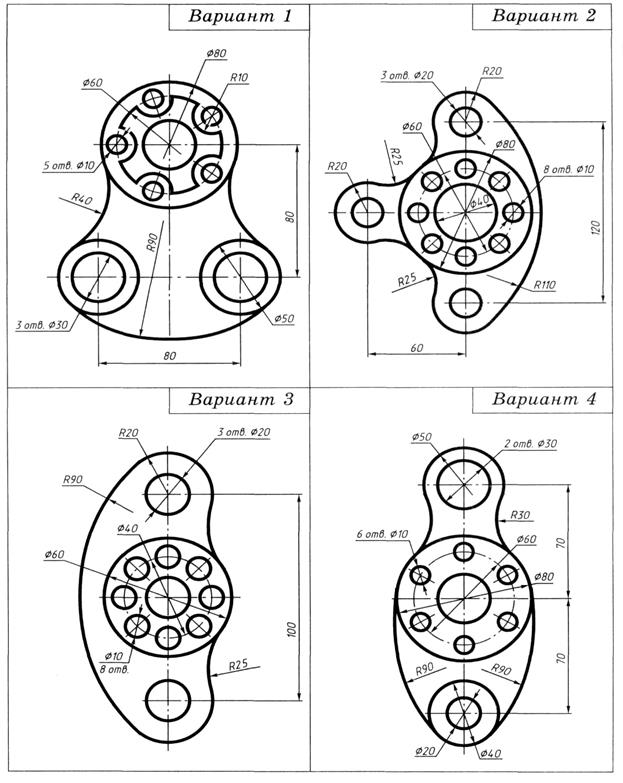
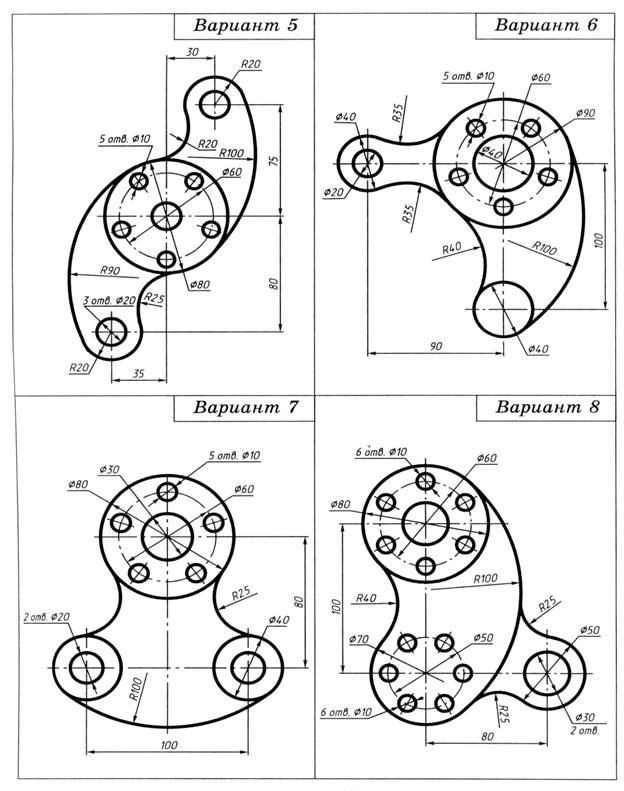
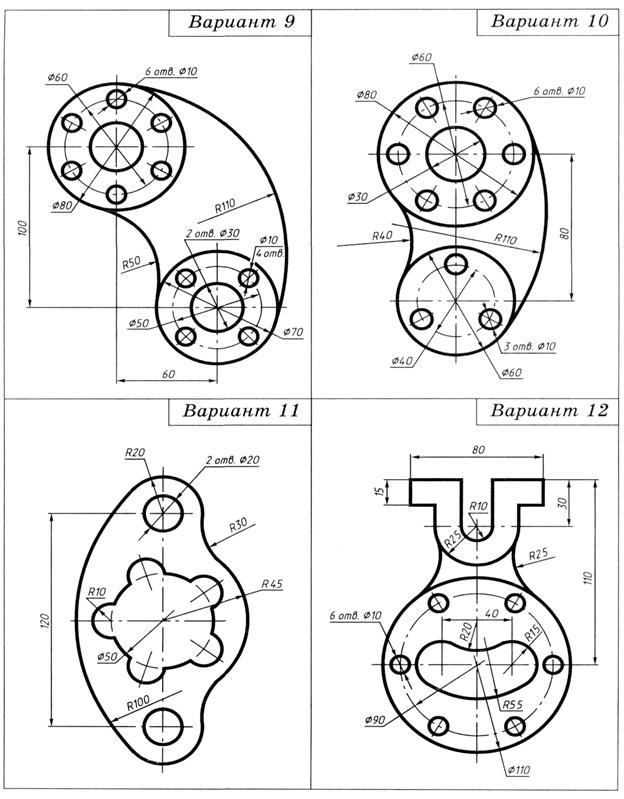
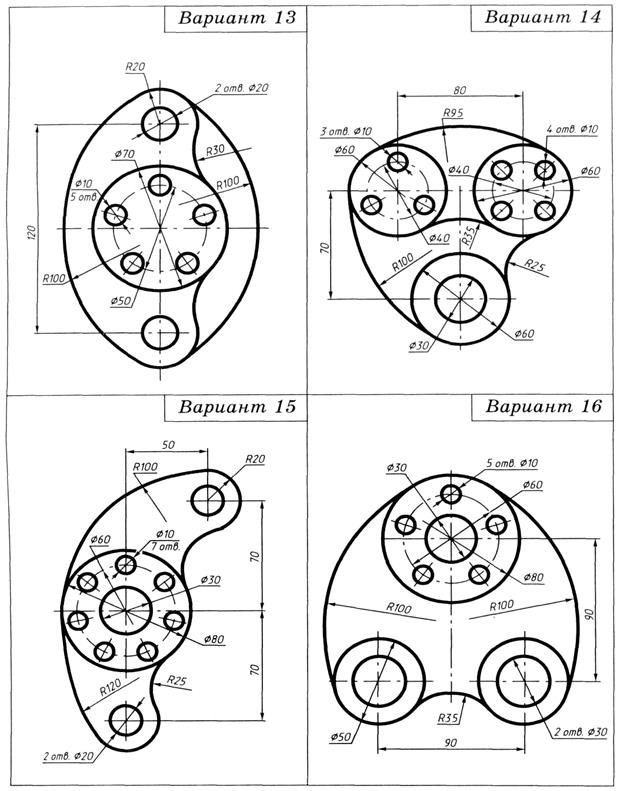
На формате А4 вычертить контур технической детали с построением сопряжений и делением окружности на равные части.

Сопряжением называется плавный переход одной линии в другую. Общая точка этих линий называется точкой сопряжения или точкой перехода. Приемы выполнения сопряжений показаны на рис. 80.

Построение прямой, касающейся дуги окружности в данной точке. Для проведения касательной к окружности параллельно данной прямой MN нужно из центра О окружности опустить перпендикуляр на данную прямую. Пересечение перпендикуляра с дугой окружности определит точку касания 1 (рис. 80, а).

Построение окружности, касательной к данной прямой. Геометрическим местом центров окружностей, касательных к данной прямой, является прямая, параллельная данной и отстоящая от нее на расстояние радиуса окружности R. Для определения точки касания из намеченного центра опускаем перпендикуляр на прямую и проводим окружность радиусом R (рис. 80, г).

Построение сопряжения двух дуг окружностей. Точки касания двух дуг окружностей находятся на линии центров ОО1или на продолжении этой линии центров (рис. 80, б, в). Дуги могут иметь внешнее (рис. 80, б) и внутреннее (рис. 80, в) касания. При внешнем касании расстояние между центрами ОО1равно сумме радиусов сопрягаемых дуг, при внутреннем — разности радиусов сопрягаемых дуг.

Построение сопряжения двух параллельных прямых дугой. Для сопряжения параллельных прямых AB и CD (рис. 80, д) к ним проводят перпендикуляр EF. Прямая EF параллельные прямые в точках сопряжений n и n1. Поделив прямую nn1пополам, получаем центр сопряжения параллельных прямых.

Построение сопряжения двух пересекающихся прямых дугой заданного радиуса. Такое сопряжение называют также скруглением углов. Центр скругления О находят в точке пересечения прямых, проведенных параллельно заданным прямым на расстоянии от них, равном радиусу скругления R (рис. 80, е, ж). Точки сопряжения 1 и 2 находятся на пересечении перпендикуляров из центра О к сопрягаемым сторонам.

Построение сопряжения дуги окружности с прямой с помощью дуги заданного радиуса и точки сопряжения. Центр дуги сопряжения О1должен лежать на перпендикуляре к заданной прямой, восстановленном из точки сопряжения А (рис. 80, з). Центр дуги сопряжения лежит на пересечении прямых, одна из которых проходит через центр окружности О и точку сопряжения А, а вторая является биссектрисой угла, образованного данной прямой и касательной, проведенной через точку А.

Рис. 80. Построение сопряжений

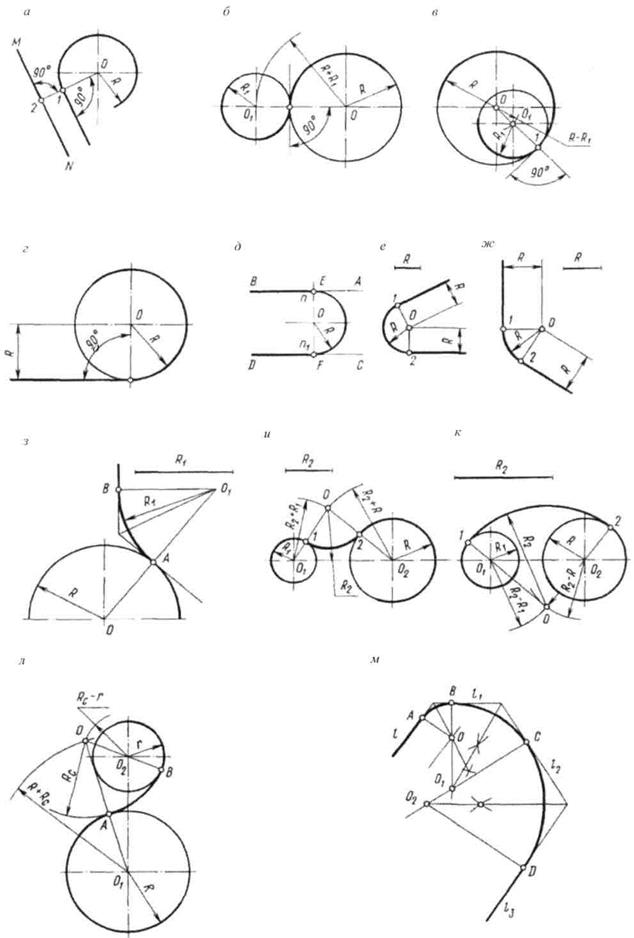Построение сопряжения двух дуг окружностей дугой сопряжения заданного радиуса R2. В случае внешнего сопряжения (рис. 80, и) из центров дуг О1и О2радиусами, равными R + R2и R1+ R2проводят дуги, пересечение которых определяет центр сопрягаемой дуги О. Точки сопряжений 1 и 2 находятся на линиях О1О и О2О, соответственно. В случае внутреннего сопряжения (рис. 80, к) из центров О1и О2радиусами, равными R2— R1и R2— R проводят дуги, точка пересечения которых определяет центр сопрягаемой дуги О. Точки сопряжений 1 и 2 находятся на продолжениях линий, соединяющих центры ОО1и ОО2. В случае внутреннего и внешнего сопряжения (рис. 80, л) требуется провести дугу сопряжения радиуса RСтак, чтобы она имела с одной окружностью внутреннее, а с другой — внешнее сопряжение. Центр этой дуги находится в точке пересечения дуг, описанных из центра О1радиусом RC+ R и из центра О2радиусом RC— r. Точки сопряжений А и В лежат на линии ОО1и продолжении линии ОО2, соответственно.

Построение сопряжения дугами окружностей четырех пересекающихся прямых. Произвольно выбранная точка Она биссектрисе угла между прямыми l и l1может служить первым центром сопряжения (рис. 80, м). Перпендикуляры, опущенные из этого центра на прямые l и l1, дают точки сопряжений А и В. Второй центр дуги сопряжения О1находят на пересечении биссектрисы угла между прямыми l1и l2с продолжением перпендикуляра ВО. Третий центр дуги сопряжения О2определяют в точке пересечения биссектрисы угла между прямыми l2и l3с продолжением перпендикуляра О1С.

Задание 4