А.н. шинкевич, о.в. кривенок

А.Н. ШИНКЕВИЧ, О.В. КРИВЕНОК

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
И ЧЕРЧЕНИЕ

Методическое пособие по проведению практических занятий

для студентов специальности 1-19 01 01 «Дизайн» специализация «Дизайн интерьеров»

Минск

Современные знания

УДК 514

Н 36

Р е ц е н з е н т ы:

Жарков Н.И., кандидат технических наук, доцент,
заведующий кафедрой инженерной графики
Белорусского государственного технологического университета;

Климин Р.М., доцент кафедры интерьера и оборудования
Белорусской государственной академии искусств.

Шинкевич, А.Н.

Н 36 Начертательная геометрия и черчение: метод. пособие для студентов специальности 1-19 01 01 «Дизайн» специализация «Дизайн интерьеров» / А.Н. Шинкевич,
О.В. Кривенок. — Минск: Современные знания, 2009. — 15249 с.

ISBN 978-985-6885-46-7

Приводятся основные сведения о начертательной геометрии и черчении, инструменты и материалы, использующиеся в графических работах. Описываются виды конструкторских документов, а также стандартные масштабы выполнения чертежей, примеры выполнения и задания по практическим работам дисциплины.

Для студентов вузов.

УДК 514

ISBN 978-985-6885-46-7

© Шинкевич А.Н., Кривенок О.В., 2009

© ЧУО «Институт современных знаний

имени А.М. Широкова», 2009

© Оформление. ЗАО «Современные знания», 2009

Содержание

ПРЕДИСЛОВИЕ. 4

Раздел I. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.. 3

Методы проецирования. 3

Комплексный чертеж.. 5

Позиционные задачи. 7

Проецирование плоскости. 14

Метрические задачи. 19

Многогранники. 22

Тела вращения. 27

Аксонометрические проекции. 31

Задачи для самостоятельного решения. 33

Раздел II. ЧЕРЧЕНИЕ. 43

Введение в раздел «Черчение». 43

ОБЩИЕ СВЕДЕНИЯ.. 45

Карандаши чертежные. 45

Чертежная бумага. 46

Линейки и треугольники. 46

Готовальни. 46

ОБЩИЕ СВЕДЕНИЯ ПО ИНЖЕНЕРНОЙ ГРАФИКЕ. 48

Виды конструкторских документов. 48

Форматы.. 49

Масштабы.. 50

Линии. 51

Графические обозначения материалов. 54

Основные надписи. 57

Шрифты.. 61

Надписи на чертежах. 68

Размеры на чертежах. 69

Задания по разделу «Черчение». 73

ЛИТЕРАТУРА.. 146

ПРЕДИСЛОВИЕ. 4

Раздел I. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.. 3

Методы проецирования. 3

Комплексный чертеж.. 5

Раздел II. ЧЕРЧЕНИЕ. 43

Введение в раздел «Черчение». 43

ОБЩИЕ СВЕДЕНИЯ.. 45

Карандаши чертежные. 45

Чертежная бумага. 46

Линейки и треугольники. 46

Готовальни. 46

ОБЩИЕ СВЕДЕНИЯ ПО ИНЖЕНЕРНОЙ ГРАФИКЕ. 48

Виды конструкторских документов. 48

Форматы.. 49

Масштабы.. 50

Линии. 51

Графические обозначения материалов. 54

Основные надписи. 57

Шрифты.. 62

Надписи на чертежах. 69

Размеры на чертежах. 70

Задания по разделу «Черчение». 74

ЛИТЕРАТУРА.. 147

ПРЕДИСЛОВИЕ

Одной из основных учебных дисциплин, формирующих пространственное мышление и образное представление будущих дизайнеров, является дисциплина «Начертательная геометрия и черчение». Дизайнер интерьера в своей профессиональной деятельности реализует полученные в высшем учебном заведении знания в практической сфере проектирования.

Теоретической основой построения изображений на чертежах является начертательная геометрия — наука о способах построения объемных объектов на двумерной плоскости и решения с помощью этих изображений различных задач. К таким задачам относятся позиционные — установление относительного положения объектов, и метрические — определение расстояний, углов, натуральных величин плоских фигур, построение разверток поверхностей.

Потребность сохранять и передавать информацию о геометрических свойствах трехмерных форм путем условного изображения их на плоскости возникла еще в глубокой древности. Она вытекала из практической деятельности людей — необходимости сооружения жилищ и укреплений, храмов и памятников, развития искусств, а позже — из запросов техники. С разработкой или описанием способов изображения пространственных форм на плоскости связана деятельность многих ученых древности: Эсхила, Анаксагора, Демокрита, Элиодора Ларисского, Евклида, Витрувия, Лоренцо Гиберти, Леона Батиста Альберти, Пьеро дела Франческа, Леонардо да Винчи, Альбрехта Дюрера.

Исключительные заслуги в области начертательной геометрии принадлежат французскому инженеру и крупному ученому, прогрессивному общественному деятелю Гаспару Монжу (1746—1818), которого по праву называют творцом начертательной геометрии. Гаспар Монж так определял две главные цели этой науки: «Первая — точное представление на чертеже, имеющем только два измерения, объектов трехмерных, которые могут быть точно заданы… Вторая цель начертательной геометрии — выводить из точного описания тел все, что неизбежно следует из их формы и взаимного расположения. В этом смысле — это средство искать истину…».

В разделе «Начертательная геометрия» рассматриваются темы по методам проецирования, понятие комплексного чертежа, позиционные и метрические задачи, вопросы проецирования точки, прямой и плоскости, построение многогранников и тел вращения, линии пересечения плоскостей и объемных тел, аксонометрические проекции. Данный раздел состоит в основном из лекционного материала, который подкрепляется выполнением практических примеров по всем темам раздела. Практические примеры выполняются как в часы аудиторных занятий, так и самостоятельно с последующей проверкой преподавателем.

Методы проецирования

Центральное и параллельное проецирование.В начертательной геометрии прежде всего следует усвоить некоторые термины: плоскость проекций — та плоскость, на которой строится изображение предмета; проекция — изображение предмета на плоскости, полученное с помощью прямых линий, проведенных через множество точек на поверхности предмета до пересечения их с плоскостью проекций; проецирование — процесс образования проекций; проецирующая прямая (или луч) — прямая, проведенная через точку на поверхности предмета по заданному направлению до пересечения с плоскостью проекций.

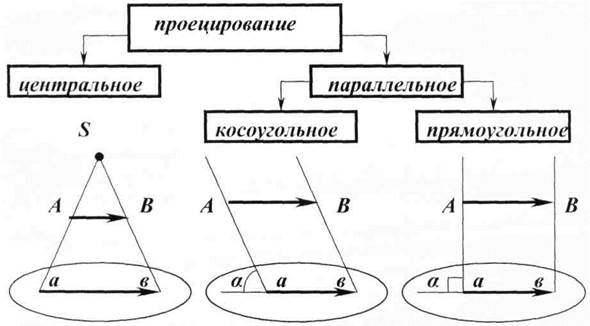Проецирование называется центральным, если проецирующие лучи выходят из одной точки (например, центра S — рис. 1).

Рис. 1. Методы проецирования

Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным, а полученные изображения — параллельной проекцией. Направление проецирования задается вектором, параллельно которому проводят проецирующие лучи. Если проецирующие лучи проводятся к плоскости проекций под углом, отличным от прямого, то проецирование называется параллельным косоугольным, полученная проекция будет косоугольной. В том случае, когда проецирующие прямые идут к плоскости проекций под прямым углом, то проецирование называется параллельным прямоугольным и проекция будет прямоугольной. Метод прямоугольного (ортогонального) проецирования наиболее прост и удобен, чертежи чаще всего делаются в прямоугольных проекциях.

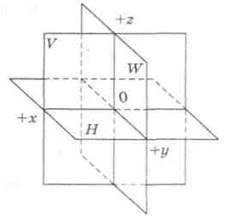
Пространственная модель координатных плоскостей проекций.Пересечением двух плоскостей пространство делится на 4 части, называемые четвертями (рис. 2, а).

а б

Рис. 2. Пространственная модель координатных плоскостей

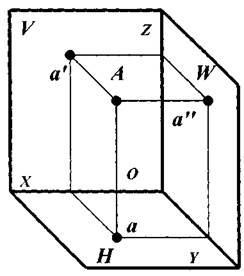
Горизонтальная плоскость проекций — горизонтальная плоскость, на которой располагается наблюдатель (Н). Фронтальная плоскость проекций — вертикальная плоскость перед наблюдателем (V). Первой четвертью I считается часть пространства, где обе плоскости проекций видимы наблюдателю. Профильная плоскость проекций (W) — вертикальная плоскость, находящаяся справа от наблюдателя. Плоскости H, V, W делят пространство на 8 частей, называемых октантами. Обычно пользуются первым октантом, где координаты по осям имеют положительное значение (рис. 2, б).

Проецирование точки и прямой.Прямоугольная проекция точки — это основание перпендикуляра, опущенного из точки на плоскость проекций. Проекция точки на плоскость H называется горизонтальной проекцией точки (а); на плоскость V — фронтальной проекцией точки (а^'); на плоскость W — профильной проекцией точки (а^'') — рис. 3, а.

Для построения проекций прямой линии достаточно построить проекции ее концевых точек. Прямая линия на плоскостях проекций может быть задана двумя способами:

– проекциями двух точек, принадлежащих прямой;

– проекциями отрезка прямой.

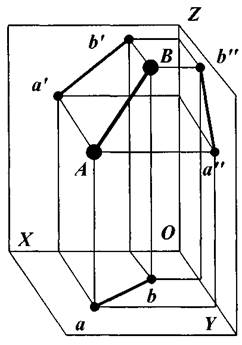
На рис. 3, б показаны проекции прямой АВ на горизонтальную плоскость проекций (ab); на фронтальную плоскость проекций (a^'b^'); на профильную плоскость проекций (a^''b^'').

Проекции и точки и прямой определяются проецирующими линиями (проецирующими лучами), проведенными из соответствующих точек на плоскости проекций.

а б

Рис. 3. Проецирование точки и прямой линии на плоскости проекций

Комплексный чертеж

Комплексный чертеж(эпюр Монжа) — чертеж, который для первого октанта получен совмещением горизонтальной и профильной плоскости проекций при их повороте на 90⁰ относительно осей проекций (рис. 4).

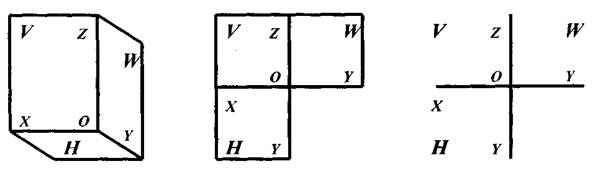Рис. 4. Образование комплексного чертежа

Линией проекционной связи называют прямую, расположенную перпендикулярно оси проекций и соединяющую две проекции точки (a¢a; a¢a ¢¢; aa¢¢) — рис. 5. Фронтальная и горизонтальная проекции точек располагаются на вертикальной линии проекционной связи (a¢a), а фронтальная и профильная проекции точки — на горизонтальной линии проекционной связи (a¢a¢¢).

Вспомогательная прямая (ВП) проводится из начала координат (точка 0) под углом 45^° для переноса координат по оси y (рис. 5).

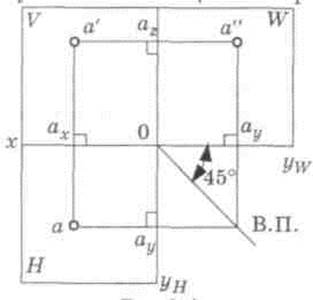Рис. 5. Проекции точки на комплексном чертеже

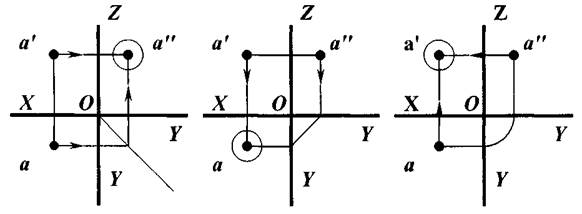
Зная две проекции точки А на плоскости проекций, можно построить ее третью проекцию одним из трех способов, показанных на рис. 6. Положение неизвестных проекций можно определить:

а) профильной проекции по фронтальной и горизонтальной проекциям;

б) горизонтальной проекции по фронтальной и профильной проекциям;

в) фронтальной проекции по горизонтальной и профильной проекциям.

а б в

Рис. 6. Построение третьей проекции точки

Эпюры и координаты точки. Положение точки в пространстве задают с помощью ее координат. Координатами точки называют расстояния от этой точки до плоскостей проекций, определяемые параллельно осям координат. Координаты обозначаются: a_x = Aa ¢¢; a_y = Aa^’; a_z = Aa (рис. 7).

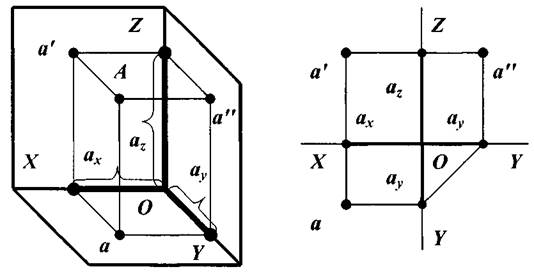Рис. 7. Координаты точки в пространстве и на комплексном чертеже

Позиционные задачи

Эпюры прямых линий. Так как положение прямой в пространстве определяется координатами двух ее точек, то для построения проекций прямой линии достаточно построить проекции ее концевых точек и соединить их отрезками прямой. Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения. Все проекции такой прямой располагаются под острыми углами к осям проекций (рис. 8).

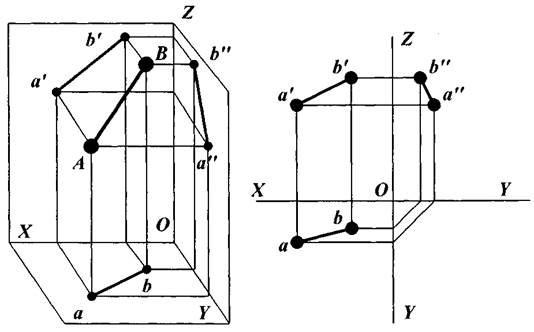Рис. 8. Прямая общего положения и ее проекции

Точки пересечения прямой с плоскостями проекций называются следами прямой. Прямые общего положения имеют три следа: горизонтальный, профильный и фронтальный (рис. 9).

Рис. 9. Следы прямой линии общего положения

Отношение длины проекции отрезка к действительной длине отрезка называется коэффициентом искажения. Значение коэффициента искажения численно равно косинусу угла наклона прямой к плоскости проекций.

Прямые частного положения — это прямые, параллельные или перпендикулярные плоскостям проекций.

Если прямые расположены параллельно одной из плоскостей проекций и под углом к остальным, то они называются прямыми уровня (рис. 10). Прямые уровня имеют два следа.

Горизонтальной прямой (или горизонталью) называется прямая, параллельная горизонтальной плоскости проекций. Ее фронтальная проекция a¢b^’ параллельна оси x, профильная проекция a¢¢b¢¢ параллельна оси y. На горизонтальную плоскость проекций горизонтальная прямая проецируется в действительную величину.

Фронтальной прямой (или фронталью) называется прямая, параллельная фронтальной плоскости проекций. Ее горизонтальная проекция ab параллельна оси x, а профильная проекция a¢¢b¢¢ параллельна оси z. На фронтальную плоскость проекций фронталь проецируется в натуральную величину.

Профильной прямой называется прямая, параллельная профильной плоскости проекций. Ее горизонтальная проекция ab параллельна оси y, а фронтальная проекция параллельна оси z (можно сказать, что обе проекции параллельны оси z). На профильную плоскость проекций профильная прямая проецируется в действительную величину.

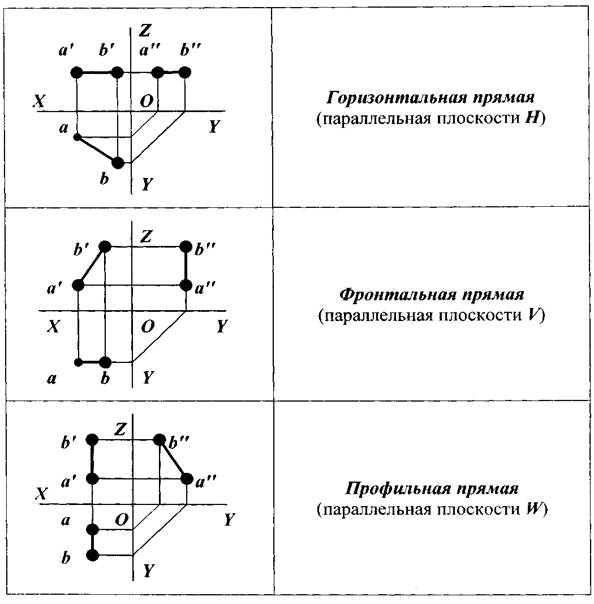
Рис. 10. Прямые уровня

Прямые, расположенные перпендикулярно одной из плоскостей проекций, а, следовательно, параллельно двум остальным, называются проецирующими прямыми (рис. 11). Все точки проецирующей прямой лежат на одном проецирующем луче. Проецирующие прямые имеют один след.

Горизонтально-проецирующая прямая перпендикулярна горизонтальной плоскости проекций и проецируется на нее в точку (a 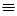b). Ее фронтальная и профильная проекции параллельны оси z и перпендикулярны осям x и y. На фронтальную и профильную плоскости проекций такая прямая проецируется в действительную величину.

Фронтально-проецирующая прямая перпендикулярна фронтальной плоскости проекций и проецируется на нее в точку (a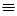^’ b^’). Ее горизонтальная ab и профильная a^”b^” проекции параллельны осям z и x и на горизонтальную и профильную плоскости проекций проецируются в действительную величину.

Профильно-проецирующая прямая перпендикулярна профильной плоскости проекций и проецируется на нее в точку (a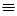^” b^”). Ее горизонтальная ab и фронтальная a^’b^’ проекции параллельны оси x и проецируются на горизонтальную и фронтальную плоскости проекций в натуральную величину.

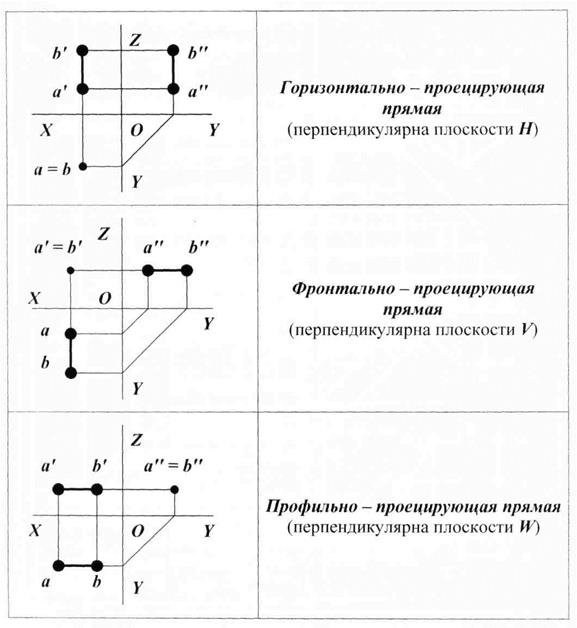
Рис. 11. Проецирующие прямые

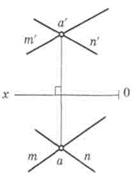
Если точка принадлежит прямой, лежащей в пространстве, то все проекции точки лежат на соответствующих проекциях прямой.

Все проекции параллельных прямых располагаются параллельно друг другу (рис. 12).

Если прямые линии пересекаются в пространстве, то все их проекции тоже пересекаются. При этом точки пересечения проекций лежат на одних линиях проекционной связи (a^’a), расположенных перпендикулярно осям проекций (рис. 13).

Для скрещивающихся прямых точка пересечения не лежит на одной линии проекционной связи. Видимой будет точка, расположенная дальше от плоскости проекций (рис. 14). Точки, лежащие на одном проекционном луче, называются конкурирующими. Невидимая точка обозначается (b).

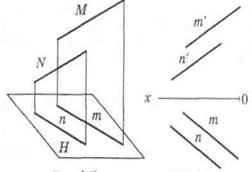Рис. 12. Проекции параллельных Рис. 13. Проекции

прямых пересекающихся прямых

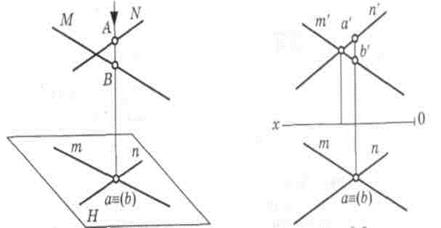Рис. 14. Проекции скрещивающихся прямых

Прямая, принадлежащая плоскости.Прямая принадлежит плоскости, если проекции прямой проходят через проекции двух точек, принадлежащих плоскости.

Пусть плоскость задана ABC и прямая задана отрезком MN (рис. 15).

1. ABC задан на комплексном чертеже горизонтальной проекцией abc и фронтальной проекцией a’b’c’.

2. Прямая MN задана горизонтальной проекцией (mn) и фронтальной проекцией (m’n’).

3. Проведем через MN вспомогательную фронтально-проецирующую плоскость P: P_V — фронтальный след плоскости.

4. Отметим следы P_X и P_H.

5. Отметим фронтальные проекции точек пересечения плоскости P и плоскости ABC: 1’, 2’на прямых (a’b’) и (a’c’).

6. Найдем горизонтальную проекцию 1, 2 проекционными лучами на прямых (ab) и (ac).

7. Соединим 1 и 2, получим прямую (12).

8. Так как (mn) лежит на прямой (12), то прямая MN принадлежит плоскости ABC.

Pv

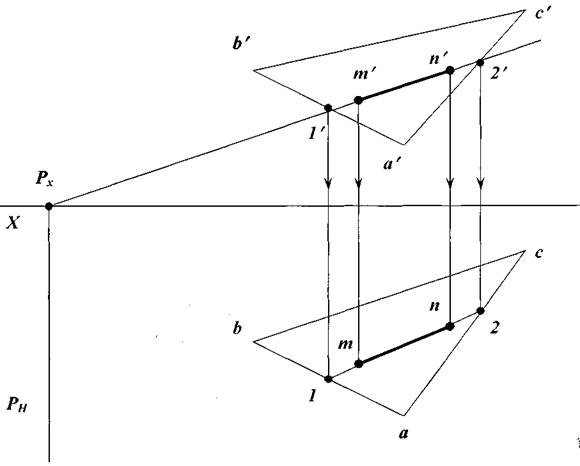
Рис. 15. Определение принадлежности прямой данной плоскости

Пересечение прямых линий с плоскостями.Если прямая пересекается с плоскостью, то для определения точки пересечения необходимо:

- через прямую провести проецирующую плоскость;

- построить линию пересечения проецирующей плоскости с заданной плоскостью;

- на пересечении линии пересечения плоскостей с прямой определить точку пересечения прямой с плоскостью;

- методом конкурирующих точек определить видимость.

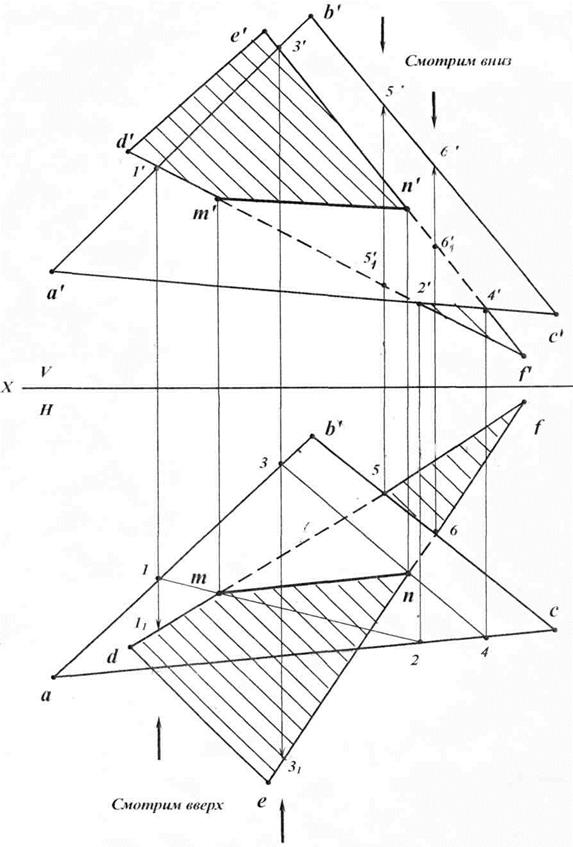
Плоскость задана ABC (рис. 16). Найти точку пересечения прямой MN с плоскостью треугольника и определить видимость проекций прямой MN.

1. Построение точки пересечения прямой MN с ABC.

Через MN проведем вспомогательную фронтально-проецирующую плоскость P: P_V — след фронтально-проецирующей плоскости.

Отметим следы P_X и P_H.

Отметим фронтальные проекции точек пересечения плоскости P и ABC: e’, d’.

Найдем горизонтальные проекции e, d линиями проекционной связи.

Проведем прямую (ed).

(ed) 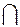(mn) = k — это точка пересечения.

Pv

Найдем фронтальную проекцию k’ проекционными лучами на прямой (m’n’).

Рис. 16. Пересечение прямой и плоскости

2. Определение видимости проекций прямой MN
методом конкурирующих точек

От e’ вниз на H проведена линия проекционной связи, найдем ее пересечения с прямыми (mn) и (ac): получаем горизонтальную проекцию e₁ на прямой (mn) и e на стороне (ac).

Проецировали сверху вниз, на точки e₁ и e смотрим снизуи видим сначала точку e на abc, поэтому на фронтальной проекции треугольник закрывает прямую.

Рассмотрим точку f = (cb) (mn).

От точки f на V проведем проекционный луч и найдем его пересечение с прямой (m’n’) и стороной (c’b’): получаем фронтальные проекции f ’ на сторону (c’b’) и f₁’ на прямую (m’n’).

Проецировали снизу вверх, на точки f₁’ и f ’ смотрим сверхуи видим сначала точку f₁’ на прямой (m’n’), следовательно, на горизонтальной проекции прямая закрывает треугольник.

Проецирование плоскости

Задание плоскости на эпюре. Плоскость на чертеже может быть задана:

1) проекциями трех точек, не лежащих на одной прямой;

2) проекциями прямой и точки, не лежащей на этой прямой;

3) проекциями двух параллельных прямых;

4) проекциями двух пересекающихся прямых;

5) проекциями плоской фигуры;

6) следами.

Плоскость в первом октанте задана двумя пересекающимися прямыми (рис. 17).

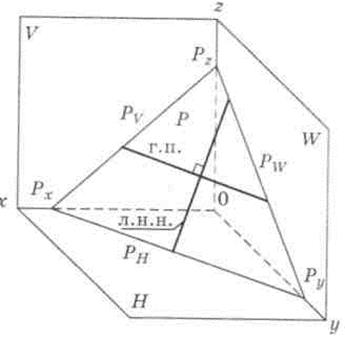Рис. 17. Задание плоскости на эпюре

Следом плоскости называется линия пересечения плоскости с плоскостями проекций (P_H, P_V, P_W). Линия пересечения плоскости с горизонтальной плоскостью проекций называется горизонтальным следом P_H, с фронтальной плоскостью проекций — фронтальным следом P_V, с профильной плоскостью проекций — профильным следом P_W.

Точками схода следов называются точки пересечения следов плоскости между собой P_x, P_y, P_z.

Главные линии плоскости: горизонталь плоскости — прямая, лежащая в плоскости параллельно горизонтальной плоскости проекций (отмечена на рис. 17 Г.П.); фронталь плоскости — прямая, лежащая в плоскости параллельно фронтальной плоскости проекций; профильная линия — прямая, лежащая в плоскости параллельно профильной плоскости проекций; линия наибольшего наклона (Л.Н.Н.) плоскости к плоскостям проекций — линия, лежащая в плоскости перпендикулярно линиям уровня или следам плоскости (в данном случае следу P_H).

Плоскостью общего положения называется плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций (рис. 17). Такие плоскости имеют три следа, расположенные под острым углом к осям проекций.

Плоскости частного положения расположены либо параллельно одной из плоскостей проекций (следовательно, перпендикулярно к двум остальным), либо перпендикулярно одной из плоскостей проекций.

Проецирующие плоскости перпендикулярны одной из плоскостей проекций (рис. 18).

а б в

Рис. 18. Эпюры проецирующих плоскостей

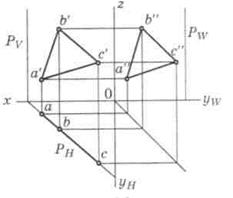
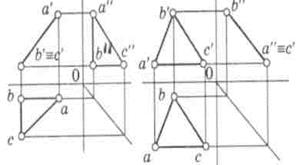
Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей. Плоская фигура (ΔABC) на горизонтальную плоскость проекций проецируется отрезком прямой линии, лежащим на горизонтальном следе P_H плоскости (рис. 18, а). На остальные плоскости проекций фигура проецируется с искажением. Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей. Она проецируется на плоскость V в виде отрезка прямой, а на плоскости H и W с искажениями (рис. 18, б). Плоскость, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей. Она проецируется на плоскостьW в виде отрезка прямой, а на плоскости H и V с искажениями (рис. 18, в).

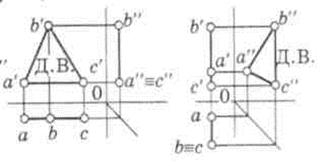
Плоскости уровня параллельны одной из плоскостей проекций (рис. 19).

а б в

Рис. 19. Эпюры плоскостей уровня

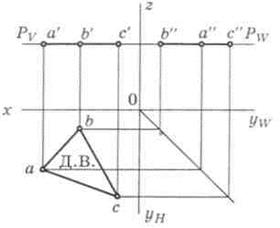
Плоскость, параллельная горизонтальной плоскости проекций, называется горизонтальной плоскостью. Фронтальный P_V и профильный P_W следы располагаются параллельно осям x и y_w (рис. 19, а). Плоская фигура проецируется на горизонтальную плоскость проекций в действительную величину (Д.В.). На две другие плоскости фигура проецируется в виде отрезков прямой, лежащих на соответствующих следах плоскости. Плоскость, параллельная фронтальной плоскости проекций, называется фронтальной плоскостью. На плоскость V она проецируется в действительную величину, а на остальные плоскости в виде отрезков прямой, параллельных осям x и z (рис. 19, б). Плоскость, параллельная профильной плоскости проекций, называется профильной плоскостью. На плоскость W она проецируется в действительную величину, а на остальные плоскости в виде отрезков прямых линий, параллельных оси y_H (рис. 19, в).

Взаимное пересечение плоскостей.Плоскости в пространстве могут быть либо параллельны, либо пересекаться одна с другой. Признаки параллельности двух плоскостей:

- плоскости параллельны, если соответствующие следы плоскостей параллельны друг другу;

- плоскости параллельны, если проекции двух пересекающихся прямых, принадлежащих одной плоскости, параллельны проекциям двух пересекающихся прямых, принадлежащих другой плоскости.

Если плоскости пересекаются, то для построения их линии пересечения необходимо:

1) определить точки пересечения двух прямых, принадлежащих одной плоскости, с другой плоскостью, или точку пересечения прямой, принадлежащей одной плоскости, с другой плоскостью и точку пересечения прямой, принадлежащей другой плоскости, с первой плоскостью;

2) через найденные точки провести прямую — это и будет линия пересечения;

Рис. 20. Пересечение плоскостей

3) определить видимость конкурирующих точек.

PH

PX

PV

Пример построений показан на рис. 20.

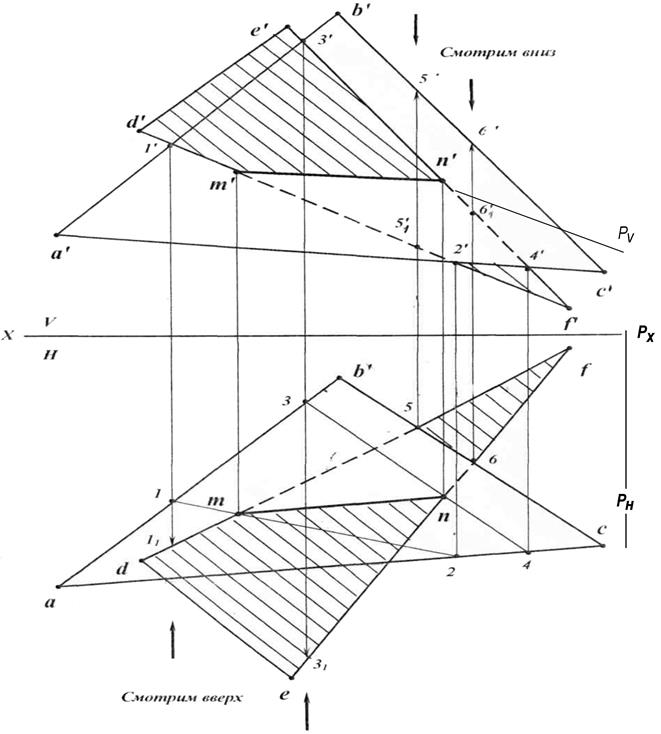
Рис. 20. Пересечение плоскостей

Определение линии пересечения плоскостей.

1. Построение точки M пересечения прямой DF с ABC.

1.1. Через прямую DF проведем вспомогательную фронтально-проецирующую плоскость P: P_V — фронтальный след.

1.2. Отметим следы P_X и P_H.

1.3. Отметим фронтальные проекции точек пересечения плоскости P и ABC: точки 1^’ и 2^’.

1.4. Найдем горизонтальные проекции — точки 1 и 2 проекционными лучами на прямых (ab) и (ac).

1.5. Проведем прямую (12).

1.6. (12) (df) = m.

1.7. Найдем фронтальную проекцию m’ на прямой (d’f ’).

2. Построение точки N пересечения прямой EF с ABC.

2.1. Через прямую EF проведем вспомогательную фронтально-проецирующую плоскость Q: Q_V — фронтальный след (на чертеже не показан).

2.2. Отметим следы Q_X и Q_H (на чертеже не показаны).

2.3. Отметим фронтальные проекции точек пересечения плоскости Q и ABC: точки 3’ и 4’.

2.4. Найдем горизонтальные проекции линиями проекционной связи — точки 3 и 4 на прямых (ab) и (ac).

2.5. Проведем прямую (34).

2.6. (34) (ef) = n.

2.7. Найдем фронтальную проекцию n’ на прямой (e’f ‘).

2.8. Соединим точки m’ и n’: (m’n’) — фронтальная проекция линии пересечения MN с ABC. Соединим точки m и n: (mn) — горизонтальная проекция линии пересечения MN с ABC.

Определение видимости проекций прямых EF и DF
методом конкурирующих точек.

1. Определение видимости проекций прямой DF.

1.1. От 1^’ = (d’f ’) (a’b’) вниз на H проведена линия проекционной связи, найдем ее пересечения с (ab) и (df): получим горизонтальные проекции: 1 на (ab), 1₁ на (df).

1.2. Проецировали сверху вниз, на 1 и 1₁ смотрим снизу и видим сначала точку1₁ на def, поэтому на фронтальной проекции d’e’f ‘ закрывает a’b’c’ от точки m’ до точки 1^’, тогда от точки m’ до точки 2^’ a’b’c’ закрывает d’e’f ‘.

1.3. От 5 = (df) (bc) вверх на V проведем линию проекционной связи и найдем ее пересечения с (b’c’) и (d’f ’): получим фронтальные проекции 5₁’ на (d’f ‘), 5’ на (b’c’).

1.4. Проецировали снизу вверх, на 5’ и 5₁’ смотрим сверхуи видим сначала точку 5’ на a’b’c’, поэтому на горизонтальной проекции abc закрывает def от точки m до точки 5, а от точки m до точки d def закрывает abc.

2. Определение видимости проекций прямой EF.

2.1. От 3’ = (e’f ’) (a’b’) вниз на H проведена линия проекционной связи, находим ее пересечения с (ab) и (ef): получаем горизонтальные проекции: 3 на (ab), 3₁ на (ef).

2.2. Проецировали сверху вниз, на 3 и 3₁ смотрим снизу и видим сначала точку 3₁ на def, поэтому на фронтальной проекции d’e’f ‘ закрывает a’b’c’ от точки n’ до точки 3’, тогда от точки n’ до точки 4’ a’b’c’ закрывает d’e’f ‘.

2.3. От 6 =(ef) (bc) вверх на V проведем линию проекционной связи и найдем ее пересечения с (b’c’) и (e’f ‘): получим фронтальные проекции: 6₁^’ на (e’f ‘),6^’ на (b’c’).

2.4. Проецировали снизу вверх, на 6^’ и 6₁^’ смотрим сверху и видим сначала точку 6^’ на a’b’c’, поэтому на горизонтальной проекции abc закрывает def от точки n до точки 6, тогда от точки n до точки e def закрывает abc.

Метрические задачи

Положение точки относительно плоскостей проекций.Точка принадлежит плоскости, если проекции точки лежат на соответствующих проекциях прямой, принадлежащих данной плоскости. Если точка лежит в плоскости проекций, то ее проекция на эту плоскость совпадает с самой точкой, а две другие проекции располагаются на осях проекций (рис. 21).

с

Две проекции точки, лежащие на оси проекций, совпадают с самой точкой, а третья находится в начале координат.

с