Прямоугольная изометрическая проекция.
В прямоугольной изометрии аксонометрические оси OX, OY, OZ расположены под углами 1200 одна к другой. Треугольник штриховок для прямоугольной изометрии приведен на рис. 79. Ось OZ вертикальна. Оси OX и OY удобно строить, откладывая с помощью угольника от горизонтали углы 300. Положение осей можно также определить, отложив от начала координат в обе стороны по пять произвольных равных единиц. Через пятые деления проводят вниз вертикальные линии и откладывают на них по 3 такие же единицы. Действительные коэффициенты искажения по осям равны 0,82. Чтобы упростить построение, применяют приведённый коэффициент, равный 1. В этом случае при построении аксонометрических изображений измерения предметов, параллельные направлениям аксонометрических осей, откладывают без сокращений.
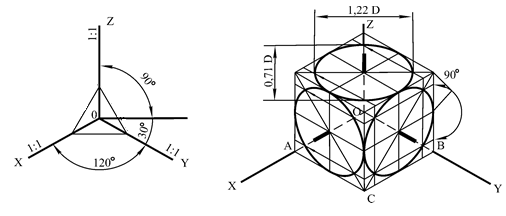
Рис. 79
Построение аксонометрических проекций предмета осуществляется по характерным точкам, дугам и окружностям.
Для построения аксонометрической проекции точки (рис. 80) требуется определить длины звеньев ее аксонометрической координатной ломаной. Для изометрической проекции длины звеньев этой ломаной равны длинам соответствующих звеньев натуральной координатной ломаной. Длины звеньев, параллельных осям ОХ, OY и OZ аксонометрической координатной ломаной для точки берутся равными длинам соответствующих звеньев натуральной ломаной (xA, yA, zA).
Окружности в прямоугольной изометрии изображаются в виде овалов ориентированных относительно осей. Расположение аксонометрических осей и построение прямоугольной изометрии куба, в видимые грани которого вписаны окружности, показаны на рис. 81.
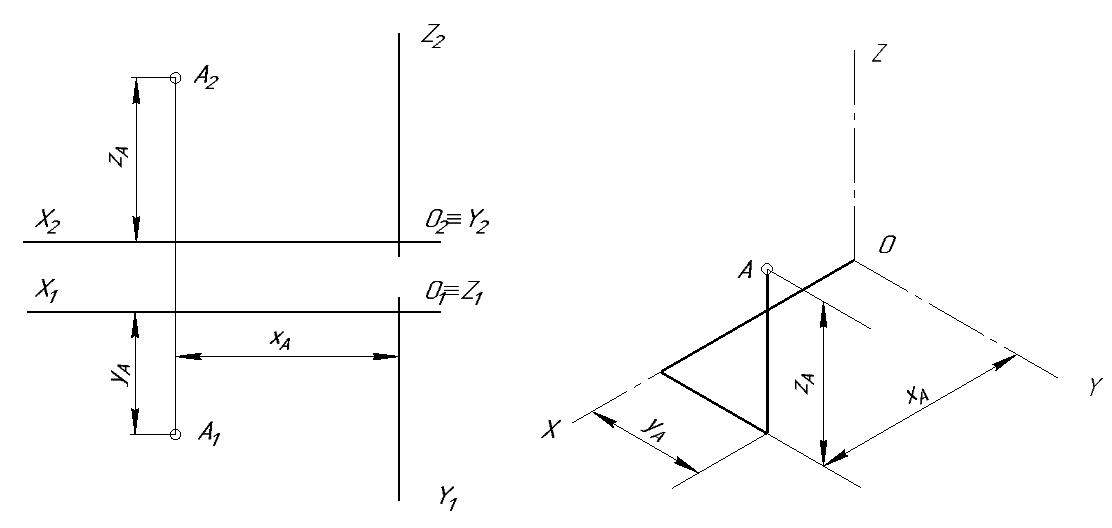
Рис. 80

Рис. 81
Окружности, вписанные в прямоугольную изометрию квадратов – трех видимых граней куба, – представляют собой эллипсы. Большая ось эллипса равна 1,22 D, а малая – 0,71 D, где D – диаметр изображаемой окружности. Большие оси эллипсов перпендикулярны соответствующим аксонометрическим осям, а малые оси совпадают с этими осями и с направлением, перпендикулярным плоскости грани куба (на рис. 81 – утолщенные штрихи).
При построении прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна той координатной оси, которая отсутствует в плоскости окружности, т.е. располагается параллельно линии штриховки в плоскости которой лежит окружность (см рис. 79 81).
Зная размеры осей эллипса и проекции диаметров, параллельных координатным осям, можно построить эллипс по всем точкам, соединяя их с помощью лекала.
Чтобы упростить построения, рекомендуется заменять эллипсы овалами, оси которых равны осям эллипса.
Построение овала по четырем точкам – концам сопряжённых диаметров эллипса, расположенных на аксонометрических осях, показано на рис. 82.
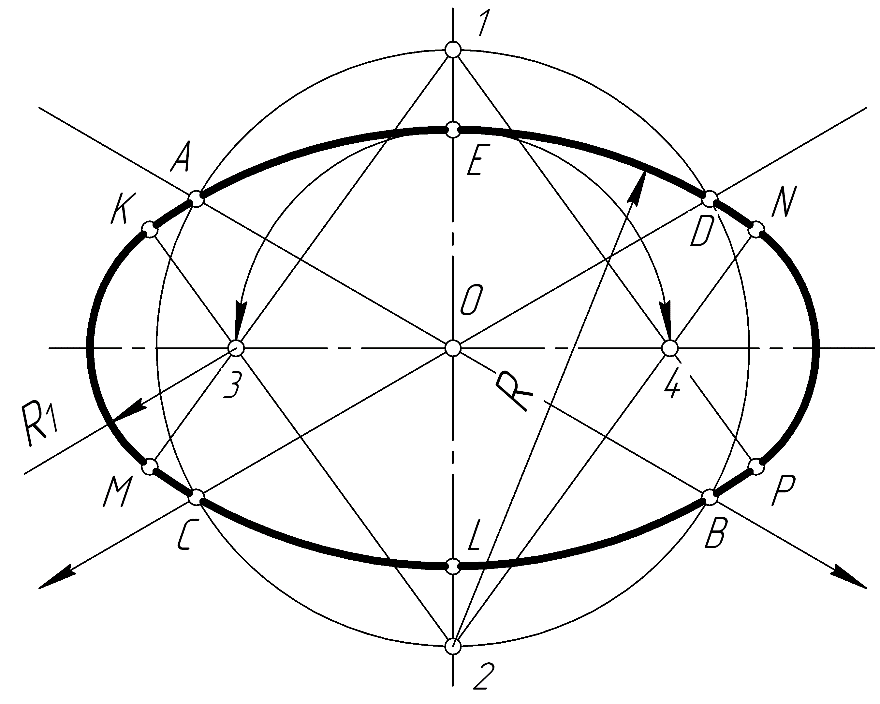
Рис. 82
Через точку О пересечения сопряжённых диаметров эллипса проводят горизонтальную и вертикальную прямые и из неё описывают окружность радиусом, равным половине сопряжённых диаметров АВ=СД. Эта окружность пересечёт вертикальную линию в точках 1 и 2 (центры двух дуг). Из точек 1, 2 проводят дуги окружностей радиусом R=2-А (2-D) или R=1-C (1-B). Радиусом ОЕ делают засечки на горизонтальной прямой и получают еще два центра сопрягаемых дуг 3 и 4. Далее соединяют центры 1 и 2 с центрами 3 и 4 линиями, которые в пересечении с дугами радиусом R дают точки сопряжений K, N, P, M. Крайние дуги проводят из центров 3 и 4 радиусом R1=3-М (4-N).
