Задачи – «Прямая на эпюре Монжа»

Варианты исходных данных для задач по теме «Прямая на эпюре Монжа» приведены в табл. 3.

Задача 1. Построить прямую l, проходящею через точки А и В. На прямой l определить положение точки D если известно, что она удалена от плоскости проекций π₁ или π₂ на расстояние k.

Пример (рис. 22). Построить прямую l проходящею через точки А(20; 10;50) и В(60;70;20). На прямой l определить положение точки D если известно, что она удалена от плоскости проекций π₁ на расстояние 35 мм.

Задача 2. Через точку А провести фронталь f под углом 45⁰ к плоскости π₁. На фронтале найти одно из двух возможных положение точки Е если известно, что отрезок[AE]=30 мм.

На рис. 23 показан пример решения задачи для точки А(20; 10;50).

Задача 3. Через точку В провести горизонталь h под углом 60⁰ к плоскости π₂. На горизонтали найти одно из двух возможных положение точки F если известно, что отрезок[BF]=35 мм.

На рис. 24 показан пример решения задачи для точки В(60;70;20).

Задача 4. Через точку С провести профильную прямую p под углом 30⁰ к плоскости π₂. На профильной прямой найти одно из двух возможных положение точки К если известно, что отрезок[СК]=30 мм.

На рис. 25 показан пример решения задачи для точки С(40;25;35).

Задача 5. Через точки А, В, и С провести соответственно горизонтально-проецирующею (n), фронтально-проецирующею (m) и профильно-проецирующею (l) прямые.

На рис. 26 показан пример решения задачи для точек А(20; 10;50), В(60;70;20) и С(40;25;35).

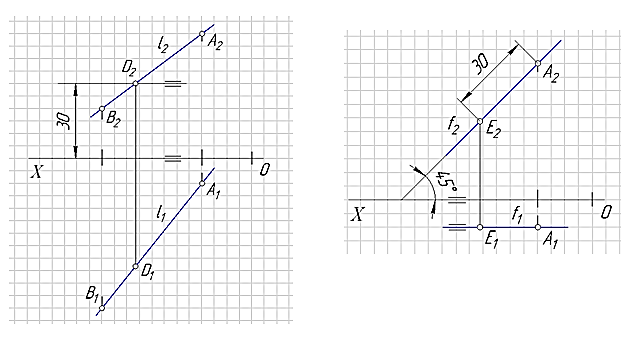
Рис. 22 Рис. 23

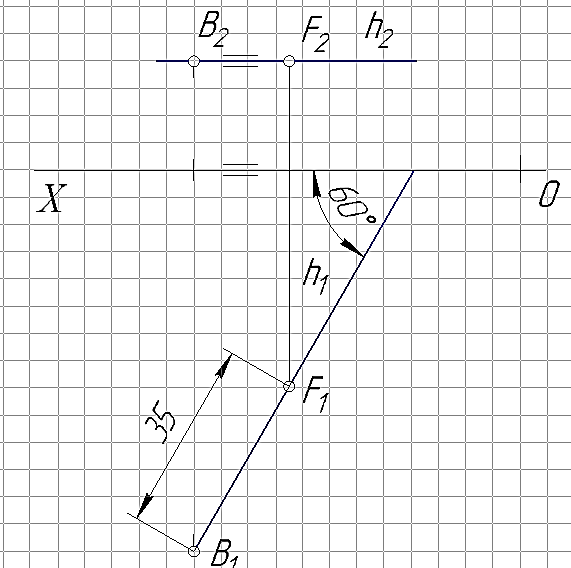
Рис. 24

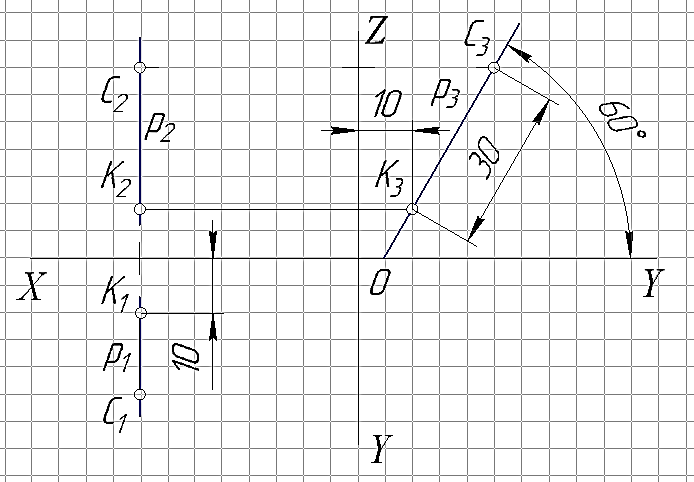
Рис. 25

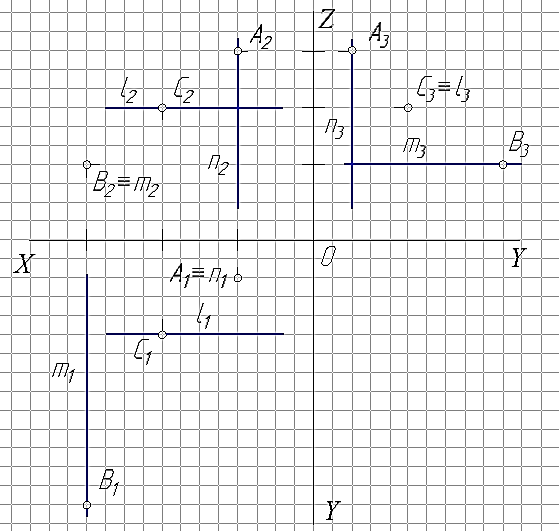
Рис. 26

Задача 6. С прямой l, преходящей через точки А и С пересекается прямая u параллельная плоскости π₁ или π₂ (согласно задания) и проходящая через точку L.

На рис. 27 показан пример решения задачи для точек А(20; 10;50), С(40;25;35), .L(5;20;10) ипрямой u параллельной плоскости π₂.

Задача 7. Через точку Т провести прямую l параллельную прямой m, проходящей через точки А и В.

На рис. 28 показан пример решения задачи для точек А(20; 10;50), В(60;70;20) и Т(20;40;20).

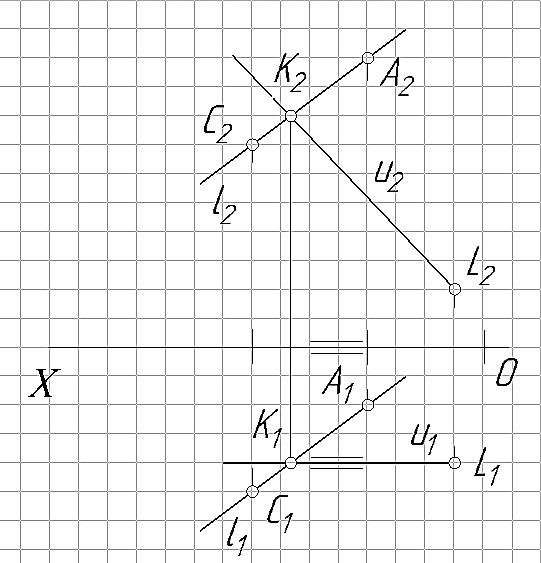
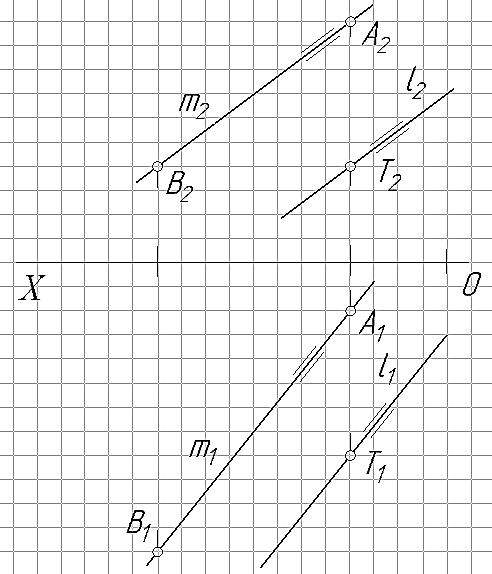
Рис. 27 Рис. 28

Таблица 3

Исходные данные по теме «Прямая на эпюре Монжа»

Вариант

Удаление точки D

Численные значения координат точек

Прямая u параллельна плоскости проекций

А

В

С

T

L

от

v

x

y

z

x

y

z

x

y

z

x

y

z

x

y

z

π1

π1

π2

π2

π1

π1

π2

π2

π1

π1

π2

π2

π1

π1

π2

π2

π1

π1

π2

π2

π1

π1

π2

π2

π1

π1

π2

π2

ПЛОСКОСТЬ

Задание плоскости на эпюре Монжа

Плоскость на эпюре может быть задана: тремя точками А, В и С (рис. 29а); точкой А и прямой l (рис. 29б); двумя пересекающимися прямыми l и k (рис. 29в); двумя параллельными прямыми l и k (рис. 29г); плоской фигурой - ∆АВС (рис. 29г).

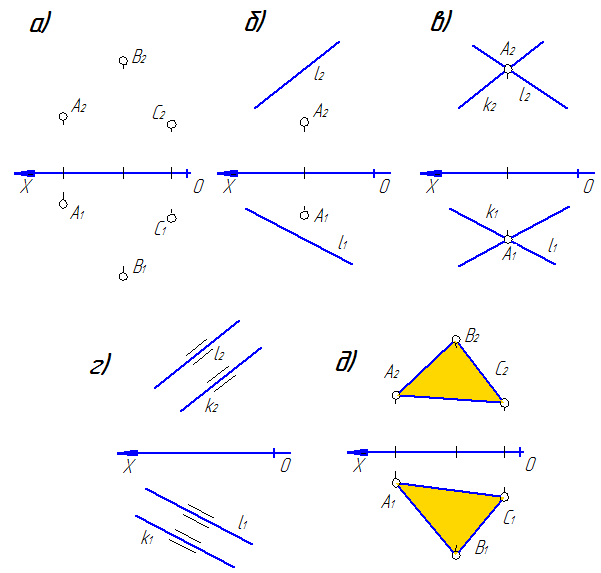
Рис. 25

Задачи по теме – «Задание плоскости на эпюре Монжа»

Используя точки А, В и С на эпюре Монжа задать плоскость α: тремя точками; точкой и прямой; двумя пересекающимися прямыми; двумя параллельными прямыми; плоской фигурой.

Варианты заданий приведены в табл. 4.

Пример решения задачи приведен на рис. 26, … , рис. 30 для точек А(70;10;5), В(50;40;40) и С(20;20;25)

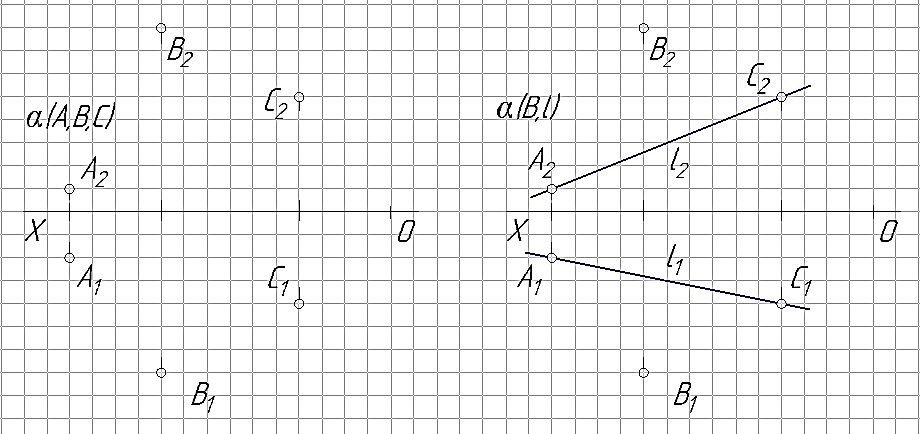
Рис. 26 Рис. 27

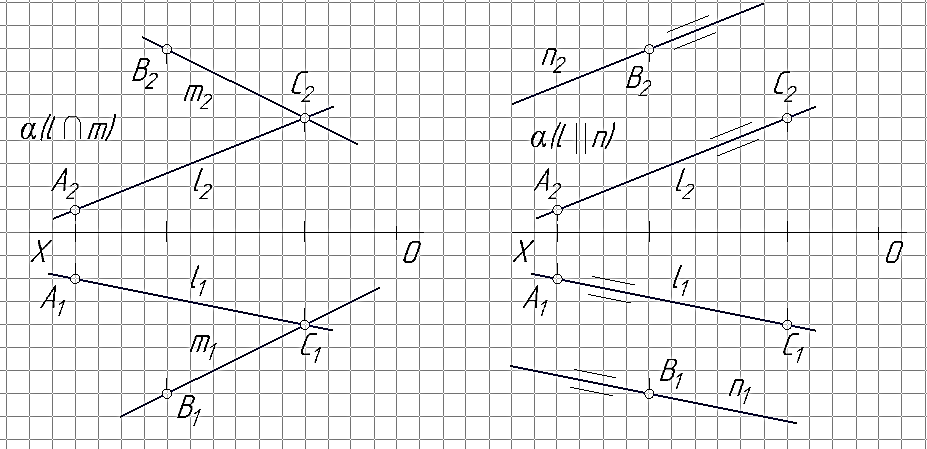
Рис. 28 Рис.29

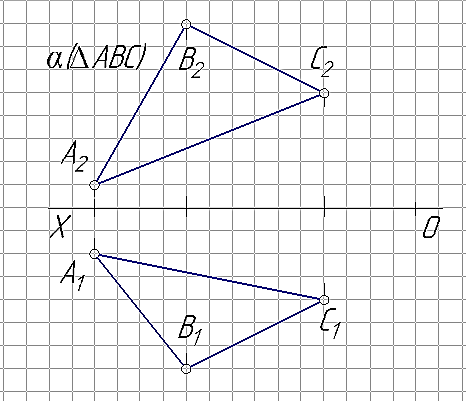
Рис. 30

Таблица 4

Исходные данные по теме «Задание плоскости на эпюре Монжа»

Вариант	Численные значения координат точек
А	В	С
x	y	z	x	y	z	x	y	z

ПОЗИЦИОННЫЕ ЗАДАЧИ