Развертка конической поверхности общего вида

Рассмотрим развертку конической поверхности на примере построения развертки наклонного конуса (рис. 69).

Для получения развертки боковой поверхности наклонного конуса в него вписывают многогранную пирамиду. Следует отметить, что чем больше граней у вспомогательной пирамиды, тем точнее развертка.

Примечание. Рекомендуется окружность основания конуса делить на 12 равных частей при R>25 мм и на 8 – при R<25 мм (R – радиус круга основания конуса).

Развертывание конической поверхности общего вида производится по схеме развертывания боковой поверхности наклонной пирамиды (см. п.10.2). На рис. 102, чтобы не затенять ход решения, в конус вписывается шестигранная пирамида с правильным шестиугольником в основании. Определение натуральных величин боковых ребер S2 и S3 осуществляется способом вращения вокруг оси i перпендикулярной плоскости π₁. Боковые ребра S1 и S4 на π₂ проецируются без искажения так как они являются фронталями, а основание на π₁ так как оно является горизонтальной плоскостью уровня.

Отличительной особенностью при построении является то, что полученные точки боковой поверхности, описывающие окружность основания конуса, соединяются не прямыми, а кривой с помощью лекало.

Основание конуса на развертке изображается кругом (в натуральную величину), касающимся в любой точке кривой боковой поверхности, описывающей основание.

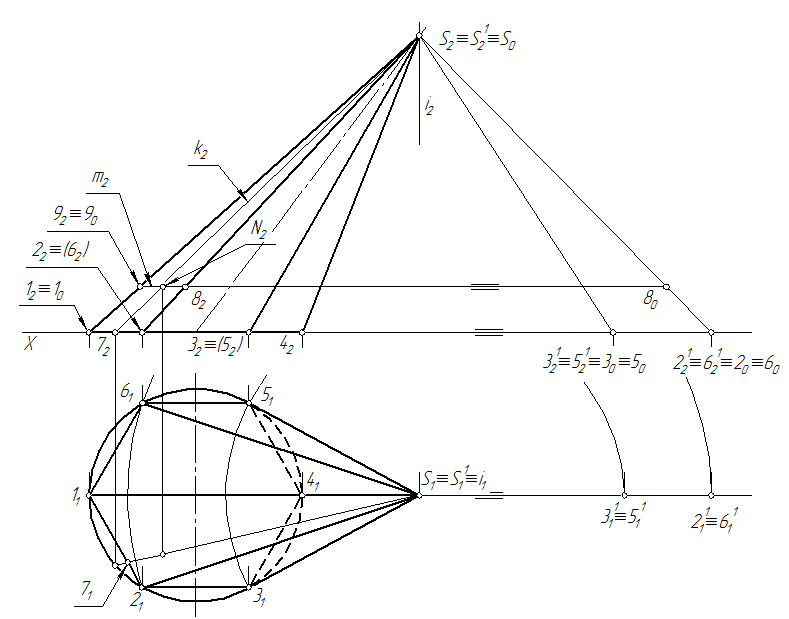
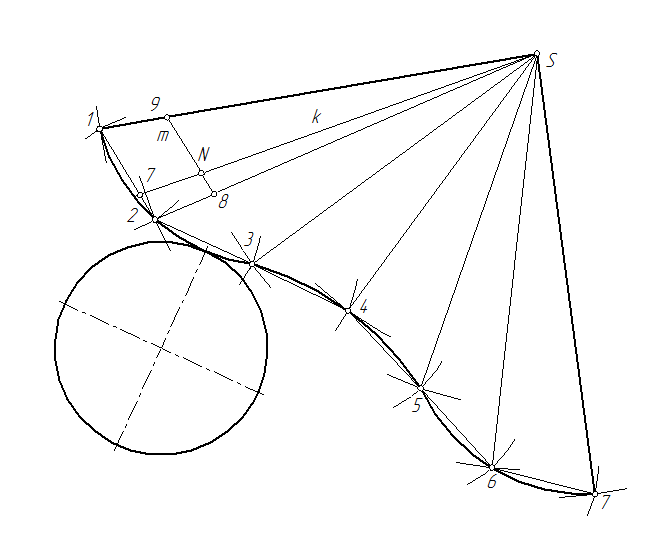
Рис. 69

Нанесение линии на развертку производится по точкам. Количество точек зависит от сложности конфигурации линии. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁ и k₂, образующей k,проходящей через вершину S и данную точку. Затем прямую k наносят на развертку при условии, что [17]=[1₁7₁]. Далее, через точку N проводится вторая прямая m, параллельная плоскости π₁. Эта прямая пересекает ребра S1 и S2 соответственно в точках 9 и 8. Точка 9 на развертке определяется используя отрезок, а точка 8 – используя отрезок [2₀8₀]=[18]. Положение точки 8₀ на ребре S₀2₀ находится с использованием теоремы Фалеса. Точка N на развертке определяется пересечением прямых k и m.

Развертка наклонного цилиндра

Чтобы построить развертку цилиндра, необходимо вписать в него призму с достаточно большим числом граней и развернуть ее. Чем больше граней у вспомогательной призмы, тем точнее развертка.

Примечание. Рекомендуется окружность основания цилиндра делить на 12 равных частей при R>25 мм и на 8 – при R<25 мм (R – радиус основания цилиндра).

Развертывание цилиндрической поверхности общего вида производится по схеме развертывания боковой поверхности наклонной призмы. Отличительной особенностью является то, что полученные точки боковой поверхности, описывающие окружности оснований цилиндра, соединяются не прямыми, а кривыми линиями с помощью лекал.

Основания цилиндра на развертке изображаются окружностями (в натуральную величину каждое), которые касаются в любой точке кривой боковой поверхности, описывающей это основание.

Методика построения линии пересечения поверхностей на развертке наклонного цилиндра аналогична методике, используемой при развертке призмы.

Частные случаи разверток

К частным случаям разверток относятся развертки прямого кругового конуса и прямого кругового цилиндра.

Развертка прямого кругового конуса.Развертка прямого кругового конуса (рис. 70) представляет собой сектор круга, радиус которого равен длине образующей конуса b, а центральный угол а

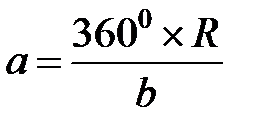, (1)

где R – радиус основания конуса.

Нанесение линии на развертку производится по точкам с использованием лекал. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k₁и k₂ образующей k, которой принадлежит эта точка. Затем прямую k наносят на развертку при условии, что длина дуги A₀K₀ равна длине дуги A₁K₁. Далее, используя теорему Фалеса, определяют истинное положение точки N₀: ([K₀N₀] =m).

Примечание. Развертку прямого конуса можно строить как развертку конической поверхности общего вида, т.е. в конус необходимо вписать правильную многогранную пирамиду.

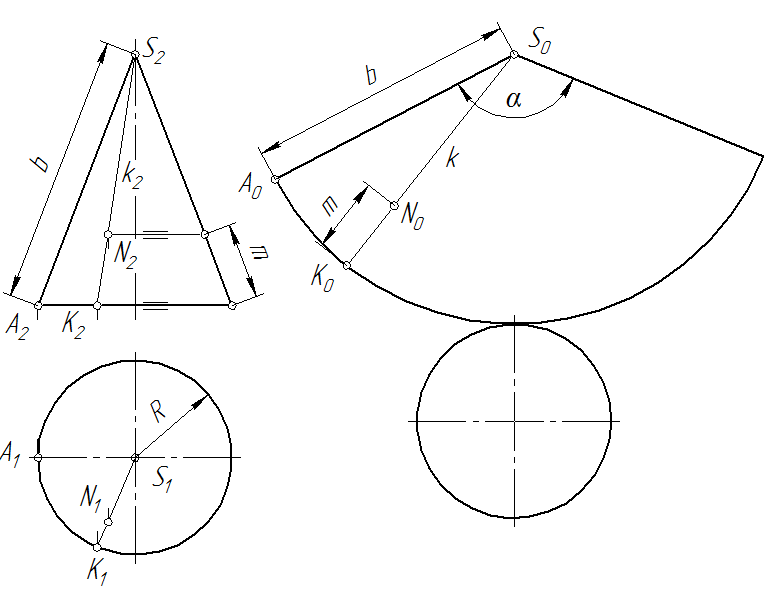
Рис. 70

Методика построения линии пересечения поверхностей на развертке конуса аналогична методике, используемой при развертке пирамиды.

Развертка прямого цилиндра.Развертка боковой поверхности прямого цилиндра представляет собой прямоугольник (рис. 71), одна сторона которого равна образующей l, а другая – длине окружности основания n:

n=2πR, (2)

где R – радиус основания окружности.

Каждое основание цилиндра наносят в виде круга с радиусом R,ка­сающегося в любой точке стороны п прямоугольника, описывающего его.

Нанесение линии пересечения поверхностей на развертку производится по точкам с использованием лекал. Положение любой точки поверхности на развертке, например N, определяется следующим образом. Вначале находят проекции k₁ и k₂ образующей k, которой принадлежит точка N. Затем определяют положение этой образующей на развертке по условию, что отрезок [B₀K₀] равен длине дуги B₁K₁. Так как k₂=k, то положение точки N₀на развертке определяется как [N₀K₂]= [N₂K₂]

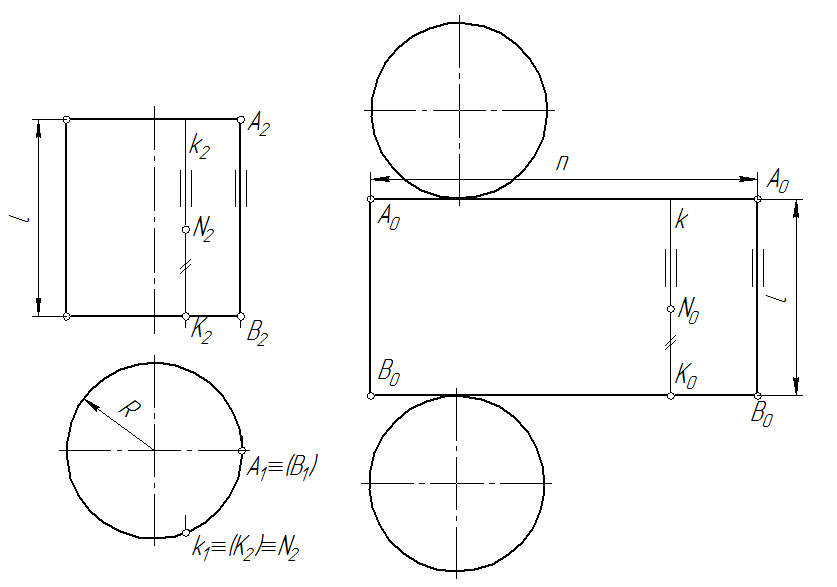
Рис. 71

Примечание. Развертку прямого цилиндра можно строить как развертку наклонного цилиндра, т.е. в цилиндр необходимо вписать правильную многогранную призму.

Развертка сферы

Сферическая поверхность является неразвертываемой. Здесь можно говорить только об условном развертывании. На рис. 72 показан один из приемов построения. Поверхность “разрезают” несколькими плоскостями, проходящими через ось сферы, перпендикулярную π₁. Точность развертки зависит от числа плоскостей – чем больше плоскостей, тем точнее развертка. На рис. 72 число таких плоскостей 12 (фронтальные проекции линий пересечения не показаны).

Дуги окружностей на плоскости π₁ в лепестках развертки заменяют прямыми, касательными к этим дугам, например, прямая А₁В₁ заменяет дугу ав.

На плоскости π₂ дугу 1₂7₂делят на равные части: 1₂2₂=2₂3₂=...=6₂7₂ (чем больше частей – тем точнее развертка). Принимая точки 1₂ 2₂, 3₂,... за фронтальные проекции отрезков АВ, CD, EF,образующих лепестки развертки, строят их горизонтальные проекции A₁B₁,C₁D₁, E₁F₁,...

На прямой l откладывают отрезок A₀B₀= A₁B₁ и через его середину (точка 1₀) проводят перпендикуляр k. На этом перпендикуляре откладывают отрезки [1₀2₀]= 1₂2₂, [2₀3₀]= 2₂3₂, [3₀4₀]= 3₂4₂, [4₀5₀]= 4₂5₂, [5₂6₂]= 5₂6₂и[6₂7₂]= 6₂7₂и через полученные точки 2₀, 3₀, 4₀, 5₀,и6₀проводят отрезки [C₀D₀]=[C₁D₁]_, [E₀F₀]=[E₁F₁] и т.д., параллельные прямой A₀B₀, при этом точки 2₁≡2₀,3₁≡3₀ и т.д.

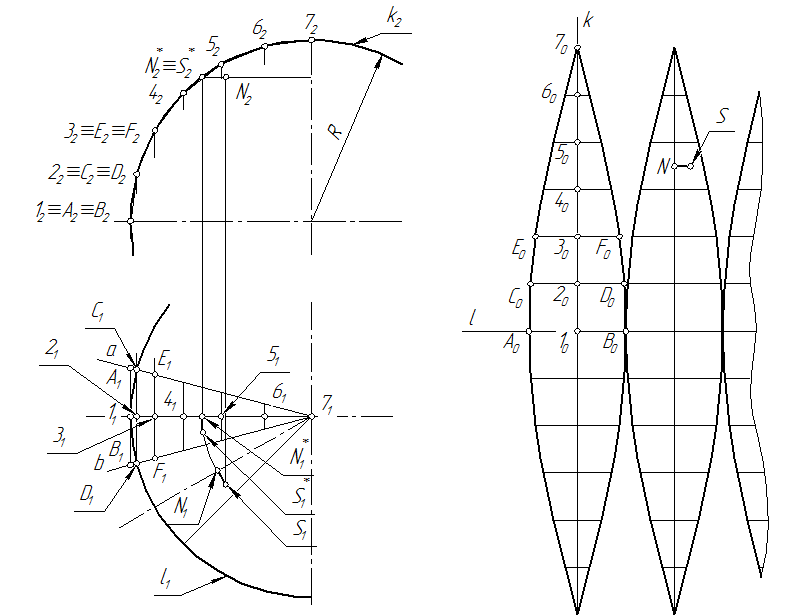
Рис. 72

По лекало через полученные точки А₀, D₀, F₀,...,7₀ и В₀ С₀, E₀…, 7₀ проводят кривые. В результате получается приближенная развертка половины лепестка сферической поверхности. Далее, используя эту часть лепестка, строят недостающую часть развертки.

Примечания.

1. Окружность сферы рекомендуется делить на 12 равных частей (лепестков) при R>25 мм и на 8 – при R<25 мм (R – радиус сферы).

2. Дугу 1₂7₂ следует делить не менее чем на 4 равные части (6, 8, 10 или 12 частей).

Построение линии пересечения поверхностей на развертке произво­дится по ее точкам с использованием лекал.

Для нахождения положения точки на развертке, например, S, опреде­ляют ее положение относительно экватора ( 1₂S*₂) и центральной линии сегмента [S₁N₁], в котором она находится. Далее полученные значения этих величин наносят на развертку, т.е. [1N]- 1₂S₂* и [SN]=[S₁N₁].

5.8. Контрольные вопросы

1. Что называется развёрткой поверхности?

2. Какие поверхности относятся к развёртывающимся поверхностям?

3. Можно ли построить развёртку неразвёртывающейся поверхности?

4. Каким способом строят развёртки пирамидальных (конических) поверхностей? В чём его сущность?

5. Как нанести на развёртку пирамидальной (конической) поверхности точку, ей принадлежащую?

6. Какую форму имеет развёртка поверхности прямого кругового конуса?

7. Каким способом сроят развёртки призматических (цилиндрических) поверхностей?

8. Как нанести на развёртку призматической (цилиндрической) поверхности точку, ей принадлежащую?

9. Что собой представляет развёртка поверхности прямого кругового цилиндра?

10. Каким способом строят развертку сферы?

11. Как нанести на развёртку сферы точку, ей принадлежащую?

ИНЖЕНЕРНАЯ ГРАФИКА

Лекция 6. СТАНДАРТЫ ЧЕРТЕЖА

1.1. Общие сведения о ГОСТ ЕСКД.

1.2. Виды чертежей.

1.3. Форматы, рамка, основная надпись.

1.4. Масштабы.

1.5. Линии чертежа.

1.6. Шрифты чертежные.

1.7. Графическое обозначение материалов и правила их нанесения на чертежах.

1.8. Нанесение размеров на чертежах.

1.9. Рекомендации по оформлению чертежа.

1.10. Контрольные вопросы.

Общие сведения о ГОСТ ЕСКД

Любые чертежи должны выполняться с соблюдением определенных графических условностей и правил. Это позволит обеспечить единство понимания чертежей и изготовление по ним требуемых изделий.

Эти условности сведены в Государственные стандарты. Соблюдение стандартов обязательно для всех.

Стандарт – нормативно-технический документ, устанавливающий комплекс норм, правил и требований к объекту стандартизации и утвержденный (принятый) компетентным органом.

Введенная в действие в 1971 году единая система конструкторской документации (ЕСКД) представляет собой комплекс стандартов, устанавливающих правила выполнения, оформления и обращения конструкторской документации, разрабатываемой и применяемой проектно-конструкторскими организациями и промышленными предприятиями.

Система стандартов унифицирует разработку всех видов конструкторской документации, ее учет, хранение, дублирование и внесение изменений, регламентирует все стадии разработки документации в производственных условиях.

Стандартами ЕСКД установлено деление всех изделий по видам для всей промышленности, определены общие для всех виды чертежей и одинаковая комплектность документов.

Стандарты ЕСКД отнесены ко второму классу и распределены по группам.

К конструкторским документам относят графические и текстовые документы (рабочие чертежи деталей, сборочные чертежи, общий вид, схемы, пояснительная записка).

Пример обозначения стандартов ЕСКД «Виды изделий» представлен на рис. 73.

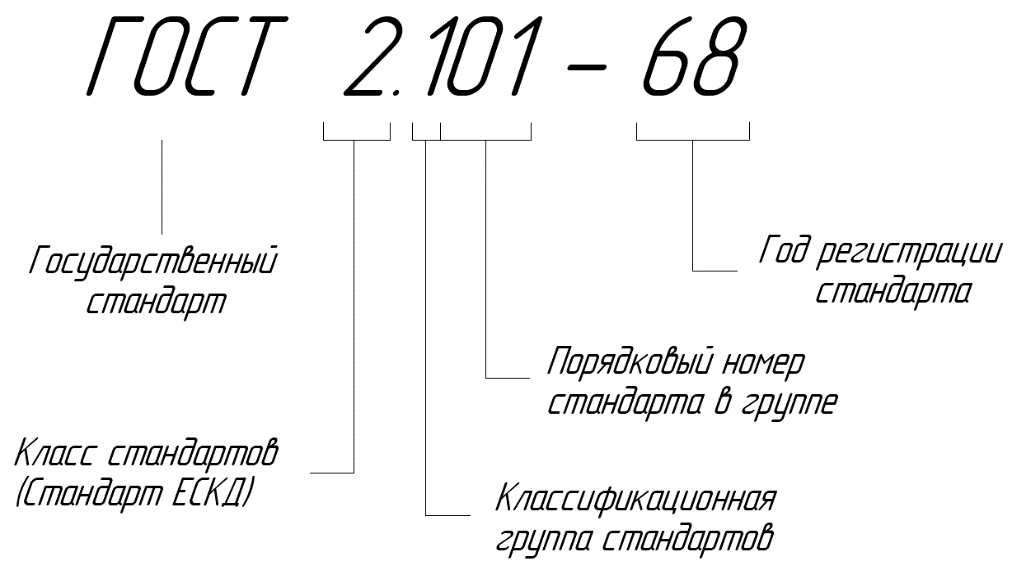
Рис. 73. Обозначение стандартов ЕСКД

Виды чертежей

Изготовление любых предметов (технические детали, изделия и пр.), строительство зданий и сооружений осуществляются с помощью конструкторских документов – графических и текстовых. К графическим документам относятся чертежи и схемы изделий, зданий и сооружений, а к текстовым – пояснительные записки, ведомости, спецификации, технические условия.

В соответствии с содержанием конструкторским документам согласно ГОСТ 2.102-68 присвоены следующие определения.

Чертеж детали – документ, содержащий изображение детали и все необходимые данные для ее изготовления и контроля.

Сборочный чертеж – документ, содержащий изображение сборочных единиц и необходимые данные для выполнения и контроля сборки.

Чертеж общего вида – документ, определяющий конструктивное устройство изделия, взаимодействие основных его частей и принципы работы изделия.

Монтажный чертеж – документ, содержащий упрощенное изображение изделия или его составных частей, а также необходимые данные для их монтажа и установки.

Схема – это документ, на котором показаны в виде условных изображений или обозначений составные части изделия и связи между ними.

Спецификация – документ, определяющий состав сборочной единицы, комплекса или комплекта.

Строительные чертежи в зависимости от вида изображаемых объектов называют:

– архитектурно-строительными (чертежи жилых, общественных и про­из­водственных зданий);

– инженерно-строительными (чертежи инженерных сооружений – мосты, дороги, туннели, эстакады, гидротехнические сооружения и др.);

– топографическими (чертежи земной поверхности, рельефа местности).

В зависимости от способа получения и характера использования чертежи подразделяют на следующие виды (ГОСТ 2.102-68):

– оригиналы-чертежи, выполненные на чертежной бумаге или другом материале и предназначенные для изготовления по ним подлин­ников;

– подлинники-чертежи, оформленные подписями и выполненные на специальном материале, позволяющем воспроизводить с них копии;

– копии-чертежи, выполненные способом, который обеспечивает их идентичность с подлинником и предназначенные для использования их в производстве и строительстве;

– эскизы-документы, предназначенные для разового использования.