Лекция 1. ВВЕДЕНИЕ В НАЧЕРТАТЕЛЬНУЮ ГЕОМЕТРИЮ. МЕТОД ПРОЕКЦИЙ. ТОЧКА НА ЭПЮРЕ МОНЖА
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
И ИНЖЕНЕРНАЯ ГРАФИКА
Курс лекций
Рекомендовано Редсоветом университета
качестве учебного пособия
для студентов, обучающихся по направлению подготовки 23.03.01
«Технология транспортных процессов»
Пенза 2017
УДК 514.18+744(07)
ББК 22.151.3+30.11я73
| Рецензенты: | доцент Л.В. Ремонтова (ПензГТУ); кандидат технических наук, доцент О.Л. Викторова (ПГУАС) |
| Поляков Л.Г. Начертательная геометрия и инженерная графика. Курс лекций по направлению подготовки 23.03.01 «Технология транспортных процессов» / Л.Г. Поляков. – Пенза: ПГУАС, 2017. – 194 с. |
Приведены необходимые сведения для построения плоских геометрических моделей трехмерных объектов. Рассмотрены наиболее распространенные методы построения таких моделей. Даны примеры решения основных позиционных задач и построения разверток. Приведены основные сведения о построении чертежей деталей и их аксонометрического изображения. Кроме того рассмотрены методики построения чертежей соединения деталей, составление эскизов деталей с натуры и деталирования сборочных чертежей.
Учебное пособие построено по разделам в виде лекций, согласованных с учебными программами и требованиями ГОСТов.
Учебное пособие подготовлено на кафедре «Начертательная геометрия и графика» и предназначено для студентов, обучающихся по направлению подготовки 23.03.01 «Технология транспортных процессов».
© Пензенский государственный университет
архитектуры и строительства, 2017
© Поляков Л.Г., 2017
ПРЕДИСЛОВИЕ
Курс «Начертательная геометрия и инженерная графика» является теоретической основой построения чертежей, которые представляют собой полные графические модели конкретных инженерных изделий. Данный курс состоит из раздела «Начертательная геометрия» и раздела «Инженерная графика»
Изучение начертательной геометрии сводится к развитию пространственного представления и воображения, конструктивно-геометрического мышления, способностей к анализу и синтезу пространственных форм и отношений изучения способов конструирования геометрических пространственных объектов, способов получения их чертежей на уровне графических моделей и умению решать на этих чертежах задачи, связанные с пространственными объектами и их зависимости.
Инженерная графика признана дать студентам умение и навыки для изложения технических идей с помощью чертежа, а также понимание по чертежу объектов машиностроения и принципа действия изображенного технического изделия.
Начертательная геометрия и инженерная графика – первая ступень обучения студентов, на которой изучаются основные правила выполнения и оформление конструкторской документации.
В соответствии с ФГОС 3+ при изучении курса «Начертательная геометрия и инженерная графика» у студентов по направлению подготовки 23.03.01 «Технология транспортных процессов» формируются следующие общепрофессиональные (ОПК) и профессиональные компетенции (ПК):
- способность применять систему фундаментальных знаний (математических, естественнонаучных, инженерных и экономических) для идентификации, формулирования и решения технических и технологических проблем в области технологии, организации, планирования и управления технической и коммерческой эксплуатацией транспортных систем (ОПК-3);
- способностью решать стандартные задачи профессиональной деятельности на основе информационной и библиографической культуры с применением информационно- коммуникационных технологий и с учетом основных требований информационной безопасности (ОПК-5).
Исходя из требований ОПК и ПК следует, что в результате изучения дисциплины на основе планируемых результатов обучения (показателей достижения заданного уровня освоения компетенции) студент обязан:
Знать:
- методы изображения пространственных объектов на плоскости; элементы геометрии деталей;
- алгоритмы решения геометрических задач с пространственными объектами;
- стандарты, используемые при работе с чертежами; методы изображения пространственных объектов на проекционном чертеже и в аксонометрии; крепежные элементы и правила их вычерчивания в соединениях деталей;
- порядок и методику составления эскизов деталей;
- последовательность чтения сборочных чертежей и их деталирование;
Уметь:
- выполнять и читать чертежей изделий на основе метода прямоугольного проецирования;
- применять способы решения задач геометрического характера по изображениям пространственных объектов на плоскости; создавать и вносить изменения в чертежи объектов проектирования;
- применять вышеуказанные методики при работе конструкторской и технической документацией с точки зрения ее графической части.
Владеть:
- навыками работы с технической и конструкторской документацией.
Знания, умения и навыки, приобретенные при изучении дисциплины, необходимы как при изучении общеинженерных и специальных дисциплин, так и в последующей профессиональной деятельности.
Курс лекций содержит краткий текстовой материал к каждой из 9 лекций. Для выполнения чертежей на лекциях студент должен иметь с собой следующие инструменты и принадлежности:
§ треугольники с делениями (один – с углами 45° и катетами 130-150 мм, второй– с углами 30° и 60° и с большим катетом 200.. 220 мм);
§ простые карандаши твердости М или ТМ;
§ цветные карандаши твердости М – чёрный, зелёный, красный, жёлтый и синий (допускается в место карандашей использовать шариковые ручки);
§ циркуль;
§ принадлежности для заточки карандашей;
§ резинку мягкую для стирания карандашных линий и штрих для замазки ошибок на эпюрах.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Понятие о проецировании
Мост между стереометрией и планиметрией осуществляется с помощью метода проекций, составляющего теоретическую основу начертательной геометрии. Метод обоснован французским учёным Гаспаром Монжем в 1795 г. в г. Париже.
Для реализации метода необходим аппарат проецирования и объекты проецирования. Введём следующие обозначения (рис. 2):
1) аппарат проецирования – это плоскость проекций p и центр проецирования S или направление проецирования s;
2) объект проецирования – точки А, В, С, ... какой-либо фигуры;
3) результат проецирования – проекции Аp, Вp, Сp, …
Каждую точку пространства проецируем из центра S на плоскость p, т.е. проводим проецирующий луч, например SA (рис. 2а). Пересечение проецирующего луча с плоскостью проекций p даёт проекцию точки, например Аp. В данном случае имеем центральноепроецирование.
Если центр S удалить на бесконечно большое расстояние от p и проводить через S¥ проецирующие лучи, то они будут параллельны между собой и будут иметь общее направление s. В этом случае получаем параллельное проецирование. Аp – проекция точки A на плоскости p (рис. 2б).
Если направление при параллельном проецировании окажется перпендикулярным к плоскости проекций p, то получаемпрямоугольное, или как ещё говорят, ортогональное проецирование (рис. 2в).

| а – центральное | б – параллельное | в – ортогональное проецирование |
рис. 2. Способы проецирования
Выше было указано, что метод проекций должен устанавливать взаимно-однозначное соответствие между фигурами Ф пространства и их двумерными изображениями. Это значит, что например точке А пространства должна быть сопоставлена одна и только одна проекция Аp на плоскости p и наоборот, для проекции Аp должна быть сопоставлена единственная точка А пространства. Как видим (рис. 3) с одним аппаратом проецирования, обратное утверждение не имеет смысла, т.е. по одной проекции нельзя судить ни о положении точки в пространстве, ни о форме или размерах какого-либо объекта.
Установить указанное выше взаимно однозначное соответствие оказалось возможным при использовании двухаппаратов проецирования (рис. 4). При этом проецирование центральное либо параллельное может быть осуществлено на одну или на две плоскости проекций. В этом случае каждая точка или фигура пространства изображается в виде двух проекций (изображений), по которым можно определить положение точки или фигуры в пространстве, а значит, и форму и размеры любой фигуры, заданной определённым множеством точек. Этотметод получил название методадвух изображений.


Рис. 3 Рис. 4
Наиболее удобным в инженерной машиностроительной практике оказался так называемый метод двух ортогональных проекций. В этом методе использованы два аппарата ортогонального проецирования: первый – плоскость проекций π1 и проецирующие лучи, перпендикулярные к π1 и второй – плоскость проекций π2 и проецирующие лучи, перпендикулярные к π2. При этом плоскости π1 и π2 взаимно перпендикулярны.
Положительные качества этого метода – простота построения изображений и возможность определять размеры объекта по чертежу. Недостаток – отсутствие наглядности.
Для обеспечения хорошей наглядности и достаточной простоты построения изображений в начертательной геометрии используетсяметод аксонометрического проецирования. В этом методе осуществляется параллельное проецирование пространственных объектов вместе с системой координат, к которой они отнесены, на специально выбранную плоскость проекций p(рис 5). Так как одна параллельная проекция не определяет положения объекта в пространстве и не позволяет установить его форму, то следует строить не только аксонометрическую проекцию объекта, например А0, но и одну из ортогональных проекций объекта, например А0'.
Введём обозначения:
p – плоскость аксонометрических проекций,
s – направление проецирования;
x0, y0, z0 – аксонометрические оси, полученные в результате проецирования осей х, у и z на плоскостьp;
00 – начало аксонометрических координат.
Так как в общем случае оси х, у и z не параллельны плоскости p, то они проецируются на p с искажением (уменьшением). Поэтому при построении аксонометрических проекций необходимо учитывать коэффициенты искажения по аксонометрическим осям, т.е. kXo, kYo и kZo.
В зависимости от положения плоскости p относительно системы координат и от направления проецирования s возможны различные виды аксонометрических проекций.
Выберем плоскость аксонометрических проекций pпараллельно фронтальной плоскости x0z декартовой системы координат – рис. 5. В этом случае оси х и z проецируются на p без искажения, т.е. kXo:kZo=1:1. Если при этом направление s проецирования выберем таким, что на плоскости p угол между осями х0 и у0 станет равен 45° и коэффициент kYo искажения по оси у будет равен ½, то получим аксонометрическую проекцию под названием фронтальная диметрия.
На рис. 5 изображена графическая модель четвертей пространства, выполненная во фронтальной диметрии. По этому наглядному изображению удобно изложить суть построения ортогональных проекций точки.
Более подробное изложение материала по аксонометрическим изображениям приводится в разделе «Проекционное черчение» при изучении инженерной графике.

Произвольная аксонометрия Диметрия
Рис. 5
1.4. Инвариантные свойства проецирования
Существуют основные, т.е. неопределяемые понятия начертательной геометрии. К ним относятся точка, прямая, плоскость, множество, расстояние, принадлежность, параллельность и непрерывность.
Прежде чем переходить к изучению изображений прямой, плоскости, поверхности или их сочетаний, рационально выделить инвариантные свойства геометрических фигур, т.е. те свойства, которые сохраняются после проецировании на любую из плоскостей проекций. Этих основных свойств всего восемь, причем инварианты 1, 2, 3 и 4 характерны для любого способа проецирования, а инварианты 5, 6, 7 и 8 только для параллельного проецирования.
1-й инвариант.
Проекция точки есть точка (рис. 6), т.е. точка проецируется в точку (А→Аπ). Это инвариантное свойство вытекает из самого определения понятия проекции, как точки пересечения проецирующего луча с плоскостью проекций.
2-й инвариант.
Проекция линии (прямой) есть линия (прямая). Это инвариантное свойство вытекает из 1-го инварианта. Так как линия – это последовательность точек, то последовательность проекций этих точек даст проекцию линии. На рис. 7 приведен пример проецирования отрезка [AB] на плоскость проекций π ([AB]→[AπBπ]).
3-й инвариант.
Инвариант принадлежности. Если фигура Ф1 принадлежит фигуре Ф2, то проекция фигуры Ф1 будет принадлежать проекции фигуры Ф2. Например, если точка принадлежит прямой (рис. 8), то и проекция этой точки будет принадлежать проекции этой прямой (C [AB] Þ CπÌ[AπBπ]).


Рис. 6 Рис. 7
4-й инвариант.
Точка пересечения двух линий проецируется как точка пересечения проекций этих линий. Например (рис. 9), К = [АВ] ∩ [CD] Þ Kπ =[AπBπ] ∩ [CπDπ]. Этот инвариант является следствием инвариантов 2 и 3.


Рис. 8 Рис. 9
5-й инвариант.
Деления отрезка в заданном соотношении (теорема Фалеса). Если отрезок делится в каком-либо соотношении, то и его проекция будет делится точно в том же соотношении. Например (рис. 10), [AВ]:[CB] = [AπCπ] : [CπBπ]. Этот инвариант вытекает из того, что проецирующие лучи параллельны между собой.
6-й инвариант.
Если прямые параллельны между собой, то и их проекции тоже будут параллельны. Например (рис. 11), [AВ] ǁ [CD] Þ [AπBπ] ǁ [CπDπ]. Данный инвариант является следствием инварианта 2 и параллельности проецирующих лучей.
7-й инвариант.
Параллельность переноса объекта. Если объект перемещается параллельно самому себе, то его проекция не меняет своей формы и размеров, а меняет только свое местоположение на картине. Например (рис. 12), ∆АВС ǁ ∆А1В1С1^ ∆АВС = ∆А1В1С1 ⇒ ∆АπВπСπ = ∆А  В
В  С
С  . Данный инвариант является следствием инварианта 2 и параллельности проецирующих лучей.
. Данный инвариант является следствием инварианта 2 и параллельности проецирующих лучей.


Рис. 10 Рис. 11


Рис. 12 Рис. 13
8-й инвариант.
Если плоская фигура параллельна картинной плоскости, то ее проекция является натуральной величиной этой фигуры. Например (рис. 13), ∆АВС ‖ π⇒ ∆АπВπСπ = ∆АВС. Данный инвариант является следствием инварианта 2 и параллельности проецирующих лучей.
Эпюр точки
Чтобы получить чертёж точки А (рис. 15), в аппарате проецирования (рис. 14) плоскость π1 с полученной проекцией точки А1 вращают по часовой стрелке вокруг оси 0Х, до совмещения её с плоскостью π2. Затем плоскость π3 с проекцией точки А3, вращают против часовой стрелки вокруг оси 0Z, до совмещения её с плоскостью π2. Направление поворотов плоскостей π2 и π3 показано на рис. 13 стрелками. Полученный таким образом чертёж называется эпюром. При этом прямые А1Ах и А2Ах станут располагаться на общем к оси 0Х перпендикуляре А1А2, а прямые А2Ах и А3Ах станут располагаться на общем к оси 0Z перпендикуляре А2А3. Эти прямые в дальнейшем будем называть соответственно вертикальной и горизонтальной линиями связей.
Следует отметить, что при переходе от аппарата проецирования к эпюру проектируемый объект исчезает, но вся информация о его форме, геометрических размерах и месте его положения в пространстве сохраняются.
На практике построение эпюра точки А(xA, yA, zA) осуществляется по численным значениям ее координат xA, yA и zA в следующей последовательности (рис. 15). Эта последовательность называется методикой построения эпюра точки.
1. Ортогонально вычерчиваются оси OX, OY и OZ.
2. На оси OX откладывается численное значение координаты xA точки А и получают положение точки Ах.
3. Через точку Ах перпендикулярно оси OX проводится вертикальная линия связи.
4. На вертикальной линии связи от точки Ах по направлению оси OY откладывается численное значение координаты yA точки А и определяется положение горизонтальной проекции точки А1 на эпюре.
5. На вертикальной линии связи от точки Ах по направлению оси OZ откладывается численное значение координаты zA точки А и определяется положение фронтальной проекции точки А2 на эпюре.

Рис. 15
6. Через точку А2 параллельно оси OX проводится горизонтальная линия связи. Пересечение этой линии и оси OZ даст положение точки Аz.
7. На горизонтальной линии связи от точки Аz по направлению оси OY откладывается численное значение координаты yA точки А и определяется положение профильной проекции точки А3 на эпюре.
Характеристика точек
Все точки пространства подразделяются на точки частного и общего положений.
Точки частного положения. Точки, принадлежащие аппарату проецирования, называются точками частного положения. К ним относятся точки, принадлежащие плоскостям проекций, осям, началу координат и центрам проецирования. Характерные признаки точек частного положения приведены в табл. 1 и на рис. 16–19.
Таблица 1
Математические признаки точек частного положения
| Точка принадлежит | Численные значения координат точки | ||
| x | y | z | |
| плоскости π1 | ≠0 | ≠0 | =0 |
| плоскости π2 | ≠0 | =0 | ≠0 |
| плоскости π3 | =0 | ≠0 | ≠0 |
| оси 0X | ≠0 | =0 | =0 |
| оси 0Y | =0 | ≠0 | =0 |
| оси 0Z | =0 | =0 | ≠0 |
| точки 0 | =0 | =0 | =0 |
| центру S1 | ≠0 | ≠0 | ∞ |
| центру S2 | ≠0 | ∞ | ≠0 |
| центру S3 | ∞ | ≠0 | ≠0 |
На рис. 16 приведены характерные признаки принадлежности точек плоскостям проекций на эпюре Монжа: точка А Ì π1 (рис 16а); точка В Ì π2(рис 16б); точка С Ìπ3 (рис 16в). Такими признаками являются принадлежность двух проекций точки осям.

Рис. 16
На рис. 17 приведены характерные признаки принадлежности точек осям на эпюре Монжа: точка А Ì0X (рис 17а); точка В Ì 0Y (рис 17б); точка С Ì0Z (рис 17в). Такими признаками являются принадлежность двух тождественно совпадающих проекций точки осям эпюра.
На рис 18 на эпюре Монжа показан характерный признак точки А принадлежащей началу координат, т.е. все три проекции точки тождественно совпадают и принадлежат началу координат.
На рис. 19 приведены характерные признаки принадлежности точек центрам проецирования на эпюре Монжа: точка А Ì S1 (рис 19а); точка В Ì S2(рис 19б); точка С Ì S3 (рис 19в). Такими признаками являются принадлежность двух проекций точки проекциям центров проецирования.

Рис. 17

Рис. 18

Рис. 19
Точки общего положения. К точкам общего положения относятся точки, не принадлежащие аппарату проецирования. Например, точка на рис. 13.
В общем случае численные значения координат точки характеризует ее удаление от плоскости проекций: координата х от плоскостиπ3; координата y от плоскости π2; координата z от плоскости π1. Следует отметить, что знаки при численных значениях указывают на направление удаления точки от плоскостей проекций. В зависимости от сочетания знаков при численных значениях координат точки зависит в каком из октанов она находится (табл. 2).
Расположение проекций точки, относительно осей, на эпюре зависит от того в каком октане она находится (рис. 20).

Рис. 20
Таблица 2
Определение номера октана от знаков координат
| Номер октана | Знак при координате | ||
| x | y | z | |
| I | + | + | + |
| II | + | - | + |
| III | + | - | - |
| IV | + | + | - |
| V | - | + | + |
| VI | - | - | + |
| VII | - | - | - |
| VIII | - | + | - |
На рис. 20 показано расположение проекций относительно осей для точки: А находящейся в I октане; В находящейся во II октане; C находящейся в III октане; D находящейся в IV октане; E находящейся в V октане; G находящейся в VI октане; K находящейся в VII октане; L находящейся в VIII октане.
Метод двух изображений
Аппарат проецирования для метода двух изображений. На практике, кроме метода полного проецирования используют метод двух изображений. Он отличается тем, что в этом методе исключается третья проекция объекта. Для получения аппарата проецирования метода двух изображений из аппарата полного проецирования исключается профильная плоскость проекций с ее центром проецирования (рис. 20). Кроме того, на оси 0Х назначается начало отсчета (точка 0) и из него перпендикулярно оси 0Х в плоскостях проекций π1иπ2 проводят оси 0Y и 0Z соответственно.

Рис. 20
В этом аппарате все пространство делится на четыре квадранта. На рис. 20 они обозначены римскими цыфрами.
Плоскости проекций считаются непрозрачными, а зритель всегда находится в I квадранте.
Рассмотрим работу аппарата на примере проецирования точки А.
Из центров проецирования S1 и S2 выходят проецирующие лучи l1 и l2. Эти лучи проходят через точку А и пересекаясь с плоскостями проекций образуют ее проекции:
– А1 – горизонтальная проекция точки А;
– А2 – фронтальная проекция точки А.
Эпюр точки методом двух изображений. Чтобы получить эпюр точки А (рис. 21), в аппарате проецирования (рис. 20) плоскость π1 с полученной проекцией точки А1 вращают по часовой стрелке вокруг оси 0Х, до совмещения её с плоскостью π2. Направление поворота плоскости π1 показана на рис. 20 стрелками. При этом на эпюре точки полученной методом двух изображений остается только одна вертикальная линия связи А1А2.

Рис. 21
На практике построение эпюра точки А(xA, yA, zA) осуществляется по численным значениям ее координат xA, yA и zA в следующей последовательности (рис. 21).
1. Вычерчивается ось OX и назначается начало отсчета (точка 0).
2. На оси OX откладывается численное значение координаты xA точки А и получают положение точки Ах.
3. Через точку Ах перпендикулярно оси OX проводится вертикальная линия связи.
4. На вертикальной линии связи от точки Ах по направлению оси OY откладывается численное значение координаты yA точки А и определяется положение горизонтальной проекции точки А1 на эпюре. Следует отметить, что на эпюре ось OY не вычерчивается, а предполагается, что ее положительные значения располагаются ниже оси OX, а отрицательные выше.
5. На вертикальной линии связи от точки Ах по направлению оси OZ откладывается численное значение координаты zA точки А и определяется положение фронтальной проекции точки А2 на эпюре. Следует отметить, что на эпюре ось OZ не вычерчивается, а предполагается, что ее положительные значения располагаются выше оси OX, а отрицательные ниже.
Характеристика точек в методе двух изображений. Характерные признаки точек частного положения на эпюре Монжа (рис. 22):


Рис. 22 Рис. 23
– точки, принадлежащие плоскостям проекций – одна из проекций точки принадлежит оси 0Х (А Ì π1, В Ì π2);
– точки, принадлежащие оси 0Х – оби проекции точки тождественно совпадают и принадлежат ось (С Ì0Х);
– точки, принадлежащие центрам проецирования – одна из проекций точки располагается в бесконечности от оси 0Х (D Ì S1, E Ì S2).
Расположение проекций точек общего положения на эпюре Монжа в зависимости от квадранта в котором они находятся приведены на рис. 23: точка А находящейся в I квадранте; В находящейся во II квадранте; C находящейся в III квадранте; D находящейся в IV квадранте.
Конкурирующие точки
Точки на одном проецирующем луче называются конкурирующими. Они в направлении проецирующего луча имеют общую для них проекцию, т.е. их проекции тождественно совпадают. Характерным признаком конкурирующих точек на эпюре является совпадение их одноименных проекций. Конкуренция заключается в видимости их проекций относительно наблюдателя. Говоря другими словами, в пространстве для наблюдателя одна из точек видима, другая – нет. И, соответственно, на чертеже: одна из проекций конкурирующих точек видима, а проекция другой точки – невидима.
На пространственной модели проецирования (рис. 24) из двух конкурирующих точек А и В видима точка А по двум взаимно дополняющим признакам. Судя по цепочке S1→А→В точка А ближе к наблюдателю, чем точка В. И, соответственно, – дальше от плоскости проекций π1 (т.е. zA > zA).

Рис. 24 Рис.25
Если видима сама точка A, то видима и её проекция A1. По отношению к совпадающей с ней проекцией B1. Для наглядности и при необходимости на эпюре невидимые проекции точек принято заключать в скобки.
Уберем на модели точки А и В. Останутся их совпадающие проекции на плоскости π1 и раздельные проекции – на π2. Условно оставим и фронтальную проекцию наблюдателя (⇩), находящегося в центре проецирования S1. Тогда по цепочке изображений ⇩ → A2 → B2 можно будет судить о том, что zA > zB и что видима и сама точка А и её проекция А1.
Аналогично рассмотрим конкурирующие точки С и D по видимости относительно плоскости π2. Поскольку общий проецирующий луч этих точек l2параллелен оси 0Y, то признак видимости конкурирующих точек С и D определяется неравенством yC > yD. Следовательно, что точка D закрыта точкой С и соответственно проекция точки D2 будет закрыта проекцией точки С2 на плоскости π2.
Рассмотрим, как определяется видимость конкурирующих точек на комплексном чертеже (рис. 25).
Судя по совпадающим проекциям А1≡В1 сами точки А и В находятся на одном проецирующем луче, параллельном оси 0Z. Значит сравнению подлежат координаты zA и zB этих точек. Для этого используем фронтальную плоскость проекций с раздельными изображениями точек. В данном случае zA > zB. Из этого следует, что видима проекция А1.
Точки C и D на рассматриваемом комплексном чертеже (рис. 25) так же находятся на одном проецирующем луче, но только параллельном оси 0Y. Поэтому из сравнения yC > yD делаем вывод, что видима проекция С2.
Общее правило. Видимость для совпадающих проекций конкурирующих точек определяется сравнением координат этих точек в направлении общего проецирующего луча. Видима та проекция точки, у которой эта координата больше. При этом сравнение координат ведется на плоскости проекций с раздельными изображениями точек.
Задача определения видимости конкурирующих точек имеет большое практическое значение. Поскольку окончательная обводка чертежа геометрической фигуры производится с учетом видимости её элементов.
1.10. Контрольные вопросы
1. Что изучает начертательная геометрия?
2. Какие задачи решает начертательная геометрия?
3. Что называется чертежом?
4. Какие специальные символы существуют для обозначения параллельности, перпендикулярности, пересечения, скрещивания? Какие обозначения вы знаете, кроме этих?
5. Основные элементы аппарата проецирования.
6. Виды проецирования.
7. В чем сущность центрального проецирования?
8. В чем сущность параллельного проецирования?
9. Чем отличается ортогональное проецирование от косоугольного?
10. Как проецируются точка и линия?
11. В чем заключается сущность инвариантов «Точка пересечения двух линий», «Принадлежность» и «Параллельность переноса объекта»?
12. Как называются плоскости проекций π1,π2и π3?
13. Как образуются оси 0Х, 0Y и 0Z?
14. Как получается проекции точи в аппарате проецирования?
15. Зачем нужны центры проецирования S1, S2 и S3?
16. Как осуществляется переход от аппарата проецирования к плоскому чертежу?
17. Чем отличается эпюр от аппарата проецирования?
18. Алгоритм построения точки на эпюре Монжа.
19. Какие точки относятся к точкам общего положения?
20. Какие точки относятся к точкам частного положения?
21. Характерные признаки точек частного положения на эпюре Монжа.
22. Что характеризуют численные значения координат х, y и z точки?
23. В чем заключается сущность метода двух изображений и чем он отличается от метода трех изображений?
24. Характерные признаки точек общего и частного положений на эпюре при использовании метода двух изображений?
25. Какие точки называются конкурирующими и в чем заключается их конкуренция?
26. Характерный признак конкурирующих точек на эпюре и порядок определения видимости их проекций.
Задание прямой на эпюре
Чтобы построить прямую на эпюре необходимо на прямой взять две точки и спроецировать их на плоскости проекций (рис. 26). Затем проведя прямые через одноименные проекции точек получим проекции прямой.
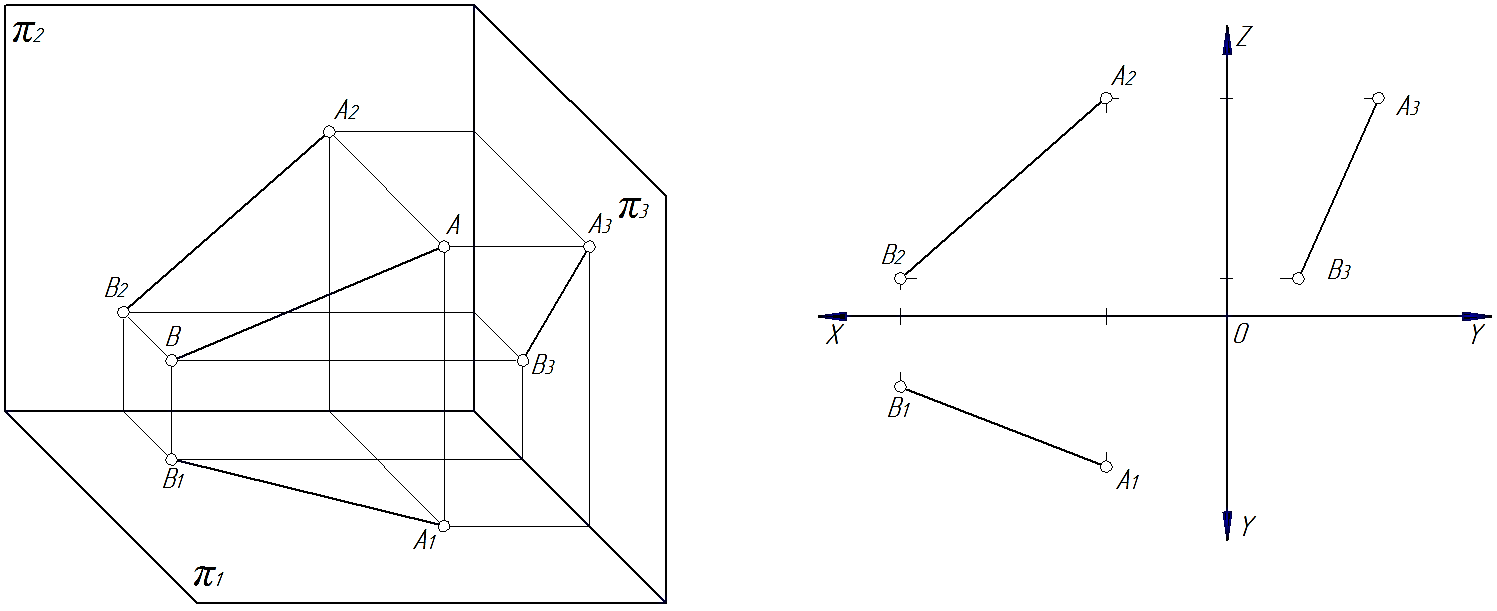
Рис. 26
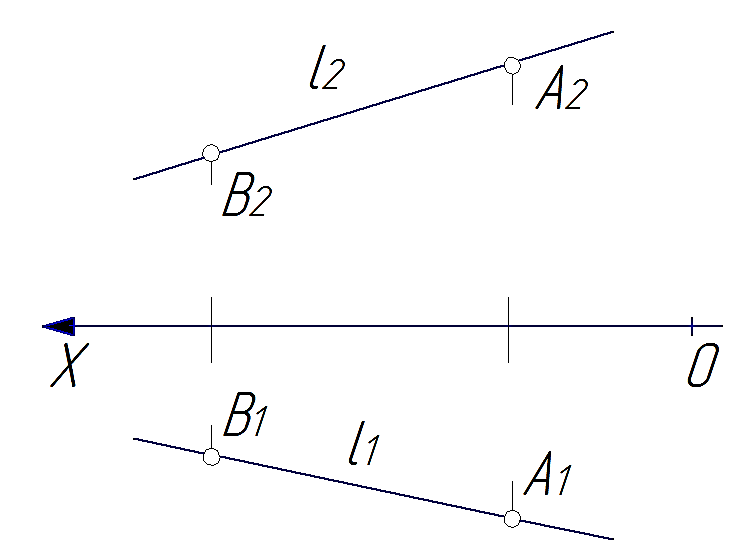 Рис. 27 Рис. 27 |
В общем случае прямые в пространстве могут задаваться (рис. 27) двумя точками (точки А и В), отрезком ([АВ]) или точкой и направлением прямой (например, точкой А и условиями, характеризующими направление прямой).
Примечание. В последующем все эпюры будут выполнятся методом двух изображений и только при необходимости будет использоваться полное проецирование (метод трех изображений).
Характеристика прямых
Все прямые пространства подразделяются на прямые общего и частного положений.
Прямая общего положения. Прямая общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций.
Примеры таких прямых показаны на рис. 26 и 27.
Особенностью изображения этих прямых является то, что на эпюре проекции прямой составляют с осями проекций произвольные углы и поэтому величина каждой проекции меньше истинной величины самой прямой (рис. 26).
Прямая частного положения. Прямые, параллельные или перпендикулярные плоскостям проекций называют прямыми частного положения.
Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня.
1. Прямые, параллельные горизонтальной плоскости проекций; называют горизонтальными или горизонталями h (рис. 28).
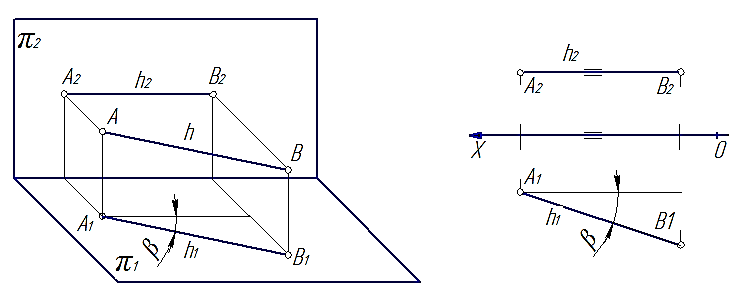
Рис. 28
Характерным признаком таких прямых на эпюре является то, что их фронтальные проекции параллельны оси 0Х.
2. Прямые, параллельные фронтальной плоскости проекций; называют фронтальными или фронталями f (рис. 29).
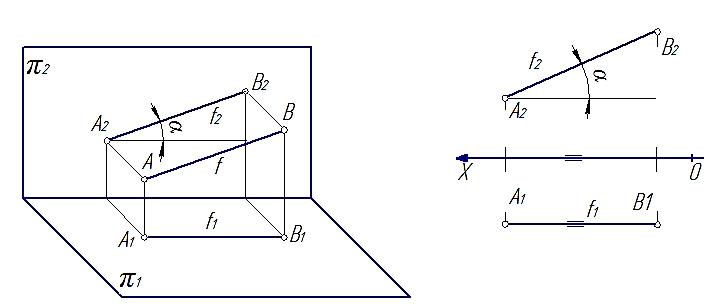
Рис. 29
Характерным признаком таких прямых на эпюре является то, что их горизонтальные проекции параллельны оси 0Х.
3. Прямую, параллельную профильной плоскости проекций, называют профильной р (рис. 30).
Характерным признаком таких прямых на эпюре является то, что их горизонтальные и фронтальные проекции перпендикулярны оси 0Х.
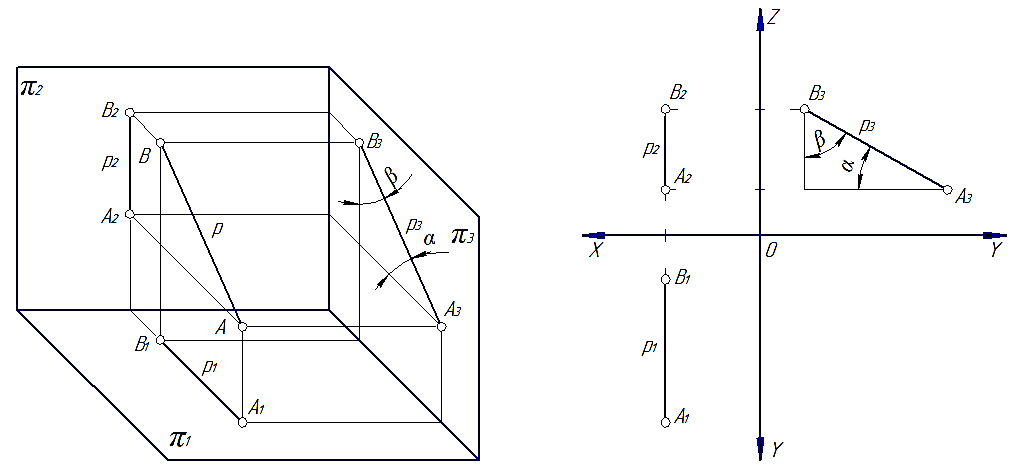
Рис. 30
Следует отметить, что каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона a и b, которые эта прямая образует с двумя другими плоскостями проекций, так же будут проецироваться на эту плоскость без искажения.
Так на рис. 28 проекция [A1B1]=[AB], а угол b – угол наклона отрезка [AB] к плоскости π2. На рис. 29 проекция [A2B2]=[AB], а угол a – угол наклона отрезка [AB] к плоскости π1. На рис. 30 видно, что все проекция [A2B2]=[AB], а углы a и b – углы наклона отрезка [AB] к плоскостям π1 и π1 соответственно.
Прямые уровня могут принадлежать плоскостям проекций. Та
