Пересечение прямой с плоскостью

Определение точки встречи прямой общего положения с плоскостью общего положения.

Рассмотрим пример решения задачи на комплексном чертеже (рис. 23).

Задана плоскость α(∆АВС) и прямая l. Определить точку встречи прямой с плоскостью и ее видимость относительно плоскости ограниченной треугольником ∆АВС: К=l∩α(∆АВС). Варианты заданий приведены в табл. 7.

Решение. Заключаем прямую n во вспомогательную горизонтально проецирующую плоскость β, которую зададим горизонтальным следом β₁ (горизонтальная проекция плоскости). Причем след β₁ должен совпадать с горизонтальной проекцией прямой n₁. Далее находим прямую l пересечения вспомогательной плоскости β с заданной плоскостью α. Сторона АВ пересекается с плоскостью β в точке 1, а сторона АС – в точке 2. Сначала отмечаем горизонтальные проекции точек 1₁ и 2₁, а затем с помощью вертикальных линий связи находим фронтальные проекции точек 1₂ и 2₂ соответственно на фронтальных проекциях сторон треугольника А₂В₂ и А₂С₂. Таким образом, плоскости пересекаются по прямой l(1 2). Теперь можно определить фронтальную проекцию К₂ искомой точки. Она будет являться точкой пересечения фронтальных проекций построенной прямой l(1₂2₂) и заданной прямой n₂. Горизонтальная проекция К₁ определяется с помощью вертикальной линии связи на горизонтальной проекции прямой n₁.

Рис. 23

Затем нужно определить видимость прямой n относительно плоскости α. Для определения видимости на необходимо воспользоваться горизонтально конкурирующими точками 2 и 3 (точка 2 лежит на стороне АС треугольника, а точка 3 – на прямой n). Видимость прямой на π₂ определяем с помощью фронтально конкурирующих точек 4 и 5 (точка 5 лежит на стороне ВС, а точка 4 – на прямой n). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символами «↑» и «↓».

Определение точки встречи прямой общего положения с проецирующей плоскостью.

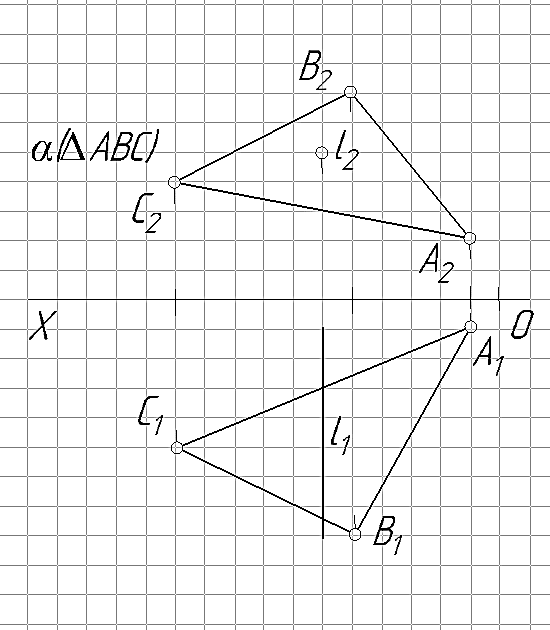
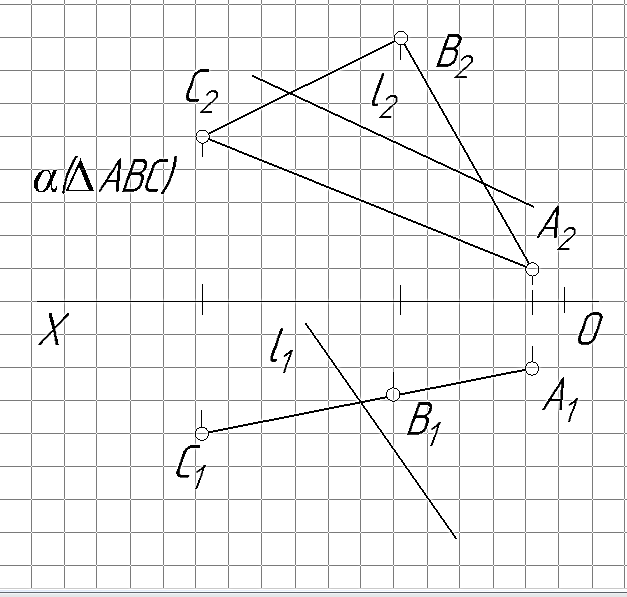
Постановка задачи. Пусть задана горизонтально-проецирующая плоскость α треугольником ∆АВС и прямая l общего положения (рис. 24). Необходимо определить точку встречи К прямой l с плоскость α: К =l∩α. Варианты заданий приведены в табл. 8.

Решение. Проекция точки встречи К₁ прямой l с плоскостью α однозначно определяется как точка пересечения вырожденной в прямую горизонтальной проекции плоскости с одноименной проекцией прямой: К₁=l₁∩α₁(∆A₁B₁C₁).

Недостающая фронтальная проекция точки встречи К₂ находится по принадлежности точка К прямой l: КÌl => К₁Ìl₁.

Видимость прямой l относительно плоскости α определяется только для фронтальной плоскости проекций, т.к. на π₁ обе проекции видны. Видимость определяется с помощью фронтально конкурирующих точек 1 и 2 (точка 2 лежит на стороне ВС треугольника, а точка 1 – на прямой l). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символом «↑».В задачах, где используется фронтально-проецирующая плоскость, при определении точки встречи последовательность решения аналогична выше указанному, только в них известной является фронтальная проекция искомой точки.

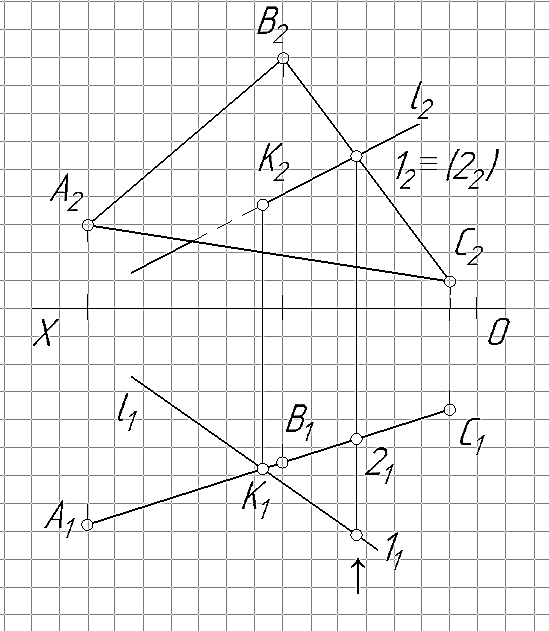
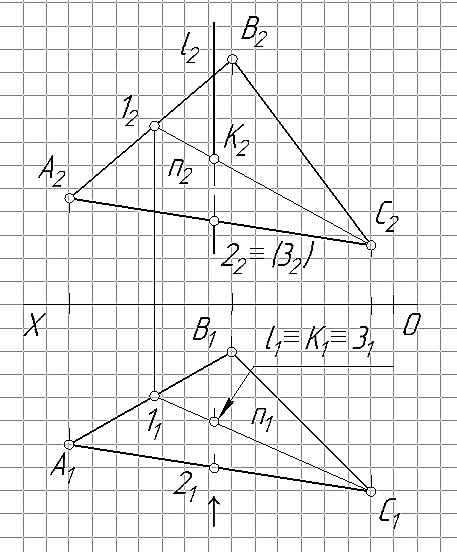
Рис. 24 Рис. 25

Определение точки встречи проецирующей прямой с плоскостью общего положения.

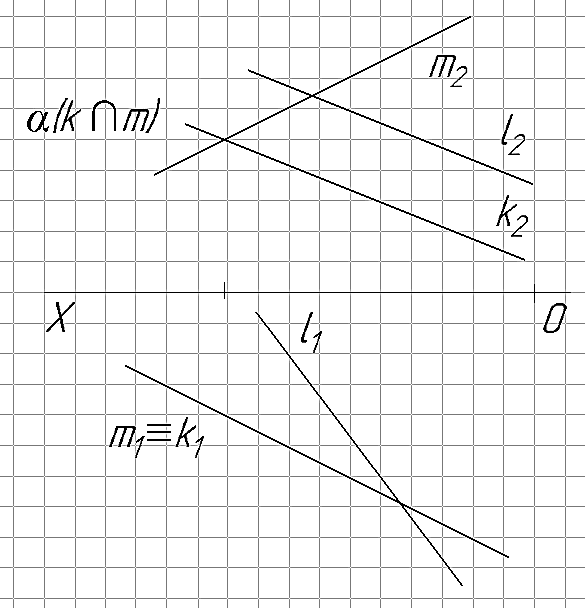
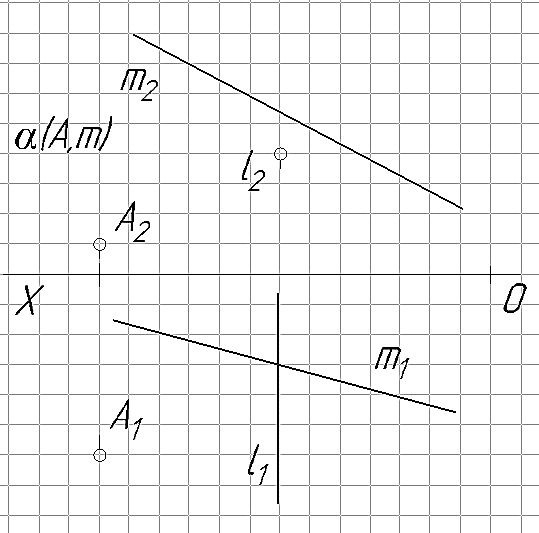
Постановка задачи. Пусть задана горизонтально-проецирующая прямая l (рис. 31) и плоскость общего положения α(∆АВС). Необходимо определить точку встречи К прямой l с плоскость α: К =n∩α. Варианты заданий приведены в табл. 8.

Решение. Очевидно проекция точки встречи К₁ прямой с плоскостью α совпадает с вырожденной проекцией прямой l₁: К₁ ≡l₁: Учитывая то, что точка К принадлежит плоскости α, то задача сводится к определению недостающей проекции точки принадлежащей плоскости. Для этого, вначале, через вырожденную проекцию l₁ проводится проекция вспомогательной прямой n₁ в предположении, что эта прямая n принадлежит плоскости α: nÌα => n₁Ìα₁. Затем, достраивается недостающая фронтальная проекция этой прямой n₂. Точка пересечения фронтальных проекций заданной l₂ и вспомогательной n₂ прямых является искомой проекцией точки встречи К₂.

Видимость прямой l относительно плоскости α определяется только для фронтальной плоскости проекций, т.к. на π₁ обе проекции видны. Видимость определяется с помощью фронтально конкурирующих точек 2 и 3 (точка 2 лежит на стороне АС треугольника, а точка 3 – на прямой l). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символом «↑».

В задачах, где используется фронтально-проецирующая прямые, при определении точки встречи последовательность решения аналогична выше указанному, только в них известной является фронтальная проекция искомой точки.

Таблица 7

Исходные данные по темам «Пересечение прямой общего положения с плоскостью общего положения»

Продолжение табл. 7

Продолжение табл. 7

Окончание табл. 7

Таблица 8

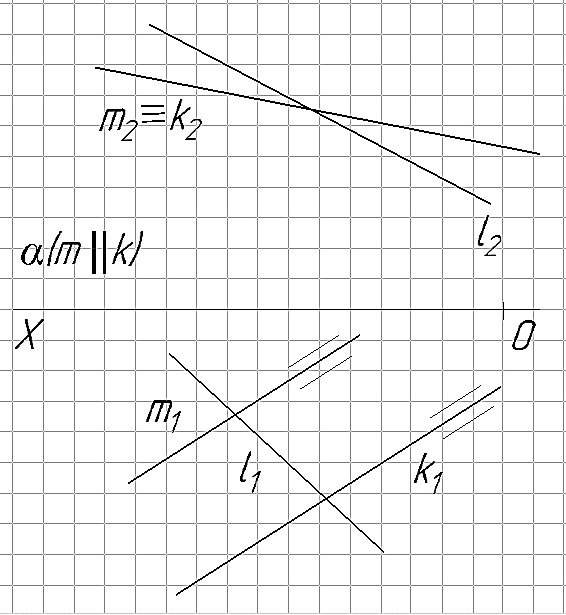
Исходные данные по темам: «Пересечение прямой с плоскостью – частные случаи»

Продолжение табл. 8

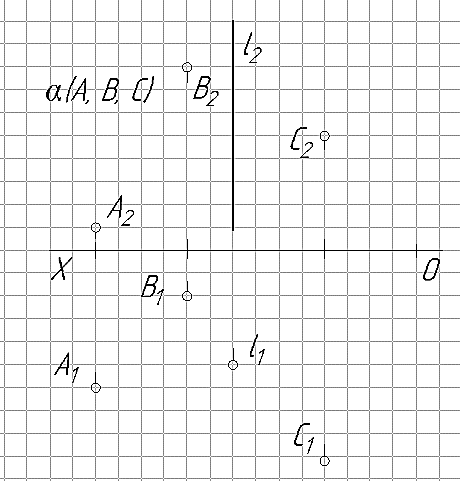Продолжение табл. 8

Окончание табл. 8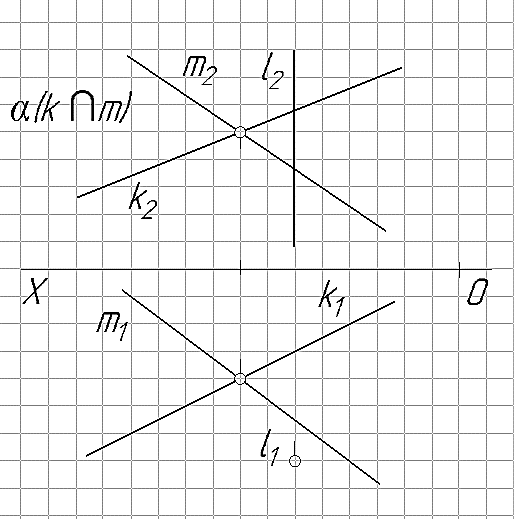