Алгоритм Мичнера для построения окружности
В данном алгоритме окружность строится во втором октанте из начальной точки (0, R) по часовой стрелке. Остальные части окружности достраиваются по алгоритму, описанному выше. Так как построение ведется во втором октанте, то имеется только две приоритетные точки, по которым можно продолжать построение: (xi + 1, yi) и (xi + 1, yi – 1). В данном алгоритме рассматриваются две погрешности и их сумма:
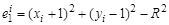 ;
;
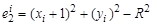 ;
;
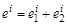 .
.
Если ei > 0, то выбираем точку (xi + 1, yi – 1), иначе – точку
(xi + 1, yi).
Для итеративной организации алгоритма необходимо определить выражение для ei+1, оно зависит от выбора следующей точки:
– для точки (xi + 1, yi) – ei+1 = ei + 4*xi + 6;
– для точки (xi + 1, yi – 1) – ei+1 = ei + 4*(xi – yi) + 10;
– для начальной точки (R, 0) e1 = 3 – 2*R.

Задание на лабораторную работу № 3
"Алгоритмы генерации окружности"
1. Центр окружности находится в середине экрана (как вариант, координаты центра окружности вводятся вручную).
2. На экране изображается сетка псевдопикселов.
3. Постройте окружность с заданным радиусом по целочисленному алгоритму Брезенхема, используя псевдопикселы.
4. Постройте другим цветом "настоящую" окружность.
5. Сравните полученные результаты. Сделайте выводы.
6. Вариант работы: использование алгоритма Мичнера или любого другого алгоритма построения окружности.
7. Назовите критерий выбора следующей точки в алгоритме Брезенхема.
8. Сравните два алгоритма.
 4. Алгоритмы построчного заполнения
4. Алгоритмы построчного заполнения
многоугольников
ъ Цель: Изучить алгоритмы построчного заполнения
многоугольников
Простейший метод заполнения многоугольника – проверка на принадлежность к многоугольнику каждого элемента растра, но этот метод слишком неэффективен.
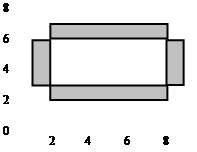
Следующий шаг – прямоугольная оболочка – наименьший прямоугольник, содержащий данную фигуру (рис. 4.1,а). Но в случае, изображенном на рис. 4.1,б, эффективность алгоритма тоже оставляет желать лучшего.
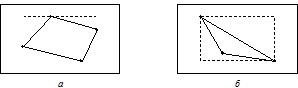
Рис. 4.1. Прямоугольная оболочка
Более эффективный метод заполнения состоит в следующем.
Для растровых устройств соседние пикселы в сканирующей строке, вероятно, имеют одинаковые характеристики. Они меняются только там, где ребро многоугольника пересекает сканирующую строку. Эти пересечения делят строку на области (рис. 4.2).
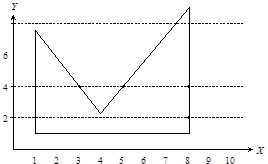
Рис. 4.2. Простейший метод заполнения многоугольника
Для строки Y = 2:
X < 1 – цвет закраски – фон;
1 ≤ X ≤ 8 – цвет закраски – цвет многоугольника;
X > 8 – цвет закраски – фон.
Для строки Y = 4:
X < 1 – цвет закраски – фон;
1 ≤ X ≤ 3 – цвет закраски – цвет многоугольника;
3 < X < 5 – цвет закраски – фон;
5 ≤ X ≤ 8 – цвет закраски – цвет многоугольника;
X > 8 – цвет закраски – фон.
Для определения интенсивности и цвета пикселов рассматриваются пары отсортированных точек пересечения по возрастанию X.
Для строки Y = 2: 1, 8.
Для строки 4: 1, 3, 5, 8 и закрашивается область между парами, остальное – фон.
Трудности возникают при пересечении вершин (рис. 4.3).
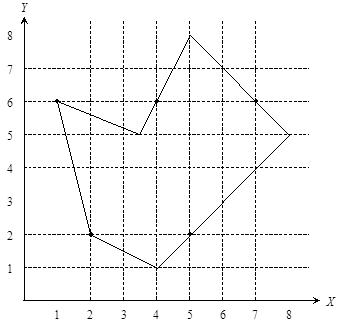
Рис. 4.3. Пересечение вершин сканирующими строками
Для строки Y = 2 точки пересечения: 2, 2, 5, т.е. нечетное количество пересечений и, следовательно, необходимо учитывать только одну точку пересечения с ребрами (а именно, 2, 5).
Однако при использовании этого критерия, для строки Y = 6 получаем точки пересечения: 1, 4, 7, т.е. опять нечетное количество пересечений и, в данном случае, необходимо учитывать точку (1, 6) дважды – (1, 1, 4, 7).
Вывод: если точка пересечения является локальным максимумом или минимумом, то учитываются две точки пересечения, иначе – одна. Для определения локальных максимумов и минимумов применяется следующий алгоритм: если координаты Y концов отрезков больше (меньше), чем у точки пересечения, то это локальный минимум (максимум) и учитывается две точки, иначе – одна.
Другой простой метод заполнения многоугольников – алгоритм заполнения по ребрам: для каждой сканирующей строки, пересекающей ребро многоугольника, инвертировать все пикселы, которые лежат справа от точки пересечения. Повторить для каждого ребра, кроме ребер, параллельных оси абсцисс (рис. 4.4). Инверсия означает изменение цвета многоугольника на цвет фона и наоборот.
Исходный многоугольник изображен на рис. 4.4,а). Ребро P1 – P2 параллельно оси абсцисс и, следовательно, его не учитываем. Обработке ребра P2 – P3 соответствует рис. 4.4,б), ребра P3 – P4 – рис. 4.4,в), ребра P4 – P5 – рис. 4.4,г) и, наконец, ребра P5 – P1 – рис 4.4,д). Причем ребра многоугольника можно обрабатывать
в произвольном порядке. Недостатком этого метода является многократная обработка "правых" пикселов.

Задание на лабораторную работу № 4
"Алгоритмы построчного заполнения
многоугольников"
1. Построить многоугольник (при этом должны быть использованы локальные максимумы или минимумы координат вершин).
2. Используя один из алгоритмов, закрасить многоугольник.
3. При этом при построчном заполнении – ввести програм-мную задержку после прохождения очередной сканирующей строки, а при заполнении по ребрам ввести задержку после обработки каждого ребра.
4. Сравните алгоритмы.
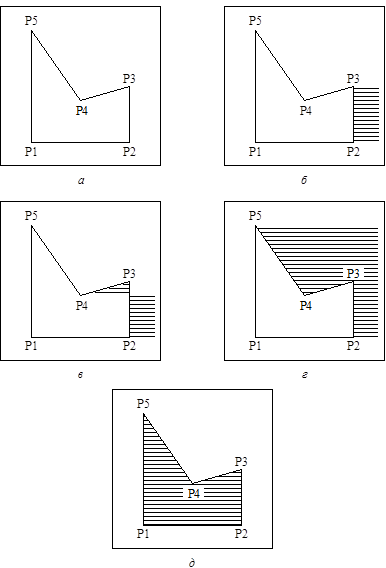
Рис. 4.4. Пример алгоритма заполнения по ребрам
Заливка области с затравкой

Цель: Изучить алгоритмы заливки области с затравкой.
Понять, в чем основное отличие
заливки области от заполнения многоугольника
Заливка области с затравкой
По способу задания области делятся на два типа (рис. 5.1):
· гранично-определенные, задаваемые своей (замкнутой) границей такой, что коды пикселов, границы которых отличны от кодов внутренней, перекрашиваемой части области. На коды пикселов внутренней части области налагаются два условия – они должны быть отличны от кода пикселов границы и кода пиксела перекраски. Если внутри гранично-определенной области имеется еще одна граница, нарисованная пикселами с тем же кодом, что и внешняя граница, то соответствующая часть области не должна перекрашиваться;
· внутренне-определенные, нарисованные одним определенным кодом пиксела. При заливке этот код заменяется на новый код закраски.
Основное отличие заливки области с затравкой от заполнения многоугольника: в последнем случае мы сразу имеем всю информацию о предельных размерах части экрана, занятой многоугольником. Поэтому определение принадлежности пиксела многоугольнику базируется на быстро работающих алгоритмах, использующих когерентность строк и ребер (см. предыдущий раздел). В алгоритмах же заливки области с затравкой нам вначале надо прочитать пиксел, затем определить, принадлежит ли он области и, если принадлежит, то перекрасить.
Заливаемая область или ее граница – некоторое связное множество пикселов. По способам доступа к соседним пикселам области делятся на 4- и 8-связные. В 4-связных областях доступ к соседним пикселам осуществляется по четырем направлениям – горизонтально влево и вправо и вертикально – вверх и вниз.
В 8-связных областях к этим направлениям добавляются еще
4 диагональных. Используя связность, мы можем, двигаясь от точки затравки, достичь и закрасить все пикселы области.
 | |||||||||
а
 |
 | |||||||||
б
Рис. 5.1. Деление области по способу задания:
а – внутренне-определенная область;
б – гранично-определенная область
Важно отметить, что для 4-связной прямоугольной области граница 8-связна (рис. 5.2,а) и, наоборот, у 8-связной области граница 4-связна (рис. 5.2,б). Поэтому заполнение 4-связной области 8-связным алгоритмом может привести к "просачиванию" через границу и заливке пикселов в примыкающей области.

а б
Рис. 5.2. Связанность областей:
а – 4-связные; б – 8-связные, внутренне-определенные области

 – пикселы области; – пикселы границы
– пикселы области; – пикселы границы
В общем, 4-связную область мы можем заполнить как 4-, так и 8-связным алгоритмом. Обратное же неверно.
С использованием связности областей и стека можно построить простые алгоритмы закраски как внутренне, так и гранично-определенной области.
Простой алгоритм заливки
Рассмотрим простой алгоритм заливки гранично-определенной 4-связной области. Заливка выполняется следующим образом:
· определяется, является ли пиксел граничным или уже закрашенным;
· если нет, то пиксел перекрашивается, затем проверяются и, если надо, перекрашиваются 4 соседних пиксела.
Ниже приведен итеративный алгоритм закраски 4-связной гранично-определенной области. Логика работы алгоритма следующая:
· поместить координаты затравки в стек;
· пока стек не пуст;
· извлечь координаты пиксела из стека;
· перекрасить пиксел;
· для всех четырех соседних пикселов проверить, является ли он граничным или уже перекрашен.
· если нет, то занести его координаты в стек.
На рис. 5.3,а а показан выбранный порядок перебора соседних пикселов, а на рис. 5.3,б – соответствующий ему порядок закраски простой гранично-определенной области.
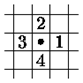 а а | 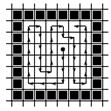 б б |
Рис. 5.3. Заливка 4-связной области итеративным алгоритмом:
a – порядок перебора соседних пикселов;
б – порядок заливки области
Рассмотренный алгоритм легко модифицировать для работы с 8-связными гранично-определенными областями или же для работы с внутренне-определенными.
Как уже отмечалось, очевидный недостаток алгоритмов, непосредственно использующих связность закрашиваемой облас-ти, – большие затраты памяти на стек, так как на каждый закрашенный пиксел в стеке по максимуму будет занесена информация о еще трех соседних. Кроме того, информация о некоторых пикселах может записываться в стек многократно. Это приведет не только к перерасходу памяти, но и к потере быстродействия за счет многократной раскраски одного и того же пиксела.
