Построение гипоциклоиды аналогично описанному для эпициклоиды.

НАНЕСЕНИЕ РАЗМЕРОВ

ГОСТ 2.307–68 (в ред. 2004 г.) устанавливает правила нанесения размеров и предельных отклонений на чертежах и других технических документах на изделия всех отраслей промышленности и строительства.

ПРАВИЛА И РЕКОМЕНДАЦИИ ПРИ ПРОСТАНОВКЕ РАЗМЕРОВ

Величину изображенного изделия и его элементов задают размерами, указываемыми на чертеже размерными числами и размерными линиями, используют при необходимости выносные линии (рисунок 80).

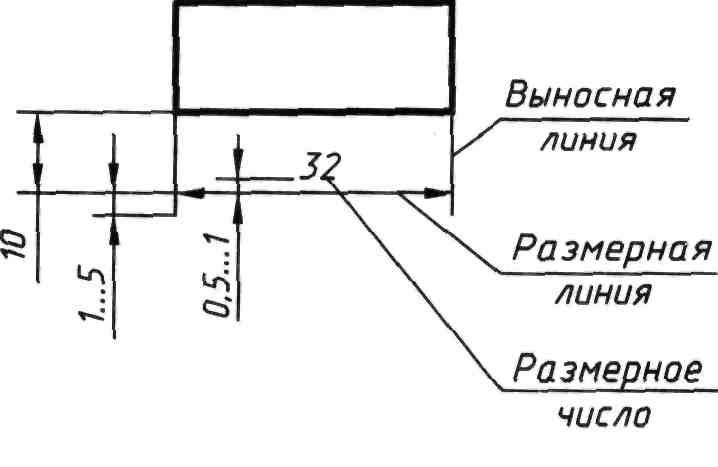
Рисунок 80

Общее количество размеров на чертеже должно полностью и однозначно определять размеры формы объекта. Размеры, проставляемые на чертеже, должны соответствовать действительной величине объекта и не зависеть от масштаба его изображения.

Каждый размер наносят на чертеже один раз. Расположение размеров должно обеспечивать удобство их прочтения.

Объекты имеют размеры трех основных типов: размеры формы (линейные и угловые), размеры положения (линейные) и размеры ориентации (угловые).

Единичный объект, тем более объект простой формы, располагают на чертеже в системе плоскостей проекций V, Н, W так, чтобы его ориентация была задана наиболее лаконично.

Многогранник располагают так, чтобы наибольшее количество его граней, т.е. отсеков его оболочки, было параллельно или перпендикулярно основным плоскостям проекций.

Тела вращения располагают так, чтобы их оси были бы параллельны оси х или перпендикулярны одной из основных плоскостей проекций. Положение объекта определяют координаты х, у, z. Ориентацию объекта определяют углы α, β, g главным образом с основными плоскостями проекций.

На чертеж объекта наносят размеры его формы. На чертеже сложного объекта наносят размеры формы, положения и ориентации составляющих геометрических объектов и размеры формы всего сложного объекта.

Линейные размеры на чертежах указывают в миллиметрах без обозначения единиц измерения. При других единицах измерения длины (дюймах, сантиметрах, метрах) соответствующие размерные числа следует сопровождать обозначением единиц измерения, например, 25.0 см.

При задании всех размеров на чертеже в единой системе единиц, иной, чем миллиметры, ее следует оговорить общей надписью на поле чертежа. Угловые размеры указывают в градусах, минутах и секундах, обозначая при этом единицы измерения, например, 30° 35' 45". Размерные линии определяются границами измерения и могут иметь форму как прямой (см. рисунок 80), так и дуги окружности (рисунок 81).

Выносные линии являются вспомогательными: ими фиксируют границы измерения, между ними проводят размерные линии. Выносные линии проводят от линий видимого контура, как правило, перпендикулярно измеряемому отрезку, располагая их по возможности вне контура изображения (см. рисунок 80). Данные линии могут служить продолжением контурных линий (см. рисунок 80). Выносные линии, фиксирующие границы угла, проводят радиально от вершины измеряемого угла (см. рисунок 81).

Выносные линии выполняют на чертеже сплошными тонкими линиями толщиной 1/3 ... 1/2 от толщины контурной линии данного чертежа.

Концы выносных линий, выходящие за стрелки, на всем чертеже должны быть одинаковыми и равными 1 ... 5 мм (см. рисунок 80).

Размерную линию линейной величины следует проводить параллельно прямолинейному отрезку предмета, размер которого указывается предпочтительно, располагая его вне контура изображения (см. рисунок 80). При обозначении размера угла размерную линию проводят в виде дуги окружности с центром в вершине угла, выносными линиями служат стороны угла или их продолжение (см. рисунок 80). Размерные линии проводят на чертеже сплошными тонкими линиями толщиной 1/4 ... 1/3 от толщины контурной линии данного чертежа.

Размерные линии с обоих концов ограничивают стрелками, упирающимися остриями в соответствующие линии. Стандарт предусматривает два типа начертания стрелок, их форма показана на рисун-ке 82. Величину стрелок следует выбирать в зависимости от толщины линий видимого контура и выдерживать одинаковой для всех размеров данного чертежа. Практически можно принимать длину стрелок равной высоте цифр размерных чисел на данном чертеже. В случае пересечения стрелки близко расположенной контурной или выносной линией эти линии в месте пересечения со стрелкой должны быть прерваны (рисунок 83).

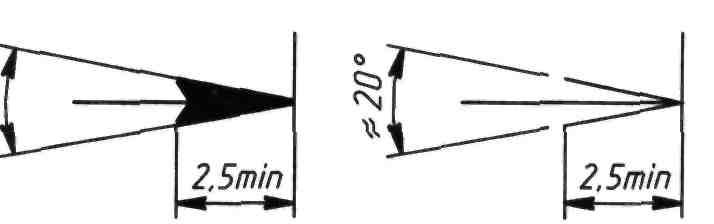
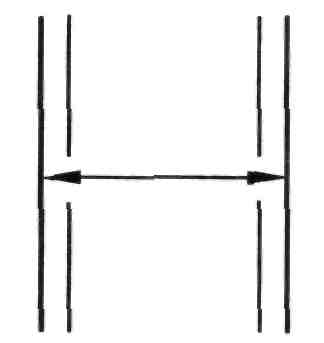
Рисунок 81 Рисунок 82 Рисунок 83

Если длина размерной линии недостаточна для размещения на ней стрелок между выносными линиями, то ее продолжают за выносные линии (контурные, осевые, центровые) и стрелки наносят снаружи выносных линий (рисунок 84).

При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допускается заменять засечками, наносимыми под углом 45° к размерным линиям (рисунок 85, а)или четко наносимыми точками (рисунок 85, б).

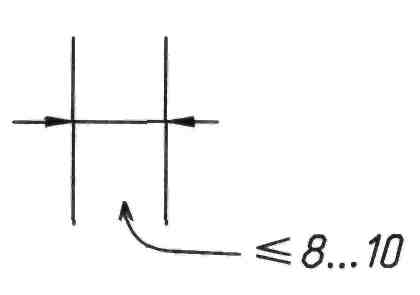
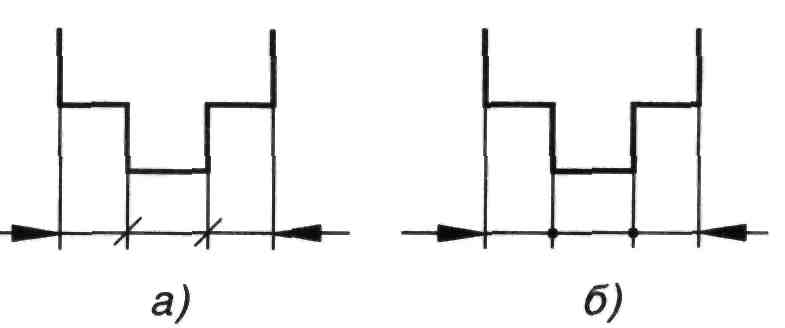
а б

Рисунок 84 Рисунок 85

Размеры в числовом выражении наносят на чертеж в их действительных значениях независимо от того, в каком масштабе и с какой точностью выполнено изображение.

Размерные числа следует наносить над размерной линией параллельно ей и возможно ближе к ее середине (см. рисунок 80). Между цифрами и размерной линией должен быть промежуток 0,5 ... 1 мм.

Чтобы исключить неправильное понимание размерных чисел, составленных из цифр 0, 6, 8, 9, следует после последней цифры ставить точку. В качестве размерных чисел применение простой дроби не допускается, за исключением относительных величин и размеров, заданных в дюймах.

В местах нанесения размерного числа следует прерывать центровую и осевую линии и линии штриховки (рисунок 86). Нельзя разрывать линию контура для размещения размерного числа. Не допускается размещать размерные числа в местах пересечения размерных, осевых и центровых линий. Недопустимо разделять или пересекать размерные числа, какими бы то ни было линиями чертежа.

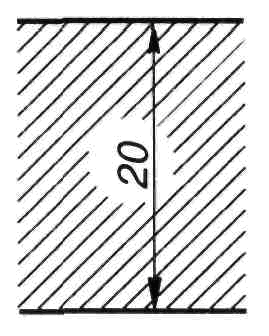
Рисунок 86

Если часть объекта изображена с отступлением от масштаба, то размерное число этой части объекта следует подчеркнуть (рисунок 87).

Размерные линии можно проводить к линиям видимого контура, осевым, центровым и выносным линиям. Предпочтительнее помещать размерную линию между выносными линиями, а не между контурными, и располагать ее вне контура изображения. Следует по возможности избегать пересечений размерных линий с размерными и выносными линиями.

Недопустимо использовать линии контура, осевые, центровые и выносные в качестве размерных. Исключением служит способ задания криволинейного контура (рисунок 88). Выносные и размерные линии, проходящие по заштрихованному полю чертежа, не должны совпадать с направлением линий штриховки. Допускается использовать на чертеже в качестве выносных осевые линии. Не рекомендуется проводить выносные линии от линий невидимого контура.

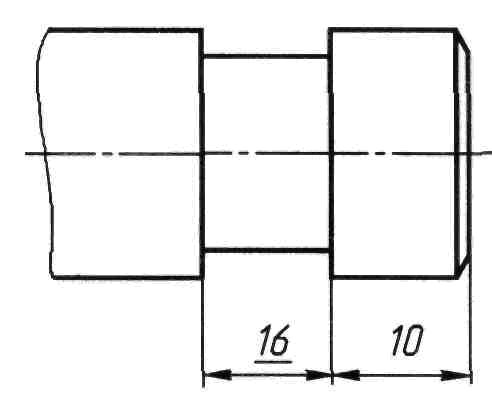
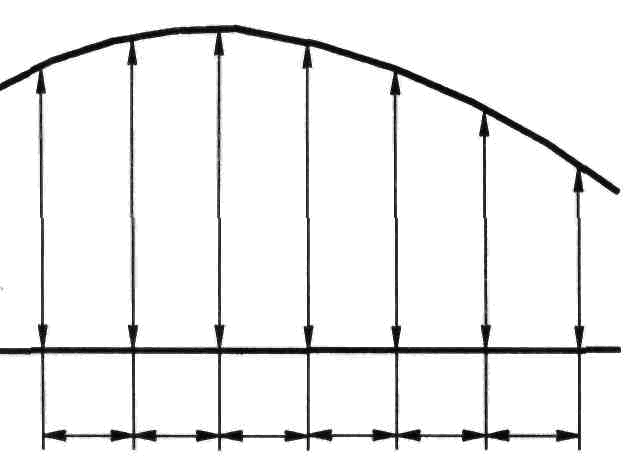
Рисунок 87 Рисунок 88

Если изображение объекта выполнено с разрывом, то размерную линию не прерывают (рисунок 89).

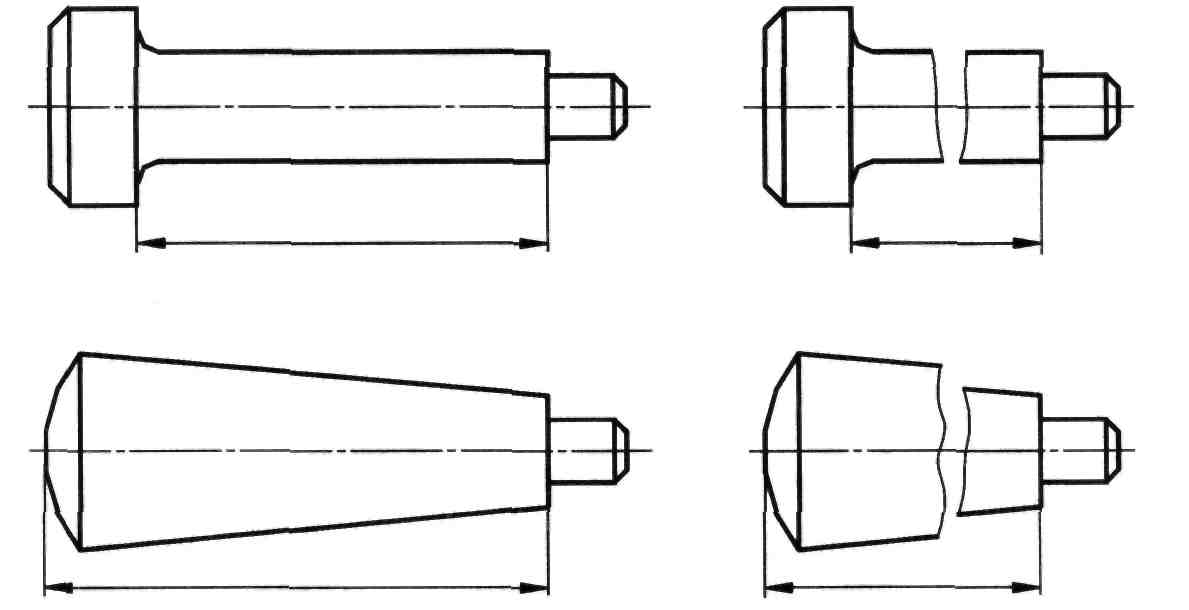
Рисунок 89

Наиболее распространенным размером является размер отрезка прямой.

При нескольких параллельных размерных линиях самый малый размер располагают ближайшим к изображению на расстоянии как минимум 10 мм от контура изображения. Следующий, больший, размер наносят на расстоянии как минимум 7 мм от первого размера; в такой последовательности и на тех же расстояниях располагают все последующие размеры (рисунок 90). Размерные числа размещают при этом над размерными линиями в шахматном порядке (рисунок 91).

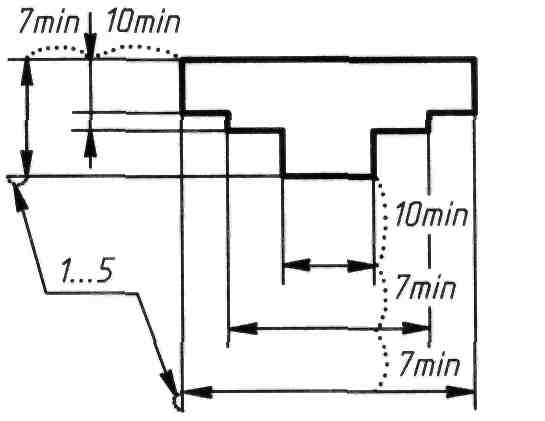
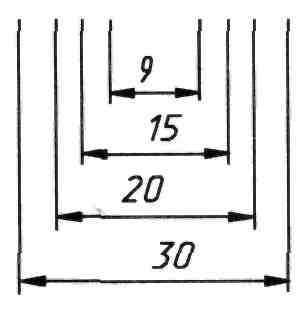
Рисунок 90 Рисунок 91

При вертикальном положении размерной линии размерные числа всегда наносят слева от размерной линии. Если размерные линии расположены наклонно, то размерные числа линейных размеров следует располагать в соответствии со схемой, приведенной на рисунке 92. При этом, если размерная линия находится в заштрихованной зоне приведенной схемы, то размерное число следует нанести на полке линии–выноски, а саму полку расположить параллельно основной надписи.

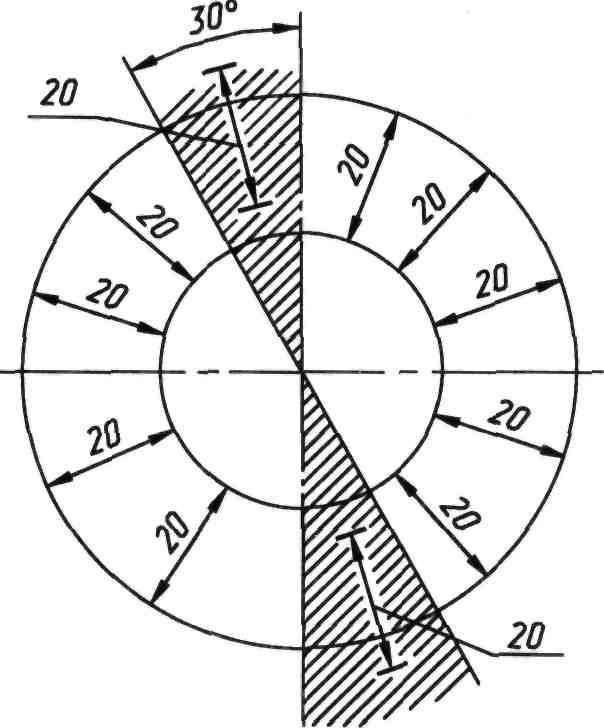
Рисунок 92

Если для нанесения размерного числа над размерной линией недостаточно места, то его следует наносить по одному из вариантов, представленных на рисунке 93. Если не хватает места для нанесения стрелок на коротких размерных линиях, то стрелки следует наносить по одному из вариантов, приведенных на рисунке 94.

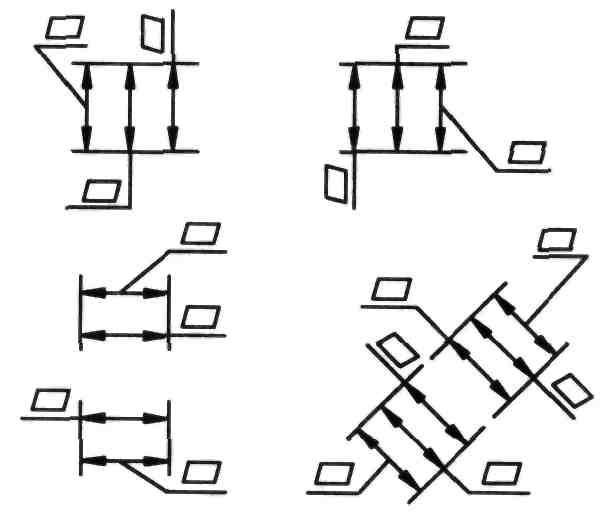
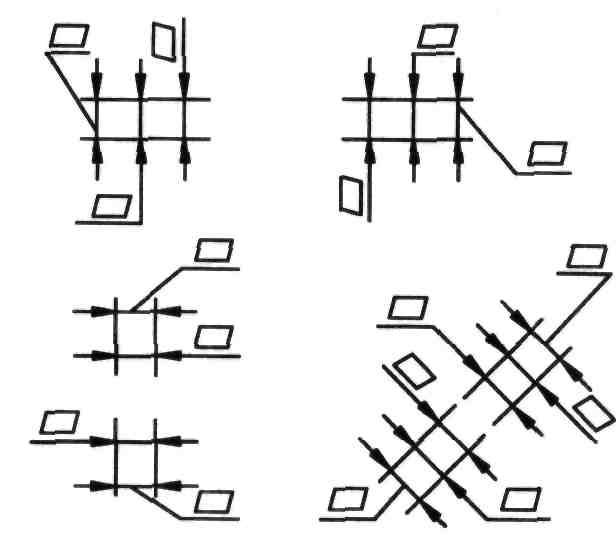
Рисунок 93 Рисунок 94

Если выносные линии сливаются с контурными линиями или близки к ним, что затрудняет понимание, однозначность задаваемого отрезка, то рекомендуется провести выносные линии под острым углом к измеряемому отрезку, а размерную линию сместить в сторону. При этом измеряемый отрезок, размерная и выносные линии образуют параллелограмм (рису- нок 95).

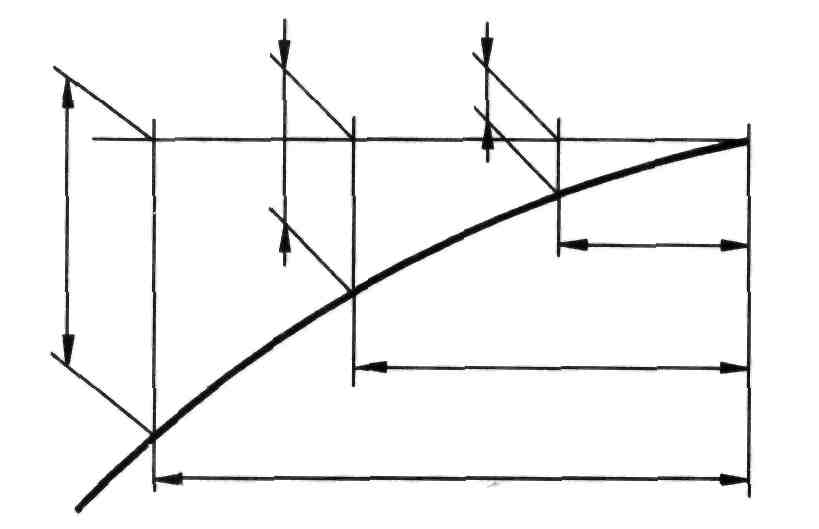
Рисунок 95

Размерную линию радиуса окружности следует проводить между дугой или ее продолжением и центром. Размерная линия радиуса имеет только одну стрелку. Радиус дуги окружности обозначают прописной буквой R, которую ставят перед размерным числом, задающим размер радиуса. Положение центра радиуса дуги изображают "крестиком" из линий толщиной от 1/3 до 1/2 толщины контурной (рисунок 96).

При задании нескольких радиусов, исходящих из одного центра, их размерные линии не должны располагаться на одной прямой (см. рису-нок 96).

В случае необходимости проведения нескольких радиусов из одного центра крайние размерные линии проводят из центра, остальные допускается не доводить до центра (рисунок 97). Размеры одинаковых радиусов можно указывать на одной общей полке (рисунок 98).

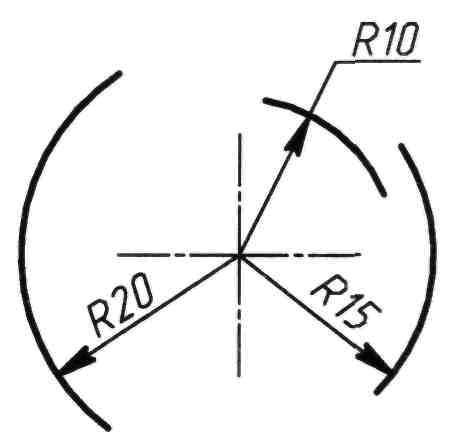
Рисунок 96

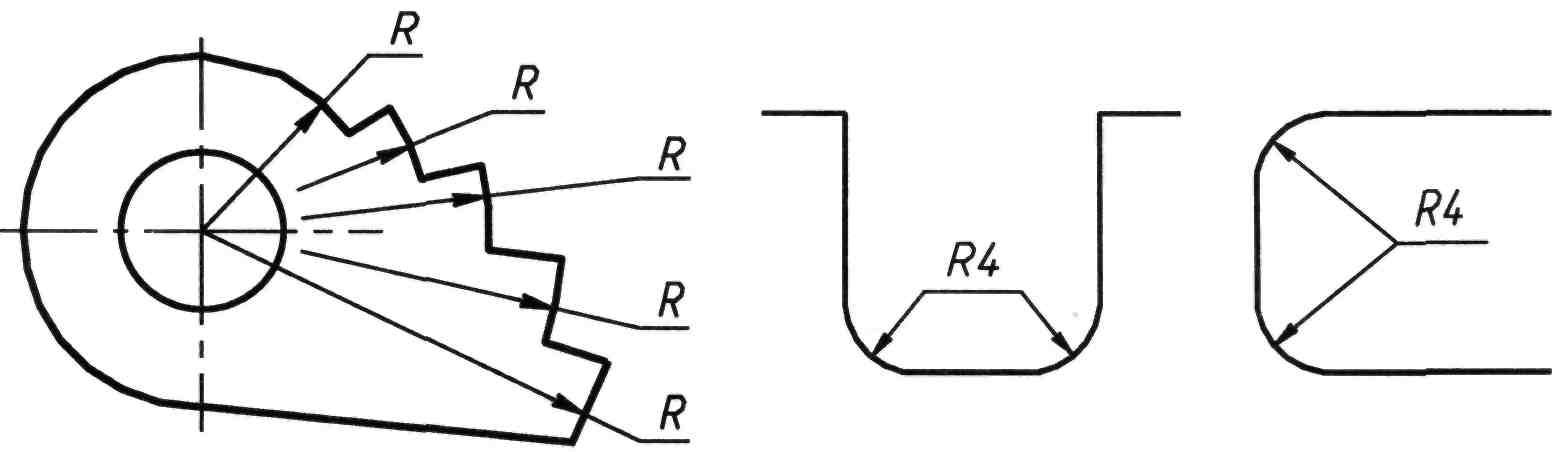
Рисунок 97 Рисунок 98

Если центр дуги окружности при большой величине ее радиуса находится вне поля чертежа, допускается центр условно приближать к задаваемой дуге. В этом случае размерную линию радиуса изображают с изломом под углом 90° и всегда направляют к центру закругления (рису- нок 99).

Если чертежный радиус дуги окружности равен 1 мм или менее, то дугу окружности не изображают, а наносят только ее размер с внешней стороны дуги (рисунок 100).

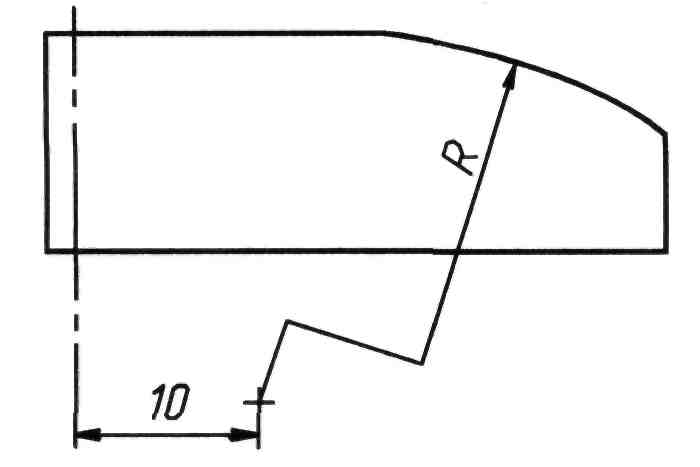
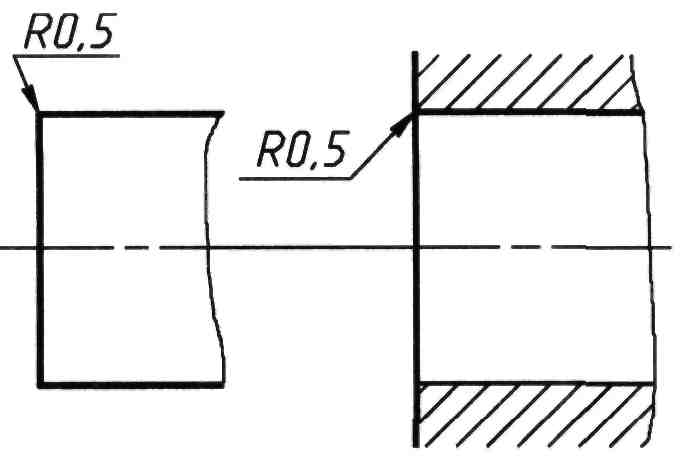
Рисунок 99 Рисунок 100

При обозначении координат вершины скругляемого угла или центра дуги скругления выносные линии проводят от точек пересечения сторон угла или от центра дуги скругления (рисунок 101).

Размеры радиусов наружных и внутренних скруглений наносят над размерной линией или на полке–выноске самой размерной линии. При этом следует избегать совпадения направления размерной линии радиуса с направлением штриховки. Вариант написания размерных чисел при различных положениях размерных линий следует выбирать, исходя из удобства их прочтения на чертеже (рисунок 102).

Если радиусы скруглений на всем чертеже одинаковы, то их можно не обозначать, а в технических требованиях сделать запись, например, такую: "Неуказанные радиусы скруглений 5 мм".

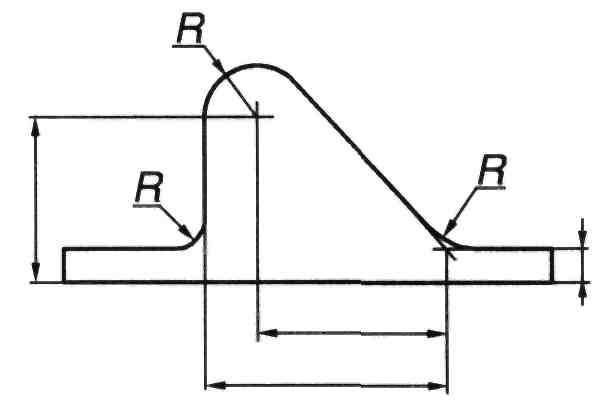
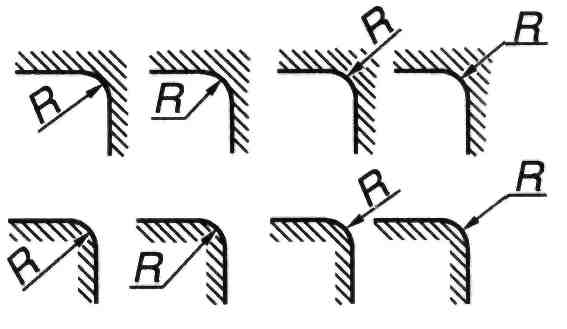
Рисунок 101 Рисунок 102

Диаметр окружности обозначают знаком ñ, который наносят перед размерным числом, задающим размер диаметра. Размерное число диаметра, расположенное внутри окружности, смещают относительно ее центра (рисунок 103).

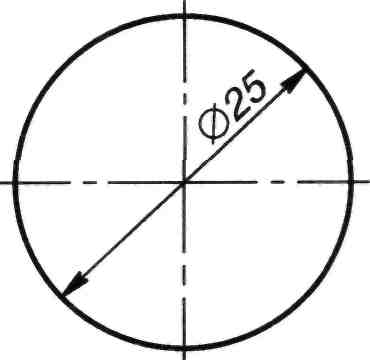
Рисунок 103

Варианты размещения размерного числа диаметра окружности:

- на продолжении размерной линии вне окружности, рисунок 104, а;

- на полке, рисунок 104, б;

- между выносными линиями на размерной линии или на ее продолжении, рисунок 104, в;

- вне выносных линий на полке линии–выноски, рисунок 104, г.

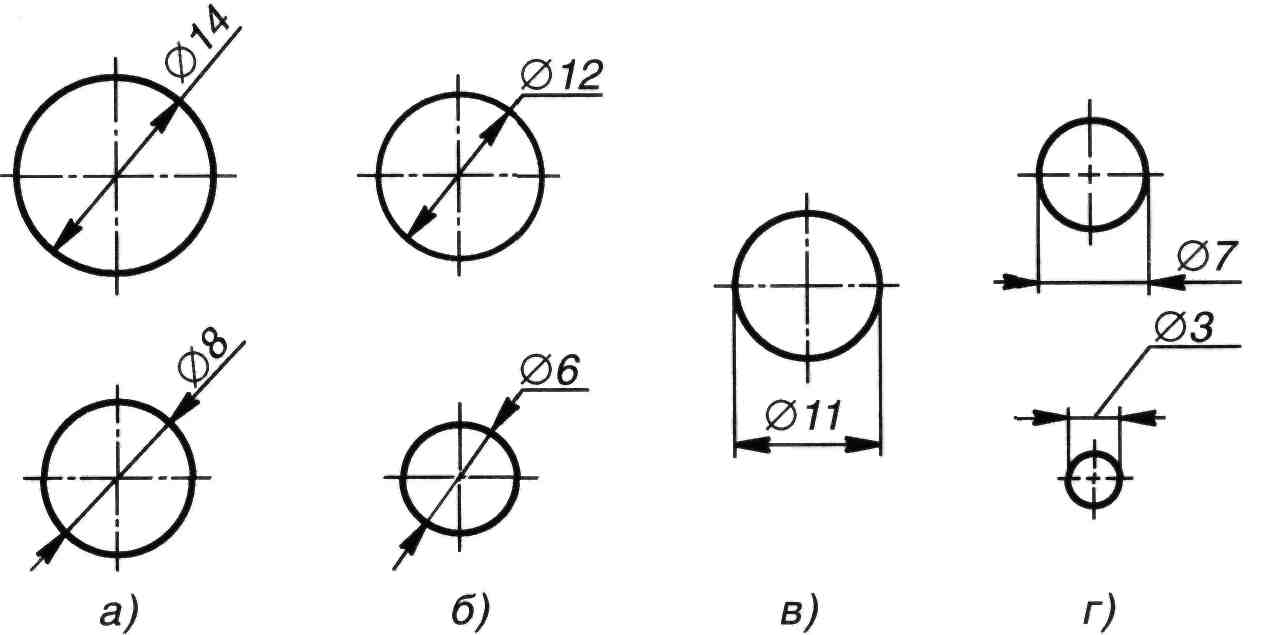
а б в г

Рисунок 104

Расположение стрелок на размерной линии диаметра:

- при чертежном диаметре, равном 12 мм и более, стрелки наносят внутри окружности или между выносными линиями;

- при чертежном диаметре, равном 12 мм и менее, стрелки наносят вне окружности или с внешней стороны выносных линий.

Размер окружности, даже прерывающейся, но имеющей противолежащие точки на диаметре, всегда следует задавать диаметром (рисунок 105).

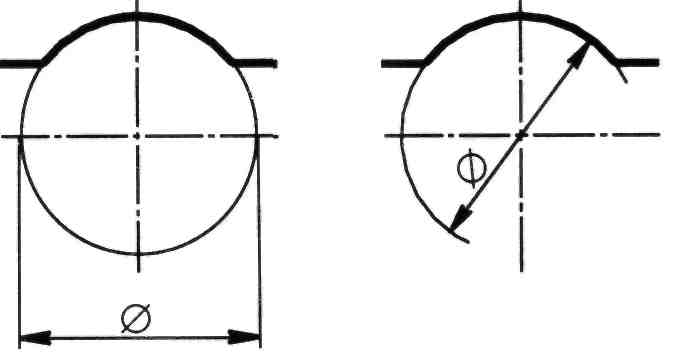
Рисунок 105

При указании диаметра окружности допускается проводить размерные линии с обрывом независимо от того, изображена окружность полностью или только ее часть, обрыв размерной линии в этом случае делают дальше центра или оси окружности (рисунок 106).

Для обозначения длины дуги окружности следует применять условный знак дуги «Þ»,который наносят над размерным числом дуги во всех случаях (рисунок 107).

Дуговую размерную линию проводят концентрично обозначаемой дуге, а выносные линии – параллельно биссектрисе угла. Если дуга охватывает большой угол, то выносные линии допускается располагать радиально, указывая при этом, к какому радиусу относится дуга (рисунок 108).

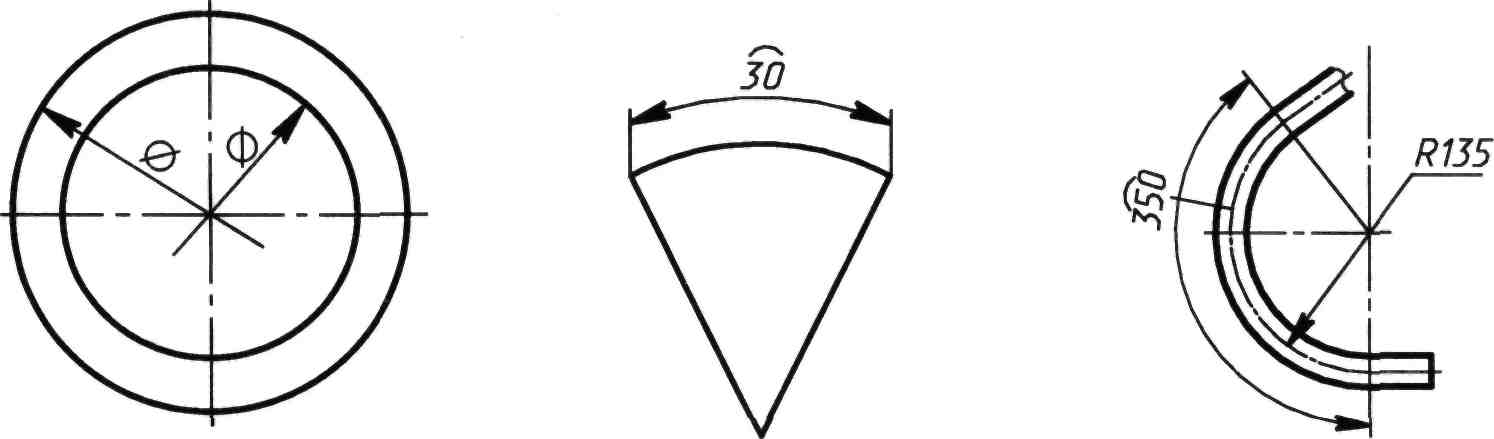
Рисунок 106 Рисунок 107 Рисунок 108

При нанесении угловых размерных линий и написании угловых размерных чисел следует руководствоваться схемой, представленной на рисунке 109. Согласно этой схеме размерные числа, расположенные выше горизонтальной осевой линии, при обозначении размера угла проставляют над размерной линией со стороны выпуклости, размерные же числа, расположенные ниже горизонтальной осевой линии, проставляют со стороны вогнутости дуговых размерных линий (см. рисунок 109). В зоне, отмеченной штриховкой на рисунке 109, размерные числа располагают на горизонтальных полках–выносках. Если при обозначении угла малого размера не хватает места для написания размерного числа, то последнее следует помещать на полке линии–выноски в любой зоне (рисунок 110).

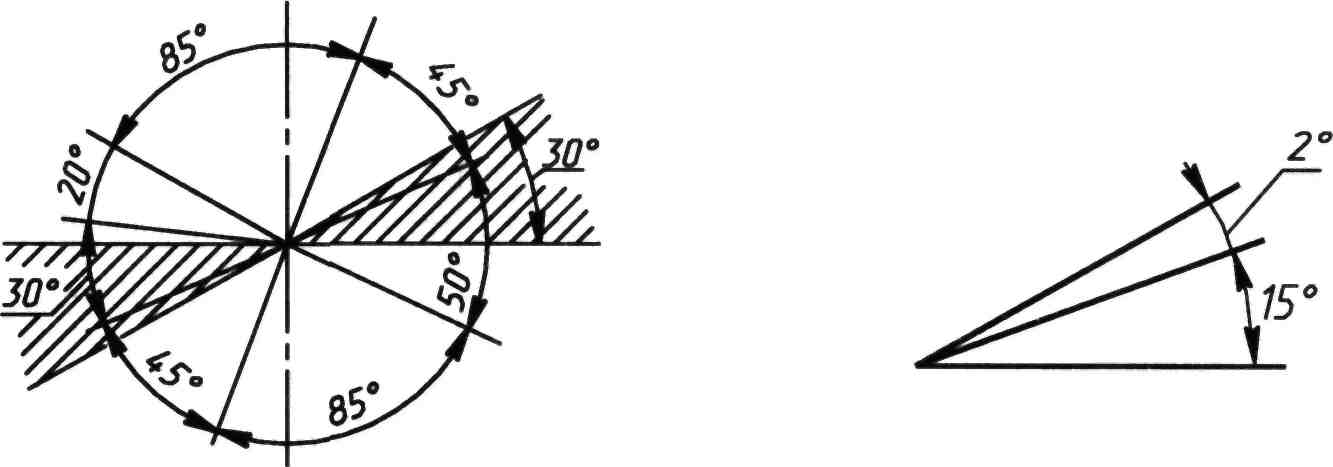
Рисунок 109 Рисунок 110

При нанесении нескольких концентрических размерных дуг (размеров углов с одной общей вершиной) размерные числа рекомендуется располагать в шахматном порядке (рисунок 111).

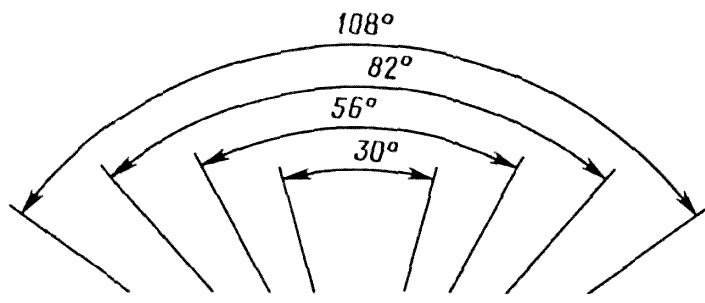
Рисунок 111

Если угол между отрезками имеет величину 0, 90, 180, 360°, то, как правило, размер угла по умолчанию не наносят.

Квадрат. Размеры квадрата наносят так, как показано на рисуноке 112. Знак □ изображают перед размерным числом. Размер знака равен высоте строчных букв.

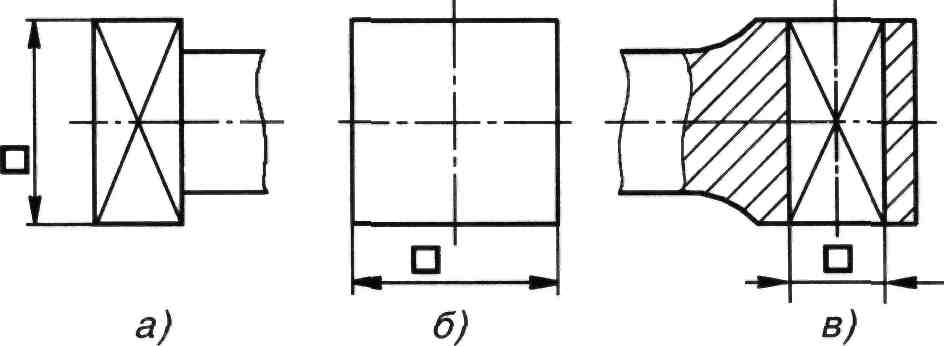
а б в

Рисунок 112

Прямоугольник. Прямоугольную форму выступа или отверстия задают двумя размерами на полке линии–выноски. При этом первый из них – размер стороны, от которой выполнена выноска, после знака х следует размер второй стороны прямоугольника (рисунок 113). Ориентация прямоугольника может быть произвольной.

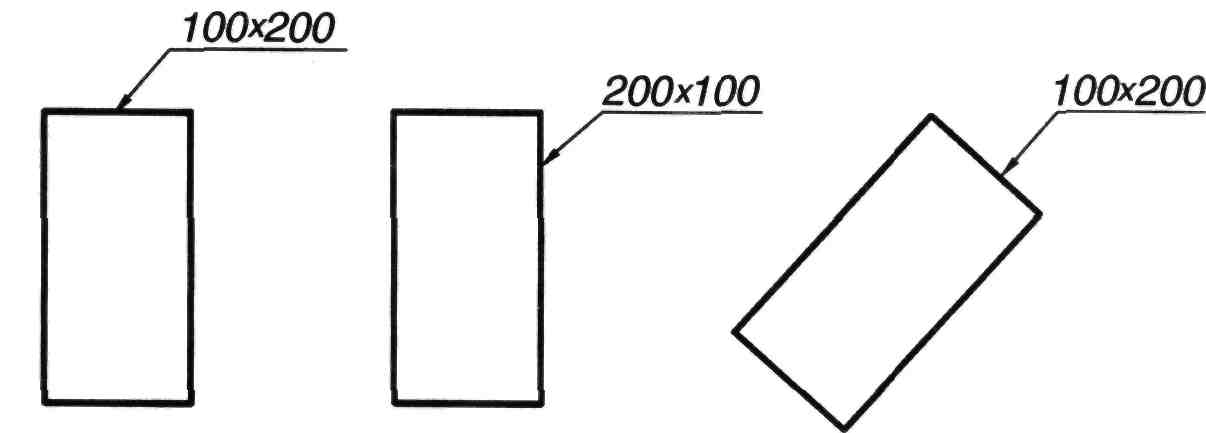
Рисунок 113

Контур шпонки и паза. Допускается на чертеже контура призматической шпонки с закругленными торцами и паза под такую шпонку нанести только два размера – длину и ширину, а величину радиуса сопрягающих окружностей не указывать (рисунок 114).

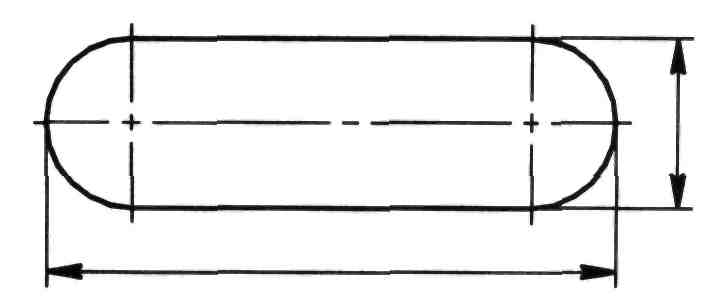
Рисунок 114

Сфера. Размер сферы задают радиусом или диаметром ñ. Если изображенную сферу (или ее фрагмент) Rтрудно отличить от других поверхностей, то перед знаком ñ или Rдопускается написать слово "Сфера" или знак Ò, высота которого равна высоте размерных чисел на чертеже (рисунок 115).

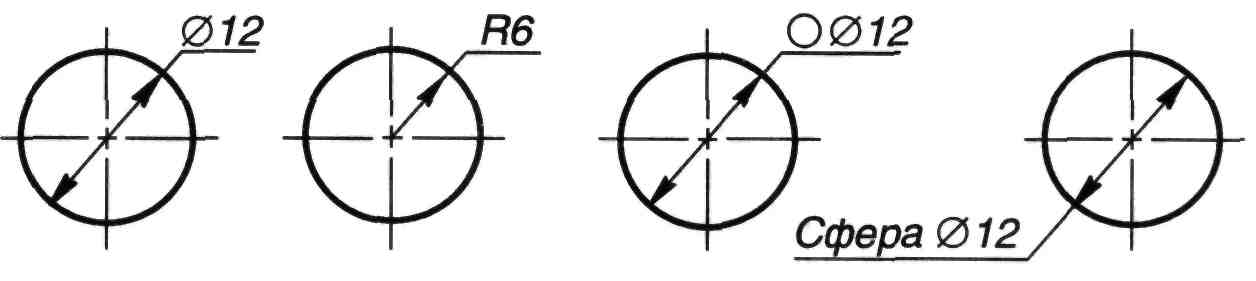
Рисунок 115

Конусность. Под конусностью понимают отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними. Перед размерным числом, определяющим конусность, наносят знак конусности – равнобедренный треугольник (рисунок 116), вершина которого должна быть направлена в сторону вершины конуса. Величина основания этого треугольника равна высоте размерных чисел чертежа. Знак конусности и ее величину в виде отношения следует наносить над осевой линией или на полке линии–выноски (рисунок 116).

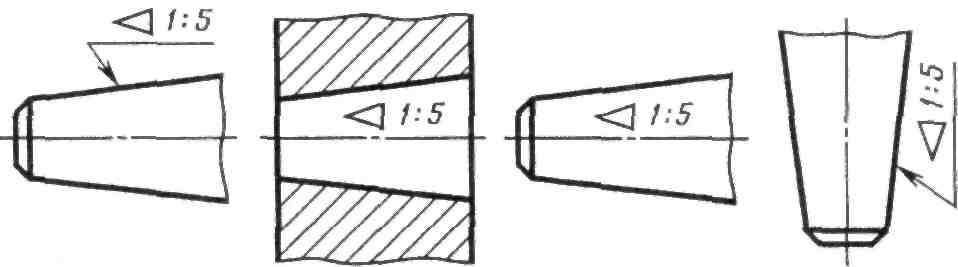
Рисунок 116

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

ОБЩИЕ ПОЛОЖЕНИЯ

ГОСТ 2.317—69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства.

Аксонометрическая проекция — один из способов изображения пространственных фигур на плоскости. Этот вид проекций обладает большой наглядностью и является обратимым изображением. Слово “аксонометрия” в переводе с греческого означает “измерение по осям”.

Сущность способа аксонометрического проецирования показана на рисунке 117: геометрическая фигура (предмет) вместе с осями прямоугольных (декартовых) координат, к которым она отнесена в пространстве, параллельно проецируется на картинную плоскость (аксонометрическую плоскость).

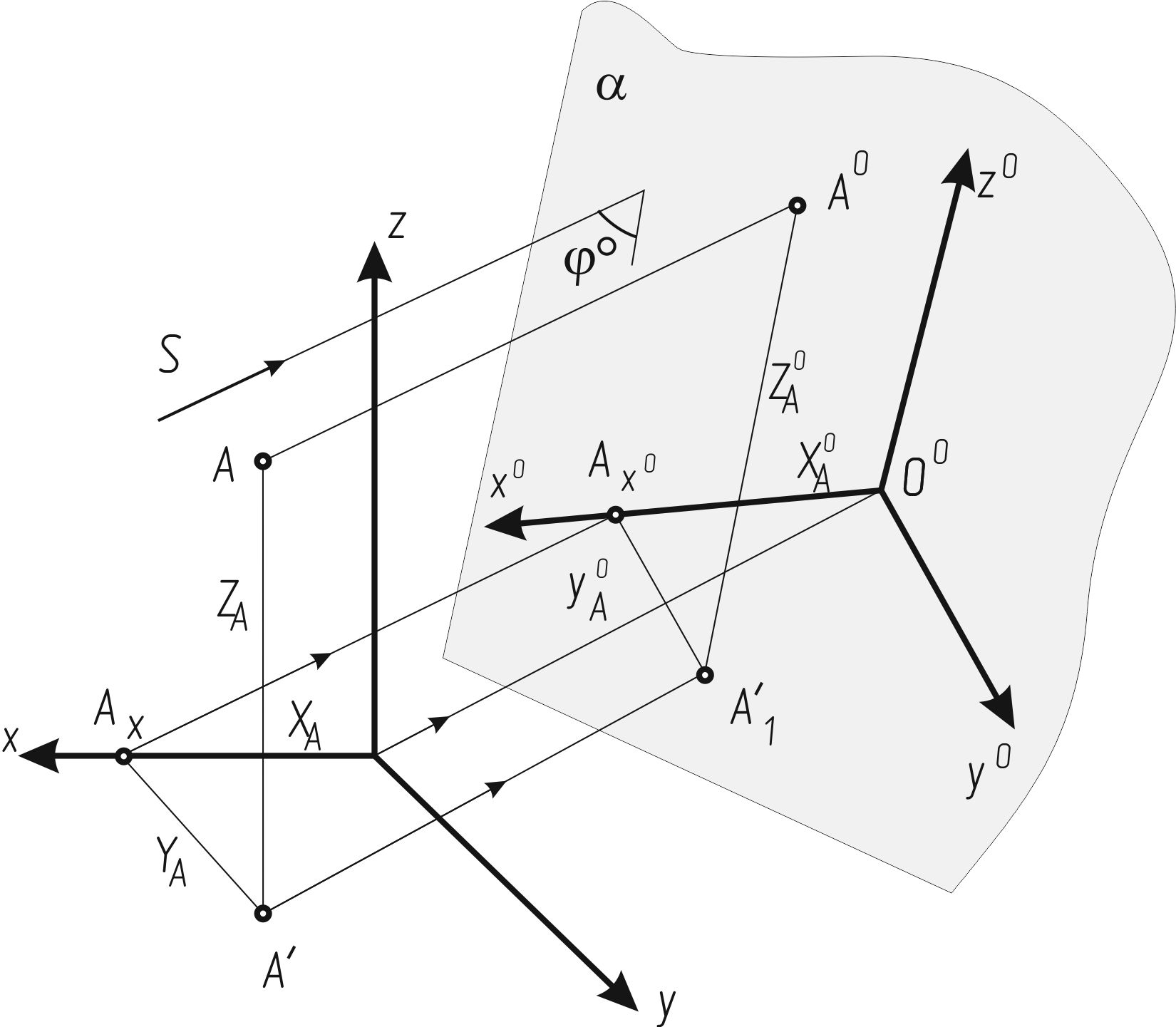
Рисунок 117

На рисунке 117 обозначено:

a — картинная (аксонометрическая) плоскость;

О_x, О_y, О_z — натуральные (декартовы) оси координат;

S — направление проецирования;

j^o — угол проецирования;

О_x, О_y, О_z — проекции натуральных осей координат на картинную плоскость — аксонометрические оси;

А^o₁ — аксонометрическая проекция точки А;

А'₁ — вторичная проекция (горизонтальная) точки А.

Для определения точки А на аксонометрической проекции (в аксонометрии) необходимо кроме аксонометрической проекции этой точки иметь ее вторичную проекцию, например, горизонтальную А₁, причем прямая А^oА'₁ должна быть параллельна аксонометрической оси z^o.

Аксонометрическая проекция точки А и ее вторичная проекция А₁ (рисунок 118) однозначно определяют положение точки в пространстве, что делает аксонометрическую проекцию обратимой. Если вторичная проекция не задана, ее можно будет задать произвольно, например, в точке А'₂ , и тогда координаты X^o_A, Y^o_A, Z^o_A изменяются.

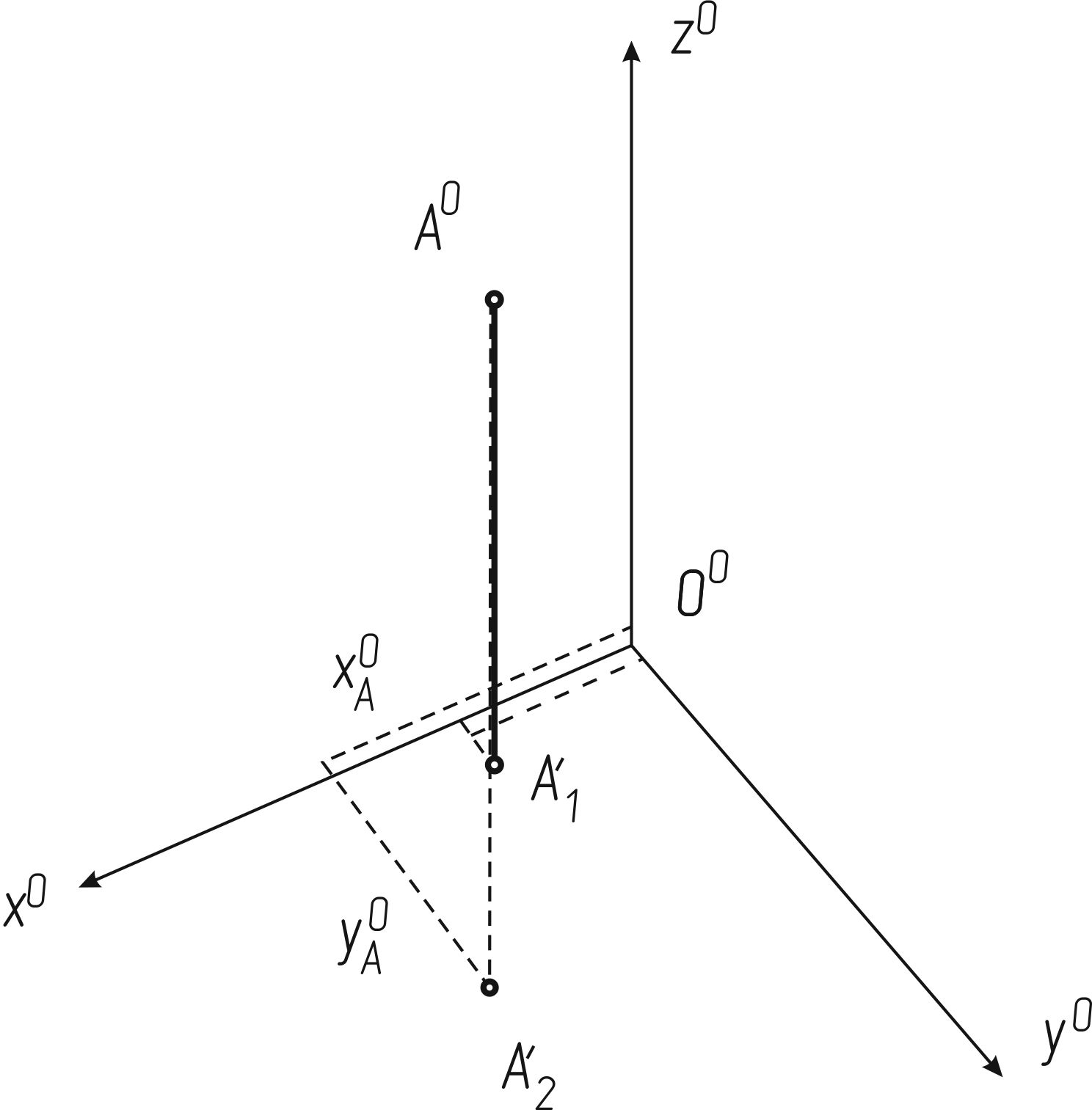
Рисунок 118

Длина отрезков натуральной координатной ломаной OA_xA'A в общем случае не равна длине их проекций О^oА^o_xА'₁А^o на картинной плоскости a (см. рисунок 117).

Искажение отрезков осей координат при их проецировании на картинную плоскость характеризуется коэффициентами искажений по аксонометрическим осям.

Коэффициентом искажения называется отношение длины аксонометрической проекции отрезка оси к его натуральной длине.

Коэффициенты искажения по осям О^oX^o , О^oY^o и О^oZ^o соответственно будут равны:

K_x = X^o_A / X_A;

K_y = Y^o_A / Y_A;

K_z = Z^o_A / Z_A.

В зависимости от направления проецирующих лучей аксонометрические проекции делятся на прямоугольные и косоугольные.

Если проецирующие прямые перпендикулярны аксонометрической плоскости проекции, то такая проекция называется прямоугольной аксонометрической проекцией. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая проекции.

Если проецирующие прямые направлены под углом к аксонометрической плоскости проекций, то получается косоугольная аксонометрическая проекция. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

Прямоугольные аксонометрические проекции дают наиболее наглядные изображения и поэтому чаще применяются в машиностроительном черчении.

ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ

Прямоугольная изометрическая проекция (рисунок 119). В прямоугольной изометрической проекции аксонометрические оси ОX, ОY и ОZ расположены под углом 120^o друг к другу, или, что удобно для вычерчивания, составляют угол 30^o с горизонтальной линией.

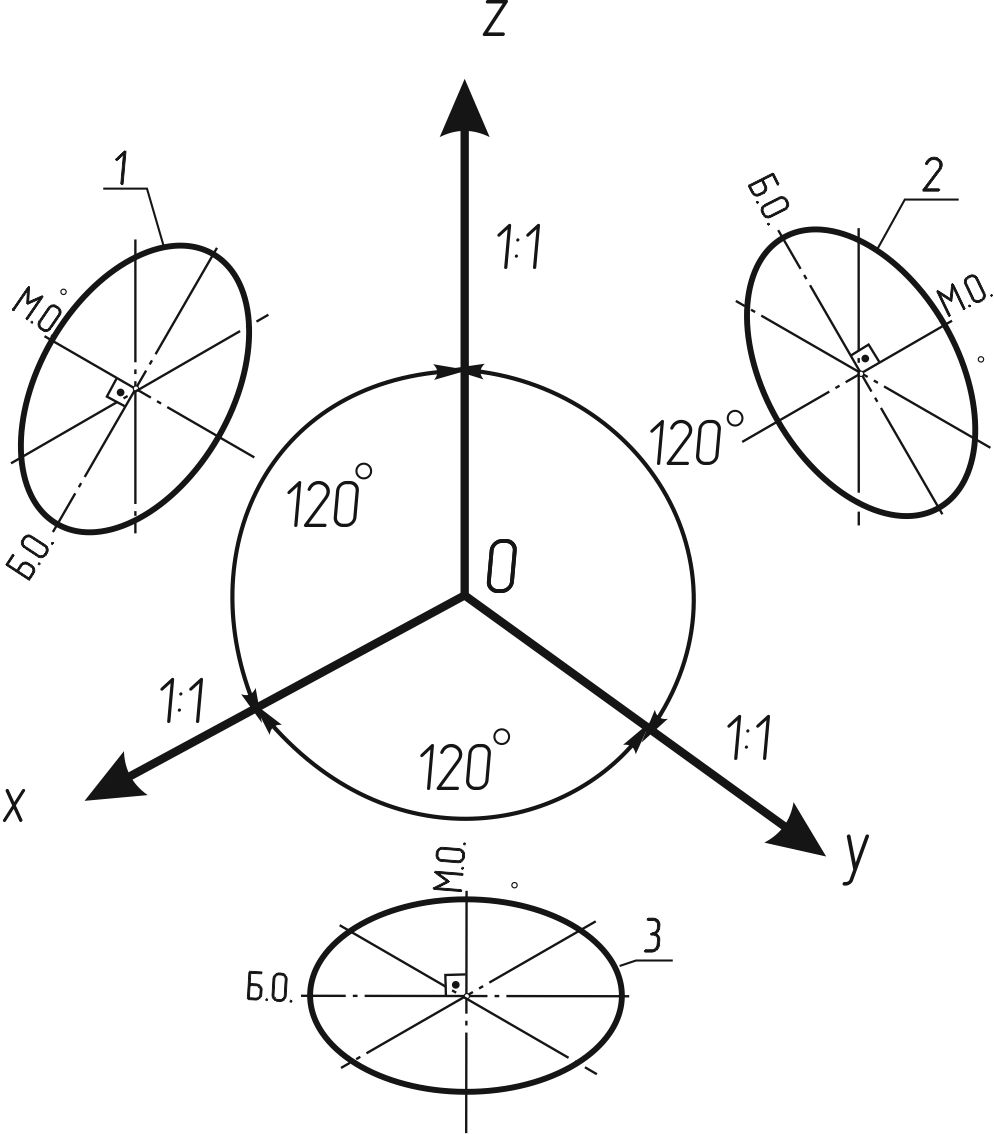
Рисунок 119

В прямоугольной аксонометрии сумма квадратов коэффициентов искажения равна двум, то есть K²_x = K²_y = K²_z = 2 .

Поэтому K_x = K_y = K_z = 0,82.

Так как эти значения неудобны для подсчета размеров при построении, то стандарт рекомендует выполнять изометрическую проекцию без искажения по осям, что соответствует замене действительных коэффициентов искажения более удобными приведенными коэффициентами, равными единице: K_x = K_y = K_z = 1. При этом изображение получается увеличенным в 1,22 раза.

Коэффициент искажения по осям OX, OY, OZ равен 0,82.

Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям OX, OY, OZ, т. е. приняв коэффициент искажения равным 1.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (рисунок 119).

Если изометрическую проекцию выполняют без искажения по осям OX, OY, OZ, то большая ось эллипсов 1, 2, 3 равна 1,22. а малая ось — 0,71 диаметра окружности.

Если изометрическую проекцию выполняют с искажением по осям OX, OY, OZ, то большая ось эллипсов (Б.О.) 1, 2, 3 равна диаметру окружности, а малая ось (М.О.) — 0,58 диаметра окружности.

Прямоугольную изометрию применяют, когда все три видимые на аксонометрическом изображении стороны предмета имеют примерно одинаковое количество особенностей, необходимых для характеристики изображаемого предмета.

Прямоугольная диметрическая проекция (рисунок 120). В прямоугольной диметрической проекции аксонометрические оси ОX и ОZ составляют между собой угол 97^o10'. Ось ОY является биссектрисой оставшегося угла, составляя с двумя другими осями равные углы 131^o25' (рисунок 11). При построении этой проекции принимают, что K_x = K_z= 0,94 и K_y=0,5K_x. =0,47.

Приведенные коэффициенты искажения будут равны: K_x= K_z = 1; K_y = 0,5, что соответствует увеличению изображения в 1,06 раза.

Окружности, лежащие и плоскостях, параллельных плоскостях проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.

Если диметрическую проекцию выполняют без искажения по осям OX и OZ то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0,95, эллипсов 2 и 3 — 0,35 диаметра окружности.

Если диметрическую проекцию выполняют с искажением по осям OX и OZ, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 — 0,9, эллипсов 2 и 3 — 0,33 диаметра окружности.

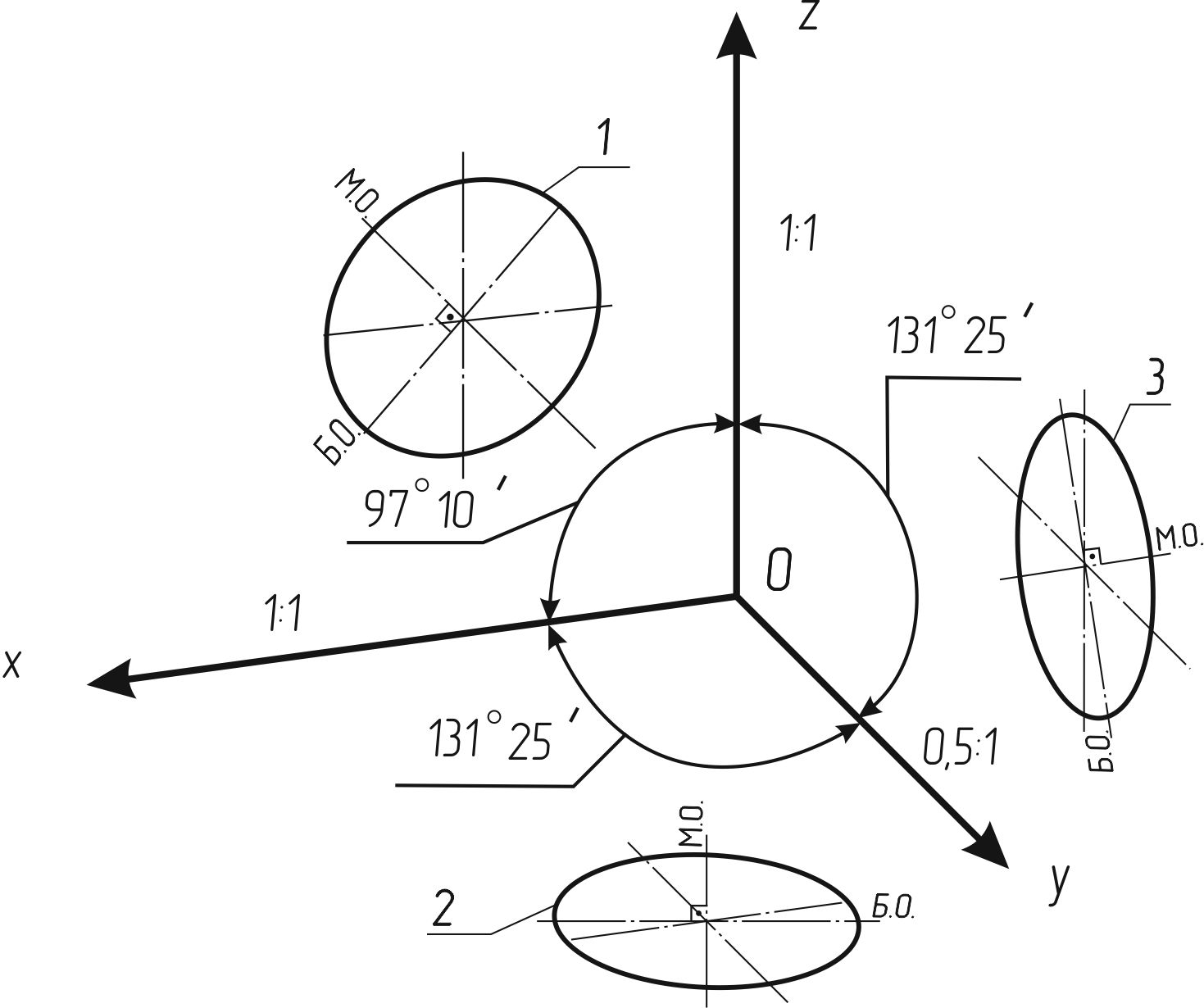
Рисунок 120

1 - эллипс (большая ось расположена под углом 90° к оси OY);

2 - эллипс (большая ось расположена под углом 90° к оси OZ);

3 - эллипс (большая ось расположена под углом 90° к оси OX)

Прямоугольная диметрия рекомендуется к применению в случае, когда наибольшее число характерных особенностей сосредоточено на одной стороне предмета. Наиболее отличающаяся особенностями сторона предмета располагается параллельно плоскости XOZ

КОСОУГОЛЬНЫЕ ПРОЕКЦИИ

Косоугольная фронтальная диметрическая проекция (рисунок 121). Аксонометрическая плоскость a располагается параллельно фронтальной плоскости проекций V. Поэтому аксонометрические оси ОX и ОZ параллельны декартовым осям ОX и ОZ.

Допускается применять фронтальные диметрические проекции с углом наклона оси OY30° и 60°

Коэффициент искажения по оси OY равен 0,5, а по осям OX и OZ — 1.

Окружности, лежащие и плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, в эллипсы (рисунок 121). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось 0,33 диаметра окружности.

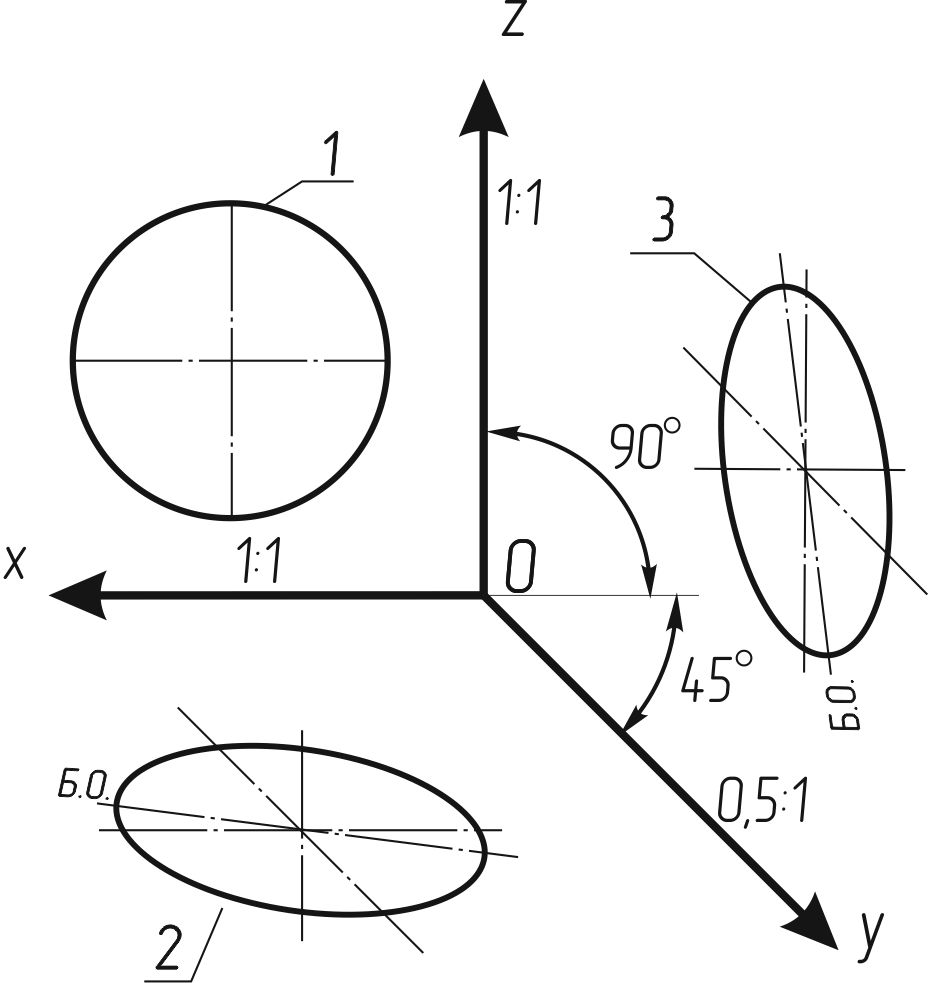
Рисунок 121

1 - окружность;

2 - эллипс (большим ось составлял с осью x угол 7°14')

3 - эллипс (большая ось составляет с осью z утл 7°14')

Косоугольная фронтальная диметрия удобна в тех случаях, когда изображаемая геометрическая фигура содержит большое число окружностей (или других кривых, состоящих из дуг окружностей), лежащих на взаимно параллельных плоскостях. При расположении этих плоскостей параллельно аксонометрической плоскости, все окружности будут проецироваться на ней также в виде окружностей, что упрощает построение.

Косоугольная фронтальная изометрическая проекция (рисунок 122). Допускается применять фронтальные изометрические проекции с углом наклона оси OY30° и 60°

Фронтальную изометрическую проекцию выполняют без искажения по осям OX, OY, OZ.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекции, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы (рисунок 122).

Большая ось эллипсов 2 и 3 равна 1,3, а малая ось 0,54 диаметра окружности.

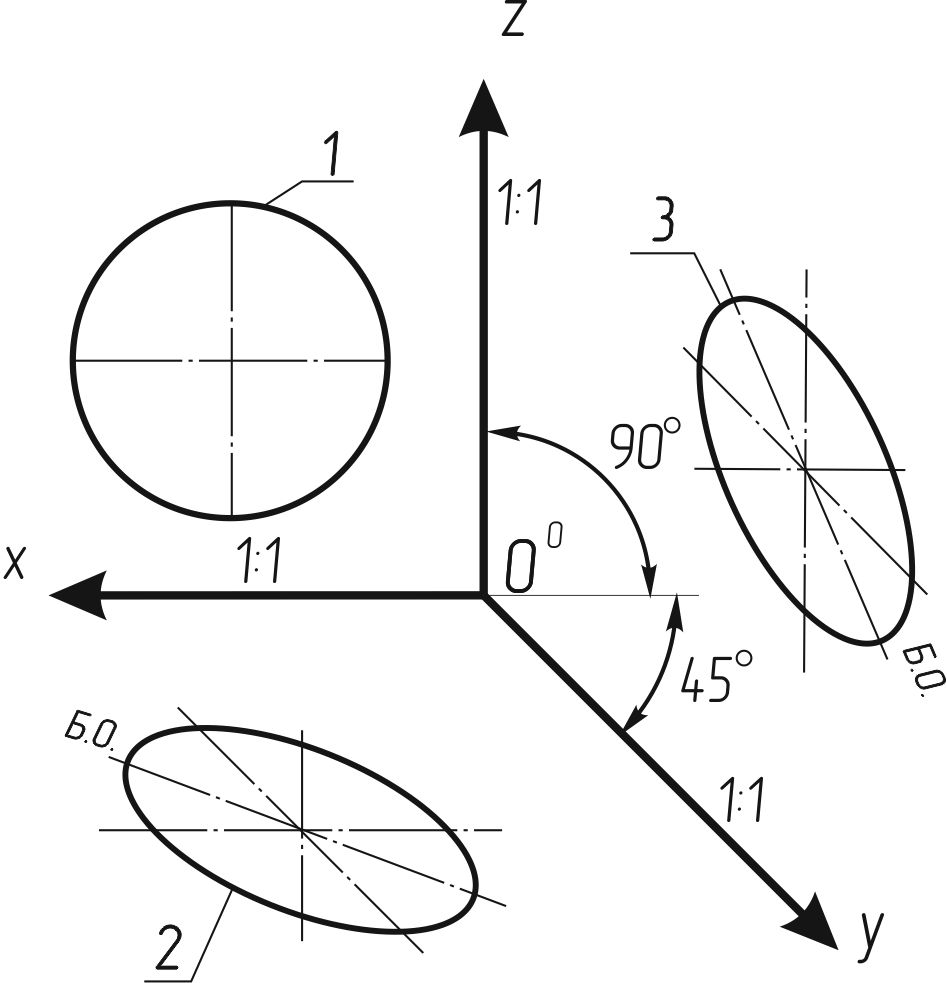
Рисунок 122

1 - окружность;

2 - эллипс (большая ось составляет с осьюOX угол 22°30');

3 - эллипс (большая ось составляет с осью OZ угол 22°30')

Косоугольная горизонтальная изометрическая проекция (рисунок 123).

Допускается применять горизонтальные изометрические проекции с углом наклона оси OY45° и 60° сохраняя угол между осями OX и OY90°

Горизонтальную изометрическую проекцию выполняют без искажения по осям OX, OY и OZ.

Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций — в эллипсы (рисунок 123).

Большая ось эллипса 1 равна 1,37, а малая ось 0,37 диаметра окружности.

Большая ось эллипса 3 равна 1,22, а малая ось — 0,71 диаметра окружности.

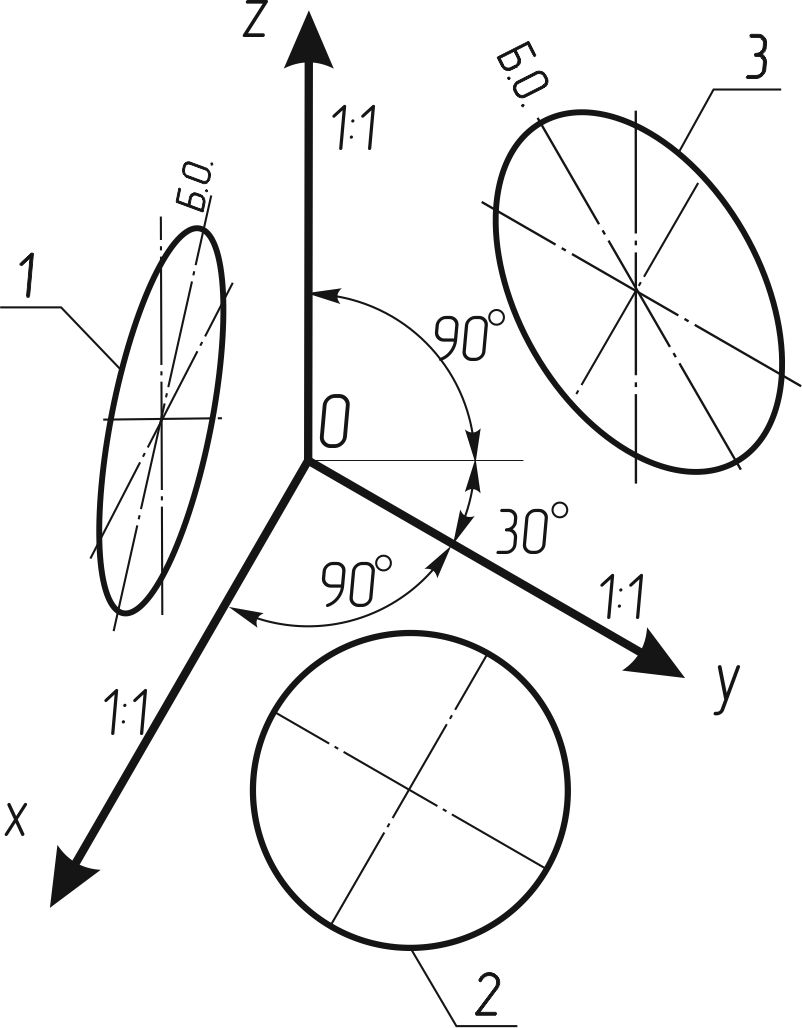
Рисунок 123

1 - эллипс (большая ось составляет с осью OZ угол 15°);

2 - окружность;

3 - эллипс (большая ось составляет с осью OZ угол 30°)