Порядок выполнения основной надписи
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
“Тульский государственный университет”
Н.Н. Бородкин, Д.В. Бескровный, Е.М. Шишмарев
Геометрические построения
Учебное пособие
Гриф
Тула 2012
Издательство ТулГУ
УДК 515(075)
Бородкин Н.Н.
Геометрические построения: учеб. пособие / Н.Н. Бородкин, Д.В. Бескровный, Е.М. Шишмарев – Тула: Изд-во ТулГУ, 2012. – 154с.
ISBN 978-5-7679-2193-5
Рассматриваются правила и стандарты для самостоятельной работы студентов технических специальностей и направлений подготовки, а также специальностей «Дизайн» и «Архитектура».
Методическое пособие поможет грамотно оформить и выполнить графическую часть в соответствии с единой системой конструкторской документации. Может быть рекомендовано студентам для самостоятельного изучения при выполнении ими графических работ и чертежей.
Табл. 5. Ил. 170. Библиогр.: 8 назв.
Печатается по решению библиотечно-издательского совета Тульского государственного университета
Рецензенты:
Независимый рецензент – зав. Кафедрой «Инженерной графики» МИРЭА, к.п.н., доцент Горшков Г.Ф.
Председатель НМС по начертательной геометрии и инженерной графике Минобрнауки РФ, Заслуженный деятель науки и техники РФ, Заслуженный работник высшей школы РФ, Почетный авиастроитель, д.т.н., профессор В.И. Якунин.
ISBN 978-5-7679-2193-5 © Н.Н. Бородкин, Д.В. Бескровный, Е.М. Шишмарев, 2012
© Издательство ТулГУ, 2012
Оглавление
Оглавление. 3
Введение. 5
1 ОСНОВНЫЕ РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ ЧЕРТЕЖА.. 6
1.1 ИНСТРУМЕНТ И МАТЕРИАЛ.. 6
1.2 ФОРМАТЫ.. 7
1.3 МАСШТАБЫ.. 7
1.4 ЛИНИИ.. 8
1.5 ШРИФТЫ ЧЕРТЕЖНЫЕ. 9
1.6 ОСНОВНАЯ НАДПИСЬ. 15
1.6.1 Порядок выполнения основной надписи. 15
1.6.2 Порядок заполнения основной надписи. 16
2 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ.. 18
2.1 ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРНЫХ И ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ 19
2.1.1 Построение перпендикулярных прямых. 19
2.1.2 Построение параллельных прямых. 21
2.2 ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ.. 22
2.2.1 Деление отрезка прямой на равные части. 22
2.2.2 Деление отрезка прямой на пропорциональные части. 23
2.3 ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ, ДЕЛЕНИЕ УГЛОВ, ПОСТРОЕНИЕ УКЛОНОВ.. 25
2.3.1 Построение и измерение углов. 25
2.3.2 Деление углов. 27
2.4 ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ, ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ.. 28
2.4.1 Деление окружности на равные части и построение правильных вписанных многоугольников. 28
2.4.2 Построение правильных многоугольников по данной стороне. 30
2.4.3 Построение правильных многоугольников, описанных около окружности 34
3 СОПРЯЖЕНИЯ.. 36
3.1 ОБЩИЕ ПОЛОЖЕНИЯ.. 36
3.2 ПОСТРОЕНИЕ КАСАТЕЛЬНЫХ И КАСАНИЕ ОКРУЖНОСТЕЙ.. 37
3.2.1 Построение касательной к окружности. 37
3.2.2 Касание окружностей. 38
3.2.3 Построение касательных к двум окружностям. 39
3.3 СОПРЯЖЕНИЯ С ПОМОЩЬЮ ДУГИ ОКРУЖНОСТИ.. 41
3.3.1 Сопряжение двух прямых дугой окружности. 41
3.3.2 Сопряжение дуги и прямой дугой окружности заданного радиуса. 42
3.3.3 Сопряжение двух дуг дугой окружности заданного радиуса. 43
3.3.4 Вычерчивание контуров деталей. 44
3.3.5 Архитектурные обломы.. 46
4 ПЛОСКИЕ КРИВЫЕ. 48
4.1 ЦИРКУЛЬНЫЕ КРИВЫЕ. 48
4.1.1 Завитки. 48
4.1.2 Коробовые кривые. 49
4.2 ЛЕКАЛЬНЫЕ КРИВЫЕ. 52
4.2.1 Порядок вычерчивания лекальных кривых. 52
4.2.2 Способы построения некоторых лекальных кривых. 53
5. НАНЕСЕНИЕ РАЗМЕРОВ.. 65
5.1 ПРАВИЛА И РЕКОМЕНДАЦИИ ПРИ ПРОСТАНОВКЕ РАЗМЕРОВ.. 65
6 АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ.. 77
6.1 ОБЩИЕ ПОЛОЖЕНИЯ.. 77
6.2 ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ.. 79
6.3 КОСОУГОЛЬНЫЕ ПРОЕКЦИИ.. 81
6.4 УСЛОВНОСТИ И НАНЕСЕНИЕ РАЗМЕРОВ.. 84
7 ГЕОМЕТРИЧЕСКИЕ ТЕЛА.. 86
7.1 ПОНЯТИЕ О ПРОСТЕЙШИХ ГЕОМЕТРИЧЕСКИХ ТЕЛАХ.. 86
7.1.1 Многогранники. 86
7.1.2 Тела вращения. 92
7.2 Комплексные чертежи группы геометрических тел. 103
8 ТЕХНИЧЕСКИЙ РИСУНОК.. 104
8.1 МЕТОДЫ ОТТЕНЕНИЙ.. 104
8.1.1 Общие понятия. 104
8.1.2 Штриховка. 105
8.1.3 Шраффировка. 109
8.1.4 Оттенение точками. 112
8.2 Рисование группы геометрических тел с оттенением. 113
8.3 ОТМЫВКА ЧЕРТЕЖЕЙ.. 113
8.3.1 Общие положения акварельной окраски. 113
9. ПОРЯДОК ВЫПОЛНЕНИЯ ГРАФИЧЕСКИХ РАБОТ. 115
9.1 ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ЗАДАНИЯ.. 115
9.1.1 Графическая работа – шрифт чертежный. 115
9.1.2 Графическая работа – деление окружности на равные части. 115
9.1.3 Графическая работа – лекальные кривые. 115
9.1.4 Графическая работа – сопряжение. 116
9.1.5 Графическая работа – комплексный чертеж группы геометрических тел 116
9.1.6 Графическая работа – технический рисунок группы геометрических тел 116
ПРИЛОЖЕНИЕ А.. 117
ПРИЛОЖЕНИЕ Б. 118
ПРИЛОЖЕНИЕ В.. 122
ПРИЛОЖЕНИЕ Г. 137
ПРИЛОЖЕНИЕ Д.. 143
ПРИЛОЖЕНИЕ Е. 153
Список использованных источников. 154
Введение
Рисунок и чертеж сопровождают нас всю жизнь, помогая разобраться в самых разнообразных вопросах науки, техники и искусства.
В давние времена у человека появилась необходимость изобразить то, что он видел, а позже то, что ему нужно было сделать. Древние графические изображения – это пещерная живопись, рисунки на камнях, папирусы, стенная живопись – постепенно совершенствовались, складывались и обобщались правила их построения.
Наряду с рисунком применялись и чертежи. В настоящее время нет такой области науки и техники, где бы ни применялись графические изображения.
Цель пособия – изучение основ геометрического черчения, позволяющего развить определенные навыки, необходимые при выполнении заданий и графических работ. Чтобы облегчить понимание излагаемого материала и сделать возможным самостоятельное изучение его, все теоретические положения и примеры иллюстрированы рисунками и чертежами.
ОСНОВНЫЕ РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ ЧЕРТЕЖА
Путем геометрических построений решают практические задачи графическим способом: все действия производятся чертежными инструментами. Результатом построения является какой-либо графический элемент: геометрическая фигура, контур детали и т.д. Для выполнения графических работ нужны следующие материалы и принадлежности: бумага, карандаши, ластик, рейсшина, угольники, линейки, лекала, циркуль. Все чертежи должны выполняться в соответствии с требованиями стандартов Единой системы конструкторской документации (ЕСКД), отличаться четким и аккуратным оформлением.
Приступая к выполнению чертежа, следует предварительно установить: размеры листа бумаги (формат чертежа); расположение изображений на листе; размещение надписей.
ИНСТРУМЕНТ И МАТЕРИАЛ
Карандаши чертежные. Для чертежных работ применяются различной твердости чертежные карандаши. Наша промышленность выпускает чертежные карандаши марок «конструктор», «топограф», «картограф» четырнадцати степеней твердости: от 7Т до 2Т – твердые; Т, ТМ, М – промежуточные; от 2М до 6М – мягкие. Твердость и мягкость зарубежных карандашей («ролло», «Кох и нор» и др.) обозначены латинскими буквами Н и В: твердые – от 9Н до 2Н; мягкие – от 2В до 6В и Н, НВ, В – промежуточные.
Для чертежных работ применяются карандаши 5Т, 4Т до М–2М или им соответствующие карандаши иностранных марок. Более мягкими делают предварительные построения. Линии наносят с очень легким нажимом, чтобы впоследствии их можно было легко стереть.
Очинять карандаш следует на правильный конус длиной около 3 см с конца, свободного от фабричного клейма и обозначения твердости. Правильно очинённый карандаш способствует точному построению чертежа. Иногда графит затачивают в виде лопаточки и острым ее углом прочерчивают линии по линейке. Для подтачивания графита во время работы применяют наждачную бумагу (среднезернистую или мелкозернистую), наклеенную на фанерную или картонную пластинку для удобства.
В циркуль обычно вставляют стержень, у которого твердость графита на номер меньше, чем принята для обводки без циркуля. Затачивать стержень можно также в виде одностороннего плоского среза или конуса. Из наконечника стержень должен выступать на 6 – 8 мм. При работе надо следить, чтобы игла и графитный стержень были на одном уровне.
Чертежная бумага должна обладать прочностью, белизной и специальной способностью выдерживать многократное нанесение и стирание линий, а также равно воспринимать тушь и акварельные краски. От чертежной бумаги требуется минимальная линейная деформация при ее смачивании и последующем высушивании.
ФОРМАТЫ
Чертежи выполняются на листах размерами, установленными ГОСТ 2. 301-68. Форматы чертежей, определяемые шириной и длиной листа, подразделяются на основные и дополнительные.
Форматы листов устанавливаются размерами внешней рамки (выполненной тонкой линией) оригиналов, подлинников, дубликатов, копий.
Формат с размерами сторон 1189 × 841 мм, площадь которого равна 1 м2, и другие форматы, полученные путем последовательного деления его на две равные части параллельно меньшей стороне соответствующего формата, принимаются за основные.
Обозначения и размеры сторон основных форматов должны соответствовать указанным в таблице 1.
Таблица 1 - Основные форматы
| Обозначение формата | Размеры сторон формата, мм |
| А0 А1 А2 А3 А4 | 841 × 1189 594 × 841 420 × 594 297 × 420 210 × 297 |
При необходимости можно применять формат А5 с размерами сторон 148 × 210 мм.
Допускается применение дополнительных форматов, образуемых увеличением коротких сторон основных форматов на величину, кратную их размерам.
МАСШТАБЫ
При выполнении чертежей принимаются масштабы изображений, установленные ГОСТ 2.302-68.
Масштабы изображений на чертежах должны выбираться из следующего ряда (таблица 2):
Таблица 2 - Масштабы изображений
| Масштабы уменьшения | 1:2; 1:2;5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200 |
| Натуральная величина | 1: 1 |
| Масштабы увеличения | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
ЛИНИИ
Чтобы чертеж был выразительным и легко читался, он должен быть оформлен линиями различной толщины и формы. Линии чертежа должны иметь начертание в соответствии с их назначением по ГОСТ 2.303-68.
Государственным стандартом установлены следующие линии и их назначение (таблица 3).
Толщина сплошной основной линии s должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения, а также от формата чертежа.
Толщина линий одного и того же типа должна быть одинакова для всех изображений на данном чертеже, вычерчиваемых в одинаковом масштабе.
Таблица 3 - Линии чертежа
| Наименование | Начертание | Толщина линии по отношению к толщине основной линии | Основное назначение |
| 1 Сплошная толстая основная | 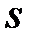 | Линии видимого контура Линии перехода видимые Линии контура сечения (вынесенного и входящего в состав разреза) | |
| 2 Сплошная тонкая | От  до до 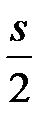 | Линии контура наложенного сечения Линии размерные и выносные Линии штриховки Линии–выноски Полки линий–выносок и подчеркивание надписей Линии для изображения пограничных деталей («обстановка») Линии для ограничения выносных элементов на видах разрезах и сечениях Линии перехода воображаемые Следы плоскостей, линии построения характерных точек при специальных построениях | |
| 3 Сплошная волнистая | От 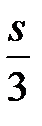 до до 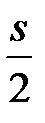 | Линии обрыва Линии разграничения вида и разреза | |
| 4 Штриховая | 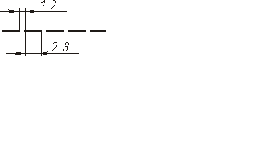 | От 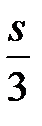 до до 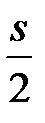 | Линии невидимого контура Линии перехода невидимые |
| 5 Штрихпунктирная тонкая | 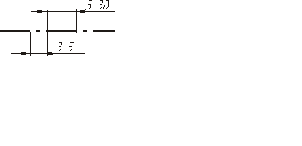 | От 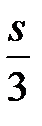 до до 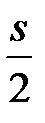 | Линии осевые и центровые Линии сечений, являющиеся осями для наложенных или вынесенных сечений |
| 6 Сплошная тонкая с изломами |  | От 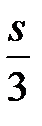 до до 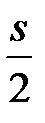 | Длинные линии обрыва |
ШРИФТЫ ЧЕРТЕЖНЫЕ
Все надписи на чертежах должны быть выполнены чертежным шрифтом.
ГОСТ 2.304-81 устанавливает два типа шрифта: тип А и тип Б, с наклоном и без наклона. В настоящем пособии подробно рассмотрен шрифт тип А с наклоном 75° и параметрами, приведенными в таблице 4.
Размер шрифта h – величина, определенная высотой прописных букв в миллиметрах.
Высота прописных букв h измеряется перпендикулярно к основанию строки. Высота строчных букв c определяется из отношения их высоты (без отростков k) к размеру шрифта h, например, с = 7/10h (рисунки 1 и 2)
Ширина буквы g –наибольшая ширина буквы, измеренная в соответствии с рисунками 1 и 2, определяется по отношению к размеру шрифта h, например, g=6/10h, или по отношению к толщине линии шрифта d, например, g = 6d.
Толщина линии шрифта d – толщина, определяемая в зависимости от типа и высоты шрифта.

Рисунок 1
Вспомогательная сетка – сетка образованная вспомогательными линиями, в которые вписываются буквы. Шаг вспомогательных линий сетки определяется в зависимости от толщины линии шрифта d (рисунок 2).
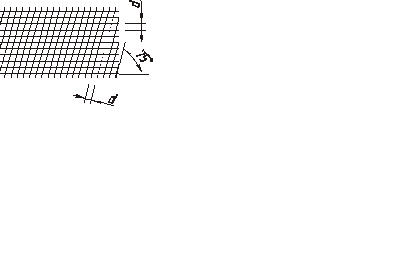
Рисунок 2
Таблица 4 - Шрифт типа А (d= h/14) с наклоном
| Параметры шрифта | Обозначение | Относительный размер | Размер, мм | |||||||
| Размер шрифта, высота прописных букв | h | (14/14) h | 14 d | 2,5 | 3,5 | 5,0 | 7,0 | 10,0 | 14,0 | 20,0 |
| Высота строчных букв | с | (10/14)h | 10 d | 1,8 | 2,5 | 3,5 | 5,0 | 7,0 | 10,0 | 14,0 |
| Расстояние между буквами | а | (2/14) h | 2 d | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 | 2,0 | 2,8 |
| Минимальный шаг строк (высота вспомогательной сетки) | b | (22/14) h | 22 d | 4,0 | 5,5 | 8,0 | 11,0 | 16,0 | 22,0 | 31,0 |
| Минимальное расстояние между словами | е | (6/14) h | 6 d | 1,1 | 1,5 | 2,1 | 3,0 | 4,2 | 6,0 | 8,4 |
| Толщина линии шрифта | d | (1/14) h | d | 0,18 | 0,25 | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 |
Примечания:
1 Расстояние a между буквами, соседние линии которых не параллельны между собой (например, ГА, АТ), может быть уменьшено наполовину, т.е. на толщину d линии шрифта.
2 Минимальным расстоянием между словами е, разделенными знаками препинания, является расстояние между знаком препинания и следующим за ним словом.
3 Устанавливаются следующие размеры шрифта: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.
4 Предельные отклонения размеров букв и цифр +0,5 мм.
Начертание букв и символов приведены на рисунках 3, 4, 5, 6, 7.
РУССКИЙ АЛФАВИТ (КИРИЛЛИЦА)

Рисунок 3
ЛАТИНСКИЙ АЛФАВИТ

Рисунок 4
АРАБСКИЕ И РИМСКИЕ ЦИФРЫ
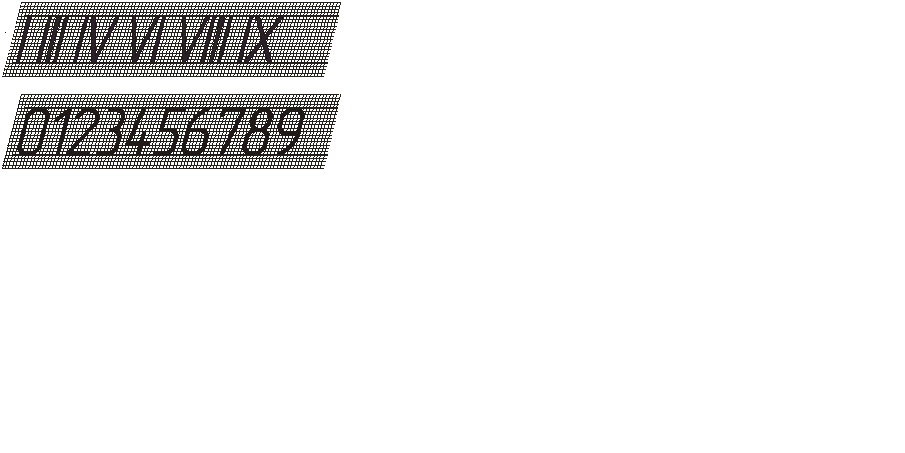
Рисунок 5
ГРЕЧЕСКИЙ АЛФАВИТ

Рисунок 6
| Наименование букв греческого алфавита, приведенных на рисунке 6 : | ||
| 1 – альфа | 9 – йота | 17 – ро |
| 2 – бета | 10 – каппа | 18 – сигма |
| 3 – гамма | 11 – ламбда | 19 – тау |
| 4 – дельта | 12 – мю | 20 – ипсилон |
| 5 – эпсилон | 13 – ню | 21 – фи |
| 6 – дзета | 14 – кси | 22 – хи |
| 7 – эта | 15 – омикрон | 23 – пси |
| 8 – тэта | 16 – пи | 24 – омега |
ЗНАКИ
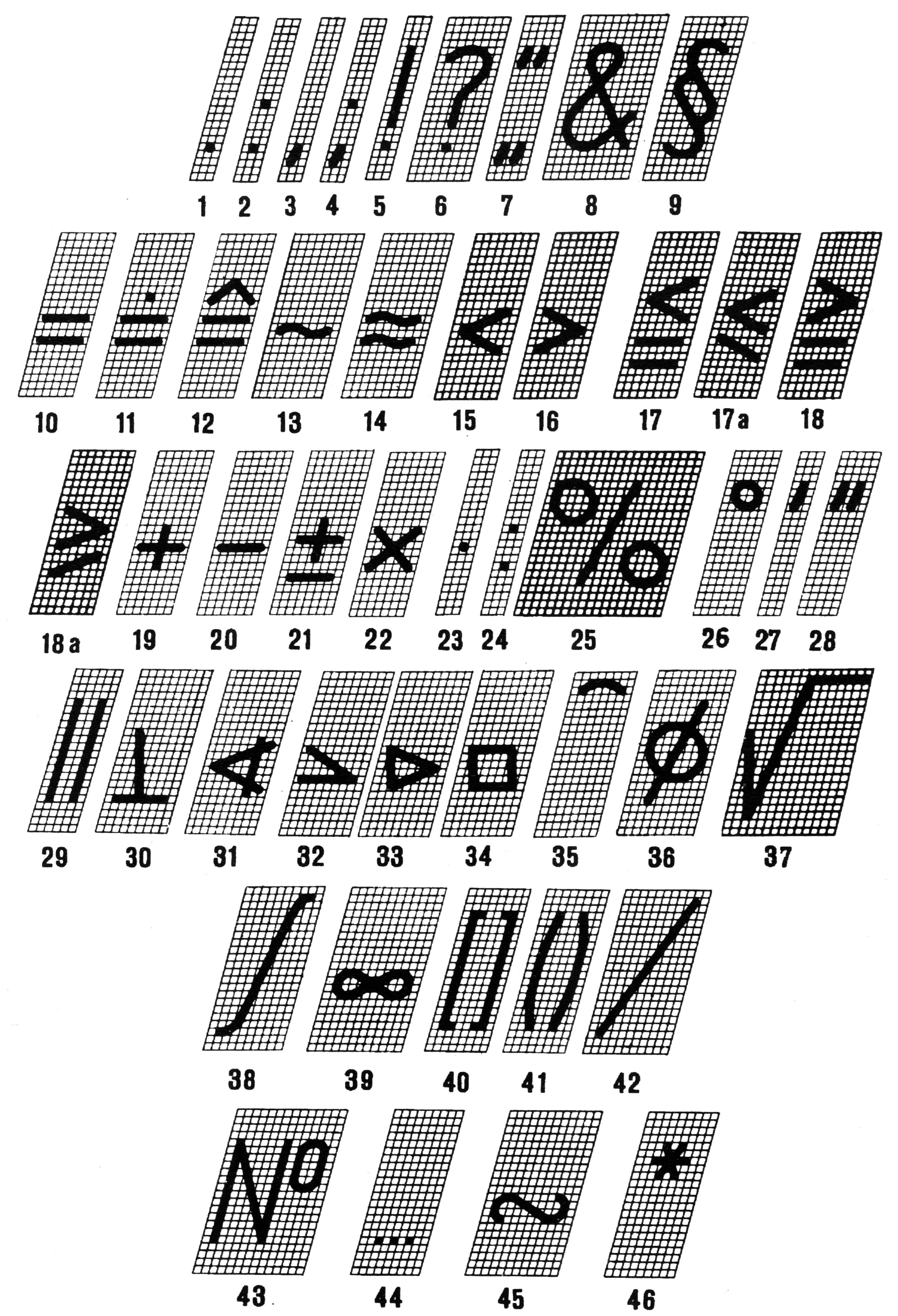
Рисунок 7
Наименования знаков приведены в таблице 5.
Таблица 5 - Наименования знаков
| Номера знаков на чертежах | Наименование знака | Номера знаков | Наименование знака |
| Точка | Процент | ||
| Двоеточие | Градус | ||
| Запятая | Минута | ||
| Точка с запятой | Секунда | ||
| Восклицательный знак | Параллельно | ||
| Вопросительный знак | Перпендикулярно | ||
| Кавычки | Угол | ||
| И | Уклон | ||
| Параграф | Конусность | ||
| Равенство | Квадрат | ||
| Величина после округления | Дуга | ||
| Соответствует | Диаметр | ||
| Асимптотически равно | Радикал | ||
| Приблизительно равно | Интеграл | ||
| Меньше | Бесконечность | ||
| Больше | Квадратные скобки | ||
| 17 и 17а | Меньше или равно | Круглые скобки | |
| 18 и 18а | Больше или равно | Черта дроби | |
| Плюс | Номер | ||
| Минус тире | От до | ||
| Плюс – минус | Знак подобия | ||
| 22 23 | Умножение | Звездочка | |
| Деление |
ОСНОВНАЯ НАДПИСЬ
Чертежи сопровождаются основной надписью по ГОСТ 2.104-2006, которую располагают в его правом нижнем углу.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
Под геометрическими построениями понимают элементарные построения на плоскости, основанные на основных положениях геометрии. К ним относятся: проведение взаимно перпендикулярных и параллельных прямых, деление отрезков, углов и др. Геометрические построения выполняют циркулем и линейкой (рейсшиной) или линейкой и угольником. Знание геометрических построений позволяет правильно начертить контур любого изделия, точно выполнить рамку формата чертежа и верно расположить чертеж внутри ее, точно разметить надписи. Таким образом, геометрические построения являются основой для выполнения чертежа. Знание их значительно ускоряет выполнение чертежа, так как позволяет в каждом случае выбрать наиболее рациональные приемы построений. Кроме того, выполнение геометрических построений дает возможность овладеть правильными приемами работы чертежными инструментами.
Графические построения всегда неточны, но степень неточности может быть различной. Построение более точно, если оно содержит мало операций (под операцией понимают проведение прямой линии, вычерчивание дуги, откладывание отрезка и т. п.). Поэтому при решении задачи на построение очень важно выбрать наиболее короткий путь.
Точность геометрических построений во многом зависит от аккуратности и внимания работающего. При этом необходимо иметь в виду следующее:
1. Проводимые линии должны быть тонкими и чертить их надо твердым карандашом.
2. Точку на чертеже следует задавать как точку пересечения двух линий: двух прямых, двух дуг или прямой и дуги. Во всех случаях нужно стремиться к тому, чтобы угол между этими линиями был прямым или приближался к нему (рисунок 11).

Рисунок 11
3. Проводя прямую через две точки, желательно брать их подальше друг от друга, так как при сближении точек увеличивается возможность отклонения прямой от ее истинного направления (рисунок 12).
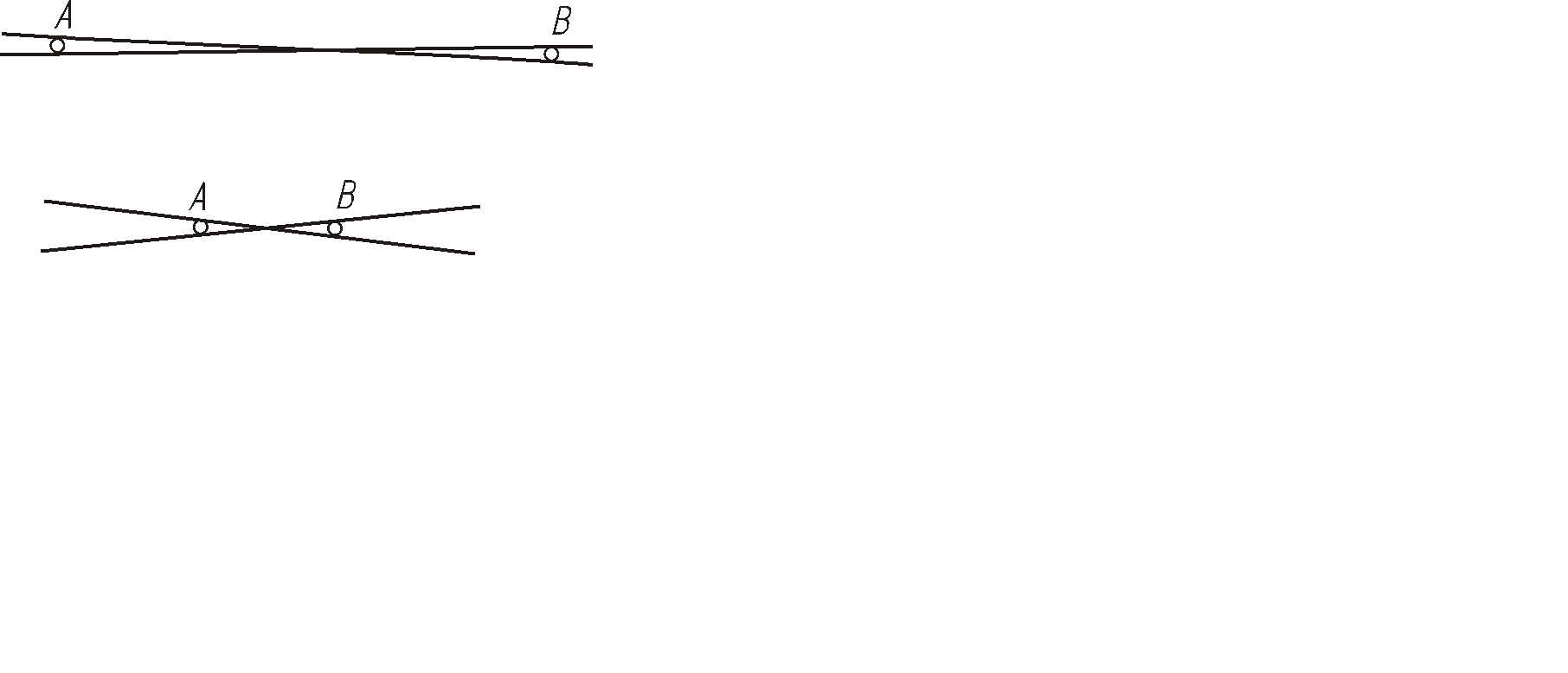
Рисунок 12
ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ
Деление углов
Деление угла пополам (рисунок 26, а). Из вершины В угла ABC произвольным радиусом R1 проводят дугу до пересечения ее со сторонами угла в точках М и N. Затем из точек M и N проводят дуги радиусом >R1 до взаимного пересечения их в точке D. Прямая BD разделит данный угол пополам.
Деление угла на 4, 8 и т. д. равных частей осуществляется последовательным делением пополам каждой части угла (рисунок 26, б).
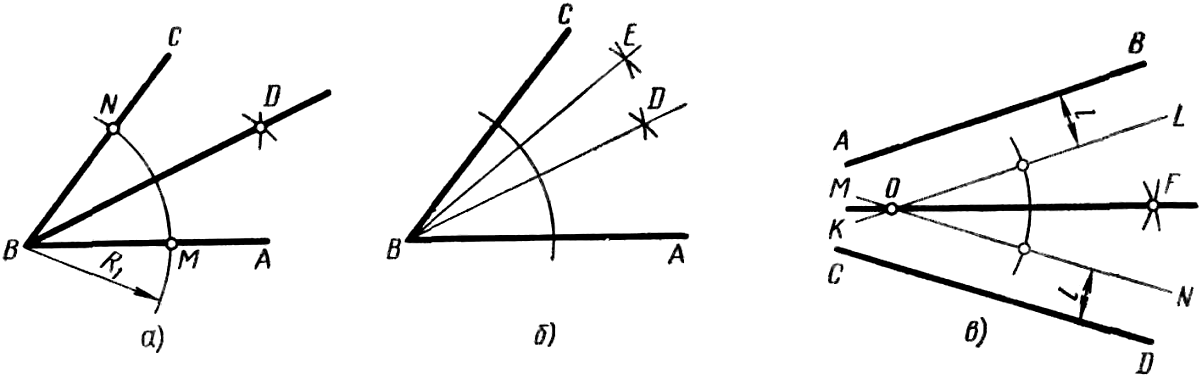
Рисунок 26
В том случае, когда угол задан сторонами, не пересекающимися в пределах чертежа, например AB и CD на рисунке 26, в, деление угла пополам выполняют так. На произвольном, но одинаковом расстоянии l от сторон угла проводят прямые KL || AB и MN || CD и продолжают их до пересечения в точке О. Полученный угол LON делят пополам прямой OF. Прямая OF разделит пополам также и заданный угол.
Деление прямого угла на три равные части (рисунок 27). Из вершины прямого угла – точки В проводят дугу произвольным радиусом R до пересечения ее с обеими сторонами угла в точках A и C. Тем же радиусом R из точек A и С проводят дуги до пересечения с дугой AC в точках М и N. Прямые, проведенные через вершину угла В и точки М и N, разделят прямой угол на три равные части.

Рисунок 27
ОБЩИЕ ПОЛОЖЕНИЯ
Очертания многих предметов представляют собой сочетание ряда линий, в большинстве своем плавно переходящих одна в другую. Примером плавных переходов могут служить контуры различных видов художественных изделий, посуды, рисунки орнаментов и т.п.
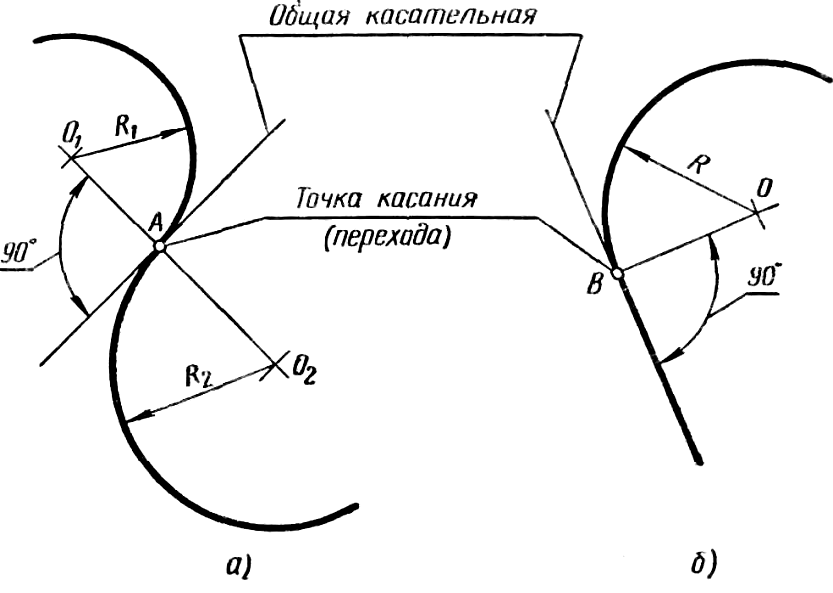
Плавный переход одной линии в другую называют касанием линий, а точку, в которой происходит касание, - точкой касания или перехода (рисунок 41). Например, две дуги радиусами R1 и R2, касающимися между собой (рисунок 41 а), имеют общую точку касания A, лежащую на линии, соединяющей центры этих дуг – точки O1 и O2. На рисунке 41, б изображена прямая, касающаяся дуги радиуса R и имеющая с ней общую точку касания B, расположенную на перпендикуляре, опущенном из центра дуги – точки О на прямую. Через любую точку касания можно провести общую касательную, которая будет перпендикулярна к радиусам дуг, проведенным в точку касания.
а б
Рисунок 41
Плавный переход одной линии в другую при помощи промежуточной линии называют сопряжением. На рисунке 42 такой промежуточной линией является дуга AB радиусом Rc, с помощью которой осуществлен плавный переход (сопряжение) от прямой к дуге окружности радиусом R.
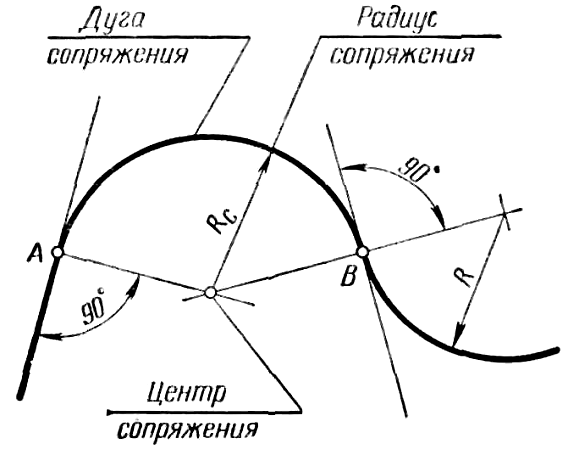
Рисунок 42
Чаще всего промежуточной линией является дуга окружности, называемая дугой сопряжения, или сопрягающей дугой. Радиус сопрягающей дуги носит название радиуса сопряжения, а центр дуги – центра сопряжения. Дуга сопряжения касается одновременно двух сопрягаемых линий. При сопряжении всегда имеются две точки перехода (на рисунке 42 точки А и B), и через каждую из них можно провести по одной общей касательной.
Таким образом, построение сопряжений основано на свойствах касательной к дуге окружности и касания двух дуг окружностей.
Касание окружностей
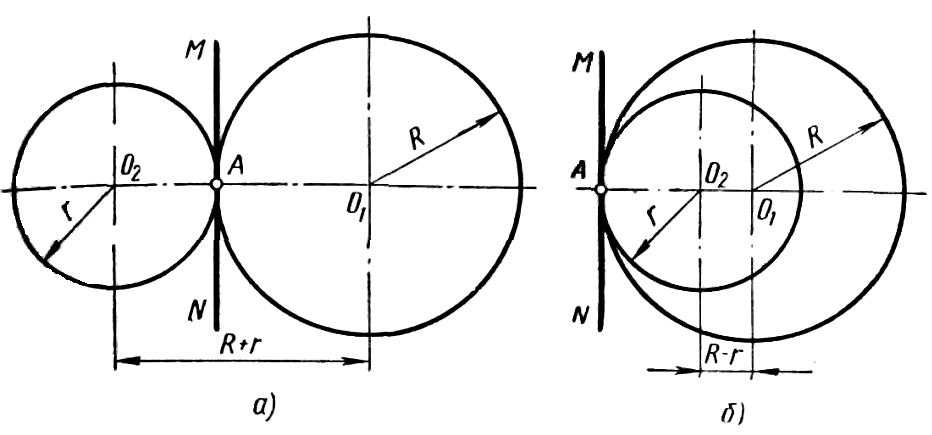
Различают два вида касания окружностей – внешнее и внутреннее. При внешнем касании окружностей радиусами R и r (рисунок 45, а) центры окружностей O1 и O2 располагаются по разные стороны от общей касательной MN, проведенной через точку касания A, а расстояние между ними равно сумме радиусов R + r. Точка касания A лежит на прямой, соединяющей центры касающихся окружностей.
а б
Рисунок 45
Внутреннее касание окружностей (рисунок 45, б) характеризуется тем, что центры касающихся окружностей O1 и O2 располагаются по одну сторону от общей касательной MN, проведенной через точку касания А, а расстояние между центрами касающихся окружностей равно разности радиусов R - r. Точка касания A окружностей в этом случае расположена на продолжении прямой, соединяющей их центры.
Построение окружности радиусом r, касающейся окружности радиусом R в данной на ней точке А. На рисунке 46 показано построение внутреннего касания окружностей. Точку A и центр O1 заданной окружности соединяют прямой. Радиусом R – r из центра O1 проводят дугу до пересечения ее с прямой O1A в точке O2. Точка O2 является искомым центром окружности радиуса r.
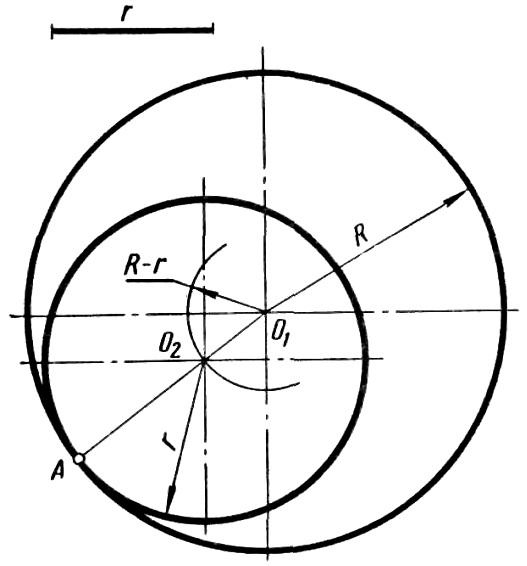
Рисунок 46
Архитектурные обломы
Многие здания снаружи и внутри имеют различные архитектурные украшения. Профиль архитектурных украшений складывается из элементов, называемых архитектурными обломами. Архитектурные обломы украшают не только здания. Их можно увидеть в контуре постаментов, декоративных ваз, мебели и т. п.
По форме архитектурные обломы могут быть прямолинейные (рису-нок 55) и криволинейные (рисунки 56, 57). Криволинейные обломы, такие как полувал, шейка, прямой и обратный четвертной вал, прямая и обратная выкружка (рисунок 56), очерчены при помощи одной дуги, и способ их построения понятен из чертежа. Более сложные криволинейные обломы состоят из двух дуг. К ним относятся: гусёк прямой и обратный, каблучок прямой и обратный, скоция, сложный торус (рисунок 57).
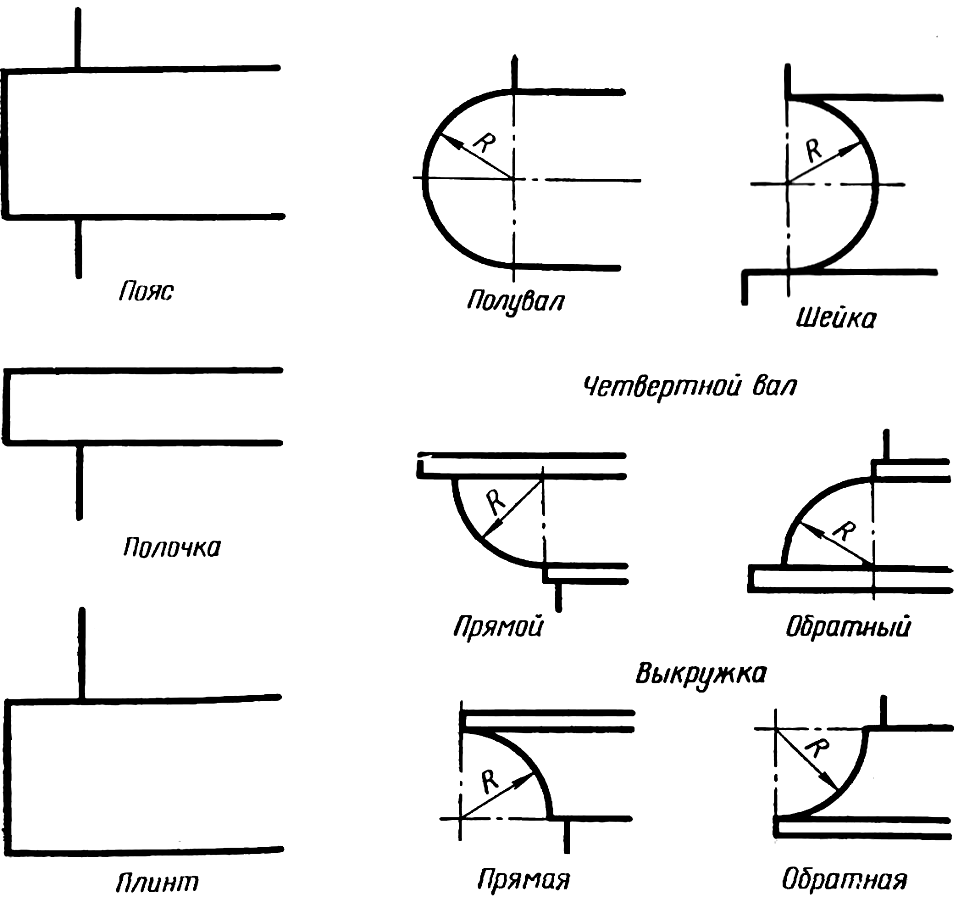
Рисунок 55 Рисунок 56
В построении гуська и каблучка много общего. Для построения, например, прямого гуська (рисунок 57, а) заданные точки А и В соединяют прямой линией. Отрезок AB делят пополам в точке С. Радиусом R = AC =CB из точек А, С и В проводят дуги до взаимного пересечения в точках O1 и O2 , и из них тем же радиусом R описывают две дуги, являющиеся профилем прямого гуська. Вычерчивание обратного гуська или одного из видов каблучка аналогично вычерчиванию прямого гуська, при этом меняется только положение центров O1 и O2 (рисунок 57, б, в, г). Сложный торус строят по заданному радиусу R (рисунок 57, д). Проводят прямую и на ней отмечают два центра – O1 и O2 на расстоянии 2R. Из центра O1 описывают четверть окружности радиусом R, а из центра O2 – радиусом 3R.
Для построения скоции также задают радиус R (рисунок 57, е) и строят шесть квадратов со сторонами, равными заданному радиусу. Наметив точки O1 и O2, описывают две дуги радиусами R и 2R.
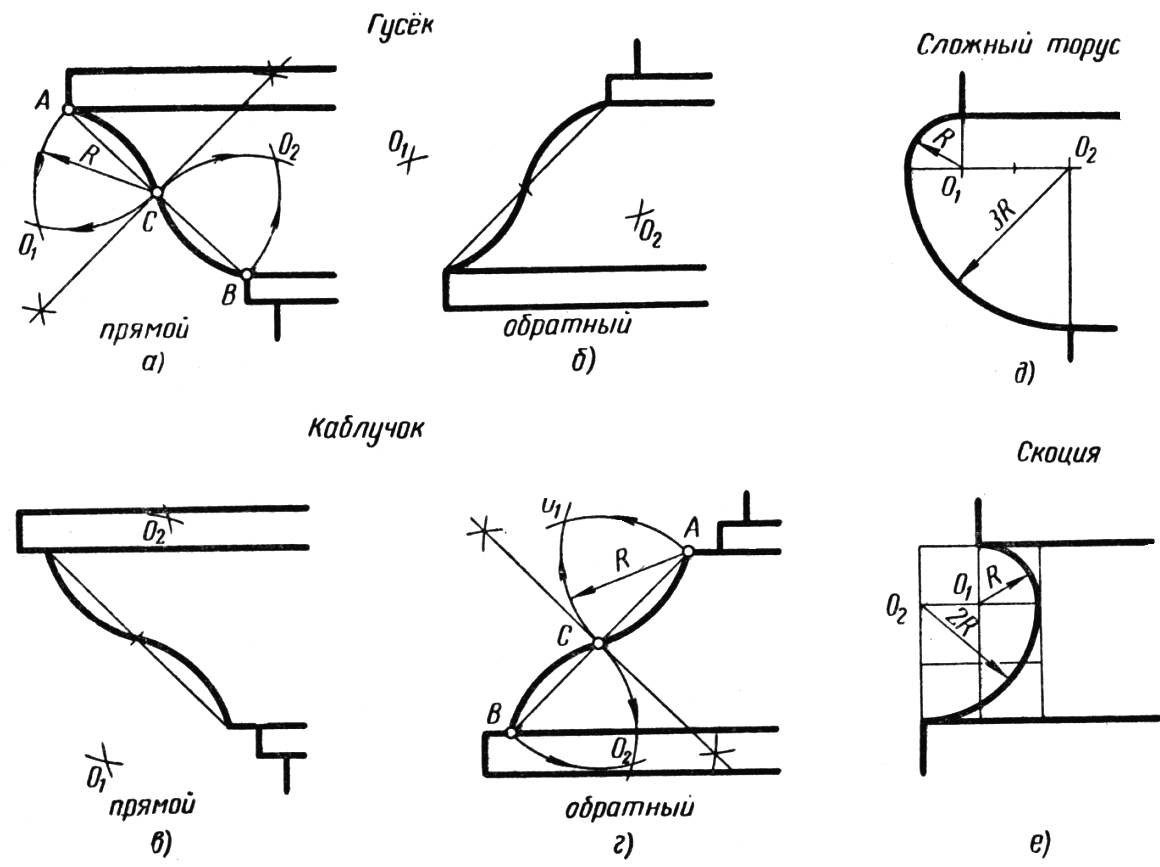
Рисунок 57
ПЛОСКИЕ КРИВЫЕ
Кривые, у которых все точки расположены в одной плоскости, называют плоскими. Часть плоских кривых, состоящих из дуг окружностей, образует группу циркульных кривых. Дуги циркульных кривых касаются друг друга, поэтому построение их основано на правилах сопряжения и выполняется при помощи циркуля.
Другая часть плоских кривых, которые нельзя построить с помощью циркуля, относится к группе лекальных кривых. Лекальные кривые строят по точкам, зная закон их образования, а обводят по лекалу.
ЦИРКУЛЬНЫЕ КРИВЫЕ
Завитки
Спиральная кривая, вычерченная циркулем путем сопряжения дуг окружностей различных радиусов, называется завитком. На рисунке 58, а показано построение двуцентрового завитка. Он состоит из ряда полуокружностей, описанных попеременно из заданных центров O1 и O2. Точки касания проводимых дуг расположены на прямой, соединяющей эти центры. Первую полуокружность описывают радиусом R, равным расстоянию между центрами O1 и O2. Радиус каждой последующей полуокружности увеличивают на величину первоначального радиуса R. Таким образом, вторую полуокружность описывают радиусом 2R, третью - радиусом 3R и т. д.
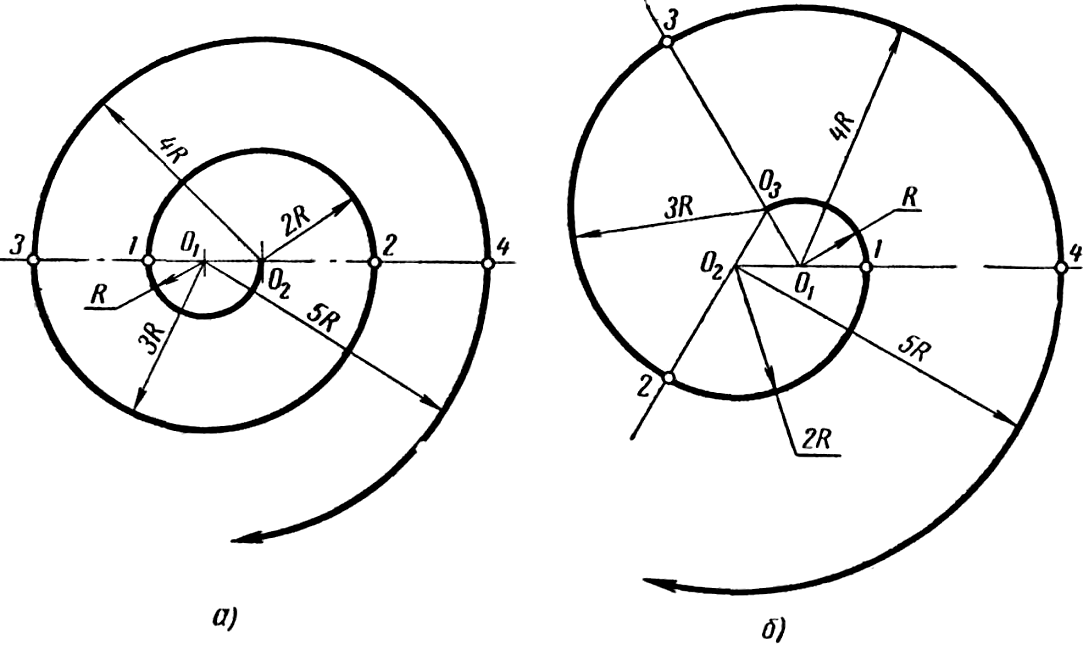
а б
Рисунок 58
Построение трехцентрового завитка по заданным центрам O1, O2 и O3, расположенных в вершинах равностороннего треугольника, приведено на рисунке 58, б. Через каждую пару центров проводят прямую линию. Из центра O1 описывают дугу радиусом R = O1O3 в пределах между точками O3 и 1. Следующую дугу радиусом 2R проводят из центра O2 до точки 2. Затем описывают дугу радиусом 3R из центра O3. Дуга, проведенная снова из центра O1, имеет радиус 4R и т. д.
Завитки четырехцентровые, пятицентровые и т. д. строят таким же образом.
Коробовые кривые
Коробовой кривой называется односторонне выпуклая циркульная кривая (замкнутая или незамкнутая), образуемая сопряжением дуг: окружностей. Существует несколько разновидностей коробовых кривых.
Овал – замкнутая коробовая кривая, имеющая две оси симметрии. Элементами, определяющими размер овала, являются его длина и ширина, измеряемые по осям симметрии.
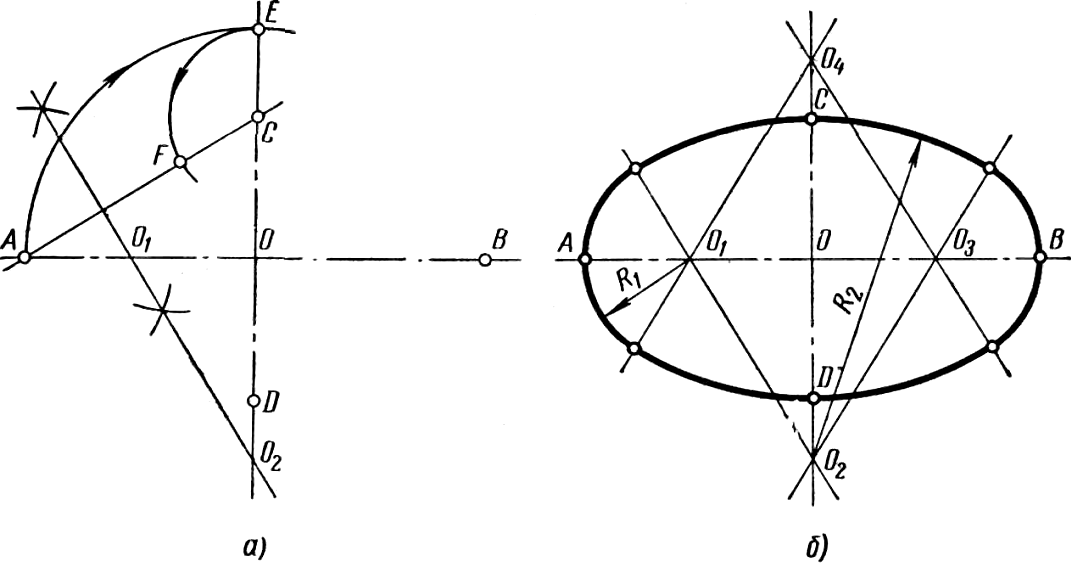
Построение овала по его длине AB и ширине CD показано на рисун-ке 59. Вначале проводят две взаимно перпендикулярные прямые, пересекающиеся в точке О (рисунок 59, а). На горизонтальной прямой в обе стороны от точки О откладывают отрезок 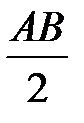 , а на вертикальной –
, а на вертикальной – 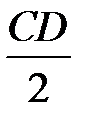 . Точки A и С соединяют прямой линией, и из точки О описывают дугу радиусом OA до пересечения ее с прямой CD в точке E. На прямой AC откладывают отрезок CF=CE и получают точку F. Через середину отрезка AF проводят перпендикуляр и на пересечении его с прямыми AB и CD получают точки O1 и O2. На прямых AB и CD строят точки O3 и O4, симметричные точкам O1 и O2 относительно центра О (рисунок 59 б). Точки O1, O2,O3, O4 являются центрами сопрягаемых дуг, определяющих контур овала, а точки касания дуг располагаются на прямых O1O2, O3O2, O1O4 и O3O4. Из центров O1 и O3 описывают дуги радиусом R1 = O1A, а из центров O2 и O4 – дуги радиусом R2 = O2C и получают контур овала.
. Точки A и С соединяют прямой линией, и из точки О описывают дугу радиусом OA до пересечения ее с прямой CD в точке E. На прямой AC откладывают отрезок CF=CE и получают точку F. Через середину отрезка AF проводят перпендикуляр и на пересечении его с прямыми AB и CD получают точки O1 и O2. На прямых AB и CD строят точки O3 и O4, симметричные точкам O1 и O2 относительно центра О (рисунок 59 б). Точки O1, O2,O3, O4 являются центрами сопрягаемых дуг, определяющих контур овала, а точки касания дуг располагаются на прямых O1O2, O3O2, O1O4 и O3O4. Из центров O1 и O3 описывают дуги радиусом R1 = O1A, а из центров O2 и O4 – дуги радиусом R2 = O2C и получают контур овала.
а б
Рисунок 59
Овоид – замкнутая коробовая кривая, имеющая одну ось симметрии. Построение овоида по его ширине – отрезку AB приведено на рисунке 60, а. Через середину отрезка AB – точку O1 проводят прямую, перпендикулярную к нему. Из точки O1 описывают окружность радиусом 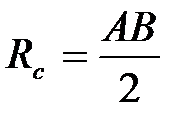 и на пересечении ее с перпендикуляром получают точку O2. Далее проводят прямые AO2 и BO2 и продолжают их за точку O2. Из точек A и В радиусом R2 = AB описывают две дуги до пересечения их в точках C и D с проведенными прямыми. Последнюю дугу радиусом R3 = O2C описывают из точки O2.
и на пересечении ее с перпендикуляром получают точку O2. Далее проводят прямые AO2 и BO2 и продолжают их за точку O2. Из точек A и В радиусом R2 = AB описывают две дуги до пересечения их в точках C и D с проведенными прямыми. Последнюю дугу радиусом R3 = O2C описывают из точки O2.
Если точку O2 расположить ближе к точке O1 или дальше от нее, то овоид получится соответственно более тупым или более острым. Для построения тупого овоида задают его ширину AB и расстояние между центрами O1O2 (рисунок 60 б). Порядок построения остается прежним.
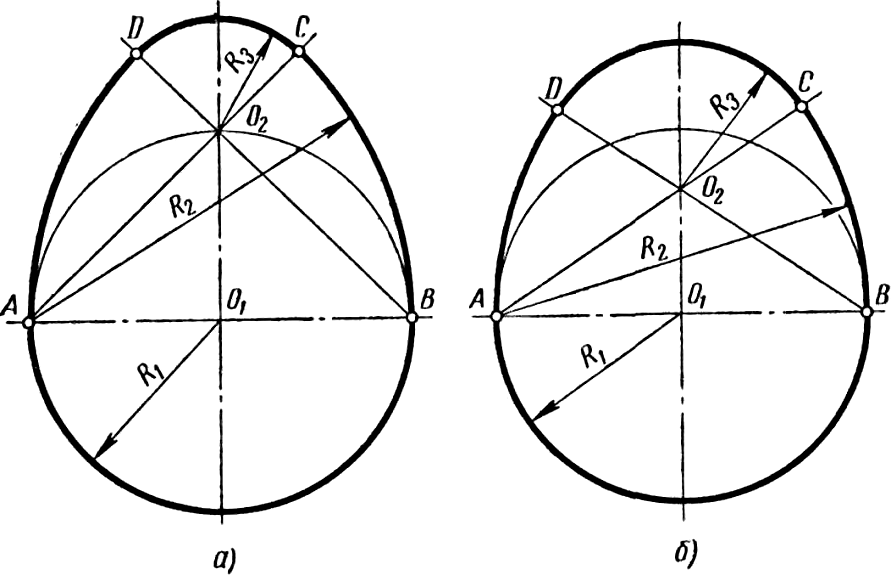
а б
Рисунок 60
Коробовые кривые сводов относятся к незамкнутым коробовым кривым. Они находят применение при строительстве сводов и арок мостов, входов в здания, различных перекрытий, например метро и т. п. Ниже разобрано построение коробовых кривых пологого, крутого и ползучего сводов.
Построение коробовой кривой пологого свода по его ширинеАВи высотеОС (рисунок 61). На горизонтальной прямой откладывают ширину свода – отрезок AB и через его середину точку О проводят прямую, перпендикулярную к нему. На этой прямой от точки О откладывают высоту свода – отрезок OC. Из точки О радиусом OA описывают дугу AE и на ней отмечают точку D с помощью того же радиуса OA, но с центром в точке А. Точку D соединяют прямыми с точками А, Е и О. Затем через точку С проводят прямую CF || DE до пересечения ее с прямой AD в точке F. Через точку F проводят прямую FO2 || DO до пересечения ее с отрезком AB в точке O1, а с прямой OC в точке O2. Точку O3 получают при помощи дуги радиусом OO1. Полученные точки O1, O2 и O
