Выполнение графической работы: Лекальные кривые

Все множество плоских кривых можно разделить на циркульные и лекальные. Циркульной называют кривую, которую можно построить с помощью циркуля. К ним относятся окружность, овал и т.д.

Лекальной называют плавную кривую линию, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.

Лекальные кривые можно разделить на закономерные и незакономерные.

Закономерными называют кривые, которые можно задать алгебраическим выражением. Незакономерные кривые нельзя задать алгебраическим выражением.

Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.

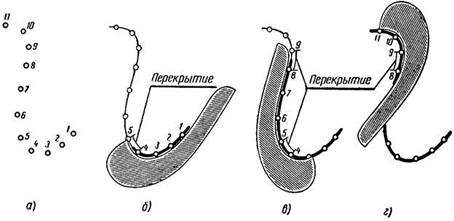
Рассмотрим построение лекальных кривых на примере Эллипса и Спирали Архимеда.

Задание:Выполнить чертеж лекальных кривых (эллипс, спираль Архимеда) на формате А4.Проставить размеры. Размеры даны в задачах (см. ниже). Название работы: Лекальные кривые.

Построение лекальной кривой – эллипса

Эллипс– это замкнутая кривая. Его большая и малая оси есть оси симметрии эллипса. Точки F1 и F2 - это фокусы эллипса. Сумма расстояний от любой точки эллипса (от М, от N, ...) до фокусов F1 и F2 есть величина постоянная. Она равна большой оси АВ. Например, F1M + F2M. = AB; F1N + F2>N=AB (рис. 17). Пример построения эллипса приведен на рис.2.

.

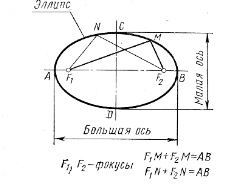
Рис. 1. Лекальная кривая – эллипс

1. Даны большая ось АВ и малая ось CD эллипса

2. Проводим из центра О окружность радиуса ОА и окружность радиуса ОС.

3. Делим большую окружность на 12 равных частей. Точки деления 1, 2, 3, 12 окружности соединяем с центром О. Прямые 1-7, 2-8 ... 6-12 делят малую окружность тоже на 12 равных частей.4. Из точек деления большой окружности проводим прямые параллельные CD. Из точек деления малой окружности проводим прямые, параллельные АВ. Точки пересечения вертикальных и горизонтальных прямых – это искомые точки эллипса. 5. Соединяем точки плавной кривой с помощью лекал (рис.2).

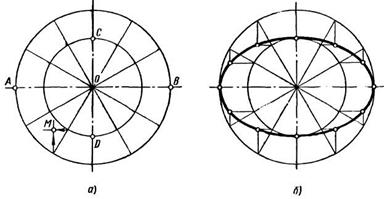
Рис. 2. Построение лекальной кривой – эллипса

Для выполнения данной задачи взять исходные данные: АB=70, СD=40, окружность разделить на 24 части.

Построение спирали Архимеда

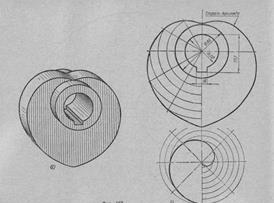
На рисунке дано изображение распределительного кулачка. Очертания его боковых сторон выполняют по спирали Архимеда.

Спиралью Архимеда называется плоская кривая, полученная как след точки, движущейся равномерно поступательно от неподвижной точки О по выходящему из нее и равномерно вращающемуся вокруг точки О лучу (радиусу). Точка О называется полюсом спирали; отрезок ОА называется шагом t спирали; отрезок KL – нормалью спирали, а прямая MN, перпендикулярная к нормали, называется касательной.

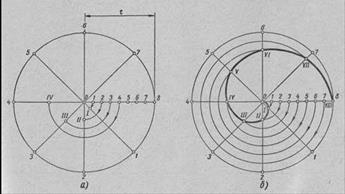Заданный шаг t спирали Архимеда делят на несколько, например, на восемь, равных частей. Из конца О отрезка / проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.

На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т.д.

После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую – спираль Архимеда.

Для выполнения задания на формате А4 взять следующие значения: R=t=55, окружность разделить на 12 частей.

Практическая № 11