Электрические станции, сети и системы

УТВЕРЖДАЮ

Зам.директора по УР

_________Н.В. Полубенцева

___________20____год

УЧЕБНОЕ ПОСОБИЕ

ДИСЦИПЛИНЫ ОП.01 ИНЖЕНЕРНАЯ ГРАФИКА

программы подготовки специалистов среднего звена

По специальности

Электрические станции, сети и системы

Иркутск, 2015

РАССМОТРЕНА Цикловой комиссией Информационных технологий председатель _____________ Н.А. Витязева _____________20___ год

ПРИНЯТА Методическим советом колледжа протокол №___ от___________ 20___года

Разработчик: Яровая Е.С. – преподаватель ГБПОУ «ИЭК»

Введение

Важное место в подготовке обучающихся колледжа занимает учебная дисциплина Инженерная графика. Умение читать и выполнять чертежи - необходимое условие успешной работы на производстве. Поэтому целью изучения дисциплины Инженерная графика является приобретение прочных теоретических знаний и практических навыков.

На реализацию этой цели направлено данное учебное пособие. Оно отражает требования, содержащиеся в двух первых разделах рабочей программы учебной дисциплины.

В данном пособии содержатся практические работы, включающие теоретический материал, графические задания, задачи. Также в пособии представлены задания для самостоятельной работы студентов.

Пособие предназначено для студентов очной и заочной формы обучения и призвано систематизировать знания обучающихся, повысить качество освоения дисциплины.

Практическое занятие №1

Введение в Инженерную графику

Графика — это способ отображения окружающей нас действительности на плоскости. Графика вмещает в себя множество способов изображения. Рассмотрим два из них: рисунок и чертеж

Рисунок — это графическое изображение, выполненное от руки на глаз, которое дает нам представление только о внешнем виде предмета и не дает представления о внутреннем его устройстве и размерах.

Чертеж — это графическое изображение, выполненное при помощи специальных чертежных инструментов и принадлежностей по особым правилам построения изображений, которое дает нам полное представление о внешнем и внутреннем устройстве предмета № о его размерах.

Практическое занятие №2

Выполнение графической работы: Типы линий

Все чертежи выполняются линиями по ГОСТ 2.303-68, который устанавливает основные назначения линий и их начертания (таблица). На одном чертеже толщина однотипных линий должна быть одинаковой. Толщина всех типов линий зависит от толщины сплошной толстой, основной линии, которая выбирается в пределах от 0,5 до 1,4 мм в зависимости от формата чертежа, величины и сложности изображения, а также от назначения чертежа.

Проводя штриховую или штрихпунктирную линию, необходимо следить, чтобы всё штрихи и промежутки между ними были равны между собой по длине.

,

Задание:

Выполнить на листе формата А4 данное задание, соблюдая типы линий. Толщину и другие размеры линий выполнять в соответствии с ГОСТ 2.303-68. Размеры не проставлять.

Практическое занятие №3

Масштабы

Выполняя чертеж, не всегда можно изобразить, предмет в его действительных размерах. Например, нельзя вычертить в натуральную величину здание или станок, их изображают в уменьшенном виде. А мелкие предметы, такие, как детали часового механизма наручных часов, необходимо увеличить, так как их не только невозможно начертить в натуральную величину и проставить размеры, но и нельзя прочитать такой чертеж. Поэтому при выполнении чертежей пользуются масштабами.

Масштаб представляет собой отношение линейных размеров изображенного на чертеже предмета к их натуральной величине. Для изображения предмета в увеличенном виде применяется масштаб увеличения, а в уменьшенном виде – масштаб уменьшения. Для изображения предмета в натуральную величину используют его действительные размеры. Масштабы согласно ГОСТ 2.302-68 приведены в таблице. Предпочтение следует отдавать масштабу 1:1, так как по такому изображению легче судить о форме и действительных размерах предмета. В каком бы масштабе не выполнялось изображение, на чертеже проставляются действительные размеры детали. На чертеже обязательно должен указываться масштаб. Если он проставляется в специальной графе основной надписи, то пишется так: 1:1; 2:1; 1:2 (в зависимости от того, в каком масштабе выполнено изображение). Если масштаб указывается на поле чертежа, то перед числами ставится буква М, что обозначает масштаб, например, М1:1; М2:1 или М1:2.

Масштабы
Уменьшения	1:2; 1:2,5; 1:4; 1:5; 1:10…….1:20; 1…..1000
В натуральную величину	1:1
Увеличения	2:1; 2,5:1; 4:1; 5:1; 10:1……..1000:1.

Практическое занятие №4

Практическое занятие №5

Практическое занятие №6

Самостоятельная работа №1

Практическое занятие №7

Задание выполняется в рабочей тетради.

Деление отрезка прямой на две и четыре равные части Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в. Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части. Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части.

Деление отрезка прямой на любое число равных частей. Пусть отрезок АВ требуется разделить на 9 равных частей. Для этого из любого конца отрезка (из точки А) проведем под острым углом к отрезку прямую линию, на которой от точки А измерительным циркулем откладываем 9-ть равных отрезков произвольной величины. Точку 9 соединяем с точкой В (концом данного отрезка) прямой. Из точек 1, 2, ... 8 проведем ряд прямых параллельных прямой 9А, которые пересекая отрезок АВ разделят его на 9 равных частей.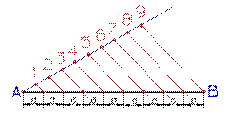

Практическое занятие №8

Практическое занятие № 9

Выполнение графической работы: Вычерчивание контура детали с применением сопряжения

Задание:Построить изображение плоского контура детали с выполнением сопряжений на формате А4 (формат располагается вертикально). Масштаб – 1:2. Исходные данные приведены ниже. Линии построения не стирать.

Цель работы: Изучение типов линий и приобретение навыков их выполнения (ГОСТ 2.303-68). Изучение построений сопряжений в очертаниях технических форм. Ознакомление с основными правилами нанесения размеров (ГОСТ 2.307-68). Изучение приемов написания букв и цифр чертежным шрифтом (ГОСТ 2.304-81). Применение масштаба.

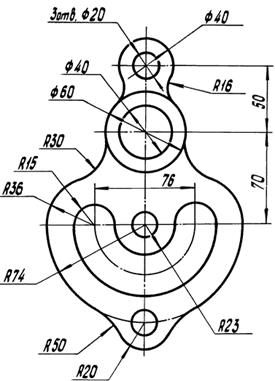Последовательность выполнения задания: 1. Подготовить формат А4. Нанести внутреннюю рамку и прямоугольник основной надписи. 2. По размерам, нанесенным на исходные данные, установить габариты изображения и спланировать габаритный прямоугольник на чертеже так, чтобы очерк детали расположился примерно в середине поля формата. 3. Выбрать базовые линии очерка детали и нанести их на чертеже. Вычертить в тонких линиях контур детали, проведя все вспомогательные построения для центров и точек сопряжения линий. 4. Нанести выносные и размерные линии (ГОСТ 2.307-68). Особое внимание следует обратить на расположение размерных чисел над размерными линиями. 5. Сделать обводку чертежа. 6. Заполнить основную надпись чертежным шрифтом.

Практическое занятие № 10

Практическая № 11

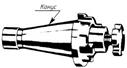
Конусности. ГОСТ 8593-81

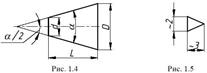
Конусность – это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 1.4).

C = (D – d) / L = 2 tg a / 2.

Для обозначения конусности на чертеже применяется знак (рис. 1.5) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, характеризующим конусность, острый угол знака должен быть направлен в сторону вершины конуса (рис. 1.6).

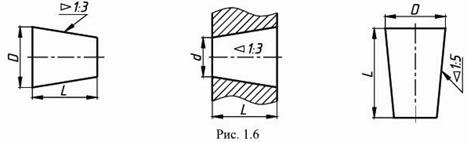
Если нужно построить конусность 1:n относительно заданной оси, то строим уклоны 1:2n с каждой стороны оси.

Задание: Построить в тетради уклон 1: 8 и конусность 1:7.

Самостоятельная работа № 2

Практическое занятие № 12

Практическое занятие № 13

Практическое занятие № 14

Образование чертежа точки в системе двух и трех плоскостей проекций

Данный метод позволяет определить место каждой точки изображения относительно других точек.

Точку (предмет) помещают в систему двух взаимоперпендикулярных плоскостей, которые используются в качестве плоскостей проекций.

П1 - горизонтальная плоскость проекций;

П2 - фронтальная плоскость проекций;

х - ось проекций

А1 - горизонтальная проекция точки А,

А2 - фронтальная проекция точки А.

Если даны проекции А1 и А2 некоторой точки А, то проведя перпендикуляры: через т.А1 к плоскости П1, а через т. А2 к П2, получим в пересечении этих прямых определенную точку А (рис.5).

Вращением вокруг оси ОX плоскость П1 совместим с плоскостью П2. При этом проекции А2 и А1 точки А расположатся на одном перпендикуляре к оси проекций - на линии связи.

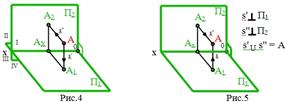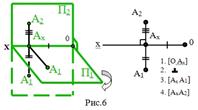В результате указанного совмещения плоскостей П2 и П1 получается чертеж, известный под названием эпюр Монжа или двухкартинный чертеж, включающий две взаимосвязанные проекции - “картины”.

Известно, что чертежи сложных конструкций содержат не две, а большее число изображений - проекций. Рассмотрим введение в систему П1, П2 еще одной плоскости проекций, перпендикулярной П1 и П2 (рис.7).

П3 - профильная плоскость проекций.

Опустим перпендикуляр на плоскость П3 из точки А и получим.

А3 - профильную проекцию точки А (рис.8).

Для получения трехкартинного чертежа точки надо повернуть плоскость П1 вокруг оси x и плоскость П3 вокруг оси z до совмещения их с плоскостью П2 (рис.9).

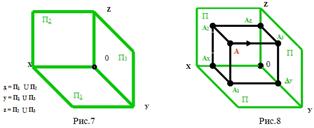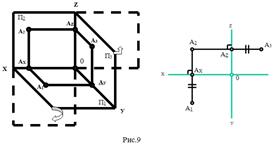Вывод: Каждая точка пространства характеризуется тремя координатами: А (х, у, z).

Задание: Построить в рабочей тетради комплексный чертеж точки А (17;13;25)

Практическое занятие № 15

Практическое занятие № 16

Заполнение сводных таблиц: Общее и частные положения плоскости в пространстве

I. Плоскость общего положения.Плоскость наклонная ко всем трем плоскостям проекций.

II. Плоскость частного положения. Плоскость перпендикулярная к одной или одновременно к двум плоскостям проекций. Плоскости частного положения делятся на три вида:

1) Проецирующие плоскости:

а)горизонтально-проецирующая плоскость, т.е. перпендикулярная к П1. И поэтому она проецируется на П1 в виде прямой линии.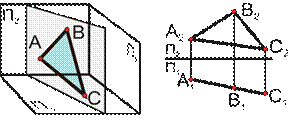
б)фронтально-проецирующая плоскость, т.е. перпендикулярная к П2. И поэтому она проецируется на П2 в виде прямой линии.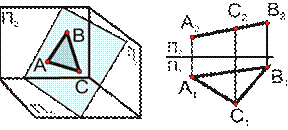
в) профильно-проецирующая плоскость, т.е. перпендикулярная к П3. И поэтому она проецируется на П3 в виде прямой линии.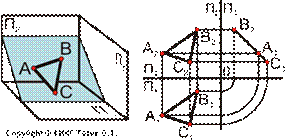

2) Плоскости уровня:

Плоскость уровня - плоскость перпендикулярна сразу к двум плоскостям проекций, следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций.

а) горизонтальная плоскость уровня - параллельная П1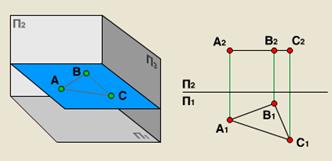
б) фронтальная плоскость уровня - параллельная П2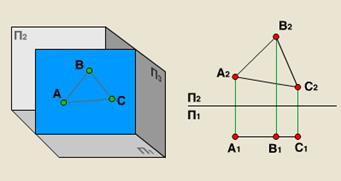
в) профильная плоскость уровня - параллельная П3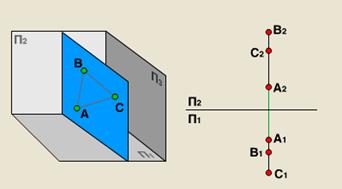

Практическое занятие № 17

Практическое занятие № 18

Выполнение графической работы: Способы преобразования ортогонального чертежа

Решение позиционных и метрических задач становится проще, если геометрические фигуры находятся в частном положении относительно плоскостей проекций. Для того, чтобы геометрические фигуры заняли частное положение, необходимо выполнить преобразование чертежа. Существует два основных способа преобразования ортогонального чертежа:

- способ введения дополнительных плоскостей проекций;

- способ вращения вокруг прямой.

Сущность первого способа заключается в том, что геометрический объект пространства вместе с системой координат не меняет своего положения в пространстве, а новая плоскость проекций П₃ П₁ (или П₃ П₂) занимает частное положение по отношению к заданному объекту.

Во втором случае плоскости проекций не меняют своего положения в пространстве, а геометрический объект путем поворота вокруг надлежаще выбранной оси занимает частное положение по отношению к плоскостям проекций.

Рассмотрим первый способ – метод замены плоскостей проекций. Суть способа состоит во введении новой дополнительной плоскости проекций П₃ перпендикулярной одной из исходных плоскостей (либо П₁ либо П₂). Заданные геометрические фигуры ортогонально проецируют на новую плоскость проекций.

Рассмотрим схему построения чертежа на примере проецирования точки А на дополнительную плоскость П₃ П₁ см. рис)

Прямую пересечения новой плоскости П₃ с исходной П₁ принимаем за новую ось проекции. Вращением на 90° вокруг новой оси П₁/П₃ совмещаем новую плоскость проекций П₃ с плоскостью П₁ на первом этапе. Затем на втором этапе совмещаем эти объединенные плоскости с плоскостью П₂ поворотом на 90° вокруг оси П₂/П₁ Можно сказать, что в этом случае плоскость чертежа совмещается с фронтальной плоскостью проекций П₂.

Алгоритм построения чертежа точки :

1. Проводим ось проекций П₁/П₃;

2. Строим новую линию проекционной связи из точки A₁ перпендикулярную оси П₁/П₃;

3. Откладываем от точки Пересечения новой линии проекционной связи с осью П₁/П₃ высоту точки A (аппликату Z), равную расстоянию от A₂ до старой оси П₁/П₂

Из рассмотренного промера можно вывести общие свойства чертежа с дополнительными плоскостями проекций:

1. Линии связи перпендикулярны осям проекций;

2. Расстояние от старой не общей проекции А₂ до старой оси равно расстоянию от новой оси до новой проекции А₃. [Легче данное правило запомнить с помощью следующей мнемонической формулировки: «Рукава рубашки должны быть равны»]. Рассмотрим аналогичную задачу проецирования точки А на новую дополнительную плоскость П₄ перпендикулярную П₂.

Для этого вводим новую ось проекций П₂/П₄. Из точки А₂ проводим новую линию проекционной связи, перпендикулярную оси П₂/П₄, на ней от точки пересечения линии проекционной связи с осью П₂/П₄ откладываем ординату точки A, равную расстоянию от A₁ до оси П₁/П₂. Для решения некоторых задач достаточно выполнить одну замену плоскостей проекций. Решение других задач могут потребовать выполнения двух замен и более. Мы можем вводить любое количество дополнительных плоскостей проекций. Причем они вводятся последовательно друг за другом для замены уже введенных дополнительных плоскостей проекций.

На рисунке ниже можно видеть, что вначале вводится дополнительная плоскость проекций П₃ П₁, а затем новая плоскость П₄ П₃.

Определить длину отрезка AВ и угол его наклона к плоскости проекций можно путем введения одной дополнительной плоскостей проекций, причем расположить ее так, чтобы она была параллельна исходному отрезку. При этом дополнительная плоскость П₃ может быть перпендикулярной либо к П₁ либо П₂. Это зависит от того, какой угол наклона мы должны определить.

Рассмотрим пример, когда необходимо определить длину отрезка АВ и его угол наклона к плоскости П₁ (угол a).

Алгоритм графических построений:

Вводим дополнительную плоскость П₃ || АВ и одновременно П₃ П₁ (для определения угла a). Для этого проводим ось проекций П₁/П₃ параллельно A₁B₁;

1. Проводим линии проекционной связи в системе плоскостей проекции П₁ - П₃ перпендикулярно оси П₁/П₃;
2. Откладываем на них от оси П₁/П₃ расстояния равные расстояниям от А₂ и B₂ до оси П₁/П₂;
3. Соединяем А₃ и B₃. Длина проекции А₃B₃ равна длине отрезка |АВ|. Угол a – угол наклона А₃B₃ к оси П₁/П₃ - равен углу наклона АВ к плоскости проекций П₁

Если нам требуется найти угол наклона отрезка AB к плоскости П₂ (угол b), то дополнительную плоскость проекций П₃ следует вводить параллельно A₂B и перпендикулярно П₂. Все построения аналогичны.

Практическое занятие № 19

Практическое занятие № 20

Вопросы:

Практическое занятие № 21

Проекции геометрических тел

Точки на поверхности тел

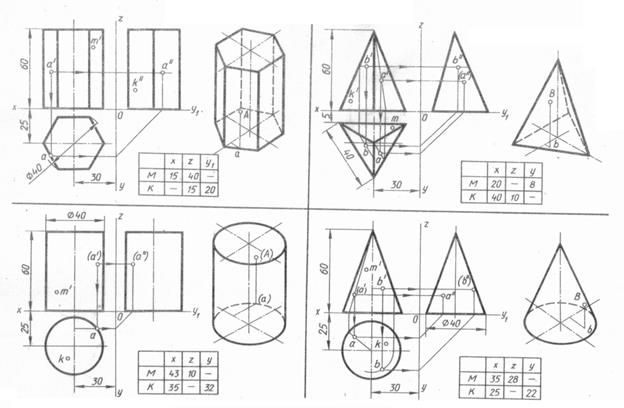
Задание:Перечертить геометрические тела и построить, принадлежащие их поверхностям точки А, В, М, К на ортогональном чертеже и в изометрии. Проекции точки А на призме и цилиндре и проекции точек А и В на пирамиде и конусе изображены построенными (для примера), точки М и К заданы одной проекцией. Необходимо найти положение точек М и К на оставшихся плоскостях проекций. На занятии выполняется только задание «Пирамида», далее необходимо завершить графическую работу в рамках Самостоятельной работы.

Задание выполняется на листе А3 в масштабе 1:2.

Практическое занятие № 22

Задание:

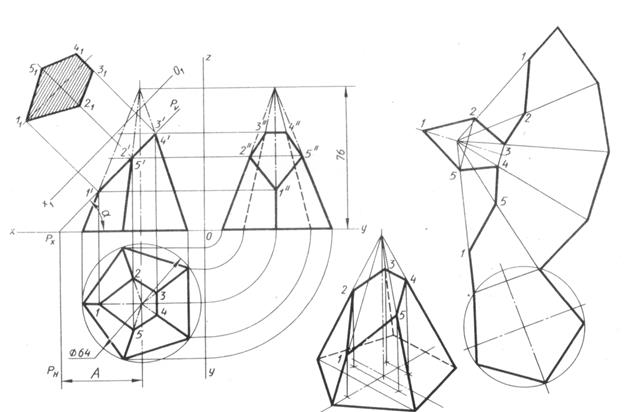
Построить три проекции пятиугольной пирамиды, усеченной плоскостью Р, натуральную величину сечения, развертку и изометрию.

Работа выполняется по вариантам на листах формата А3(три проекции + изометрия) и А4 (развертка)

№ варианта	Градус угла «альфа»	А

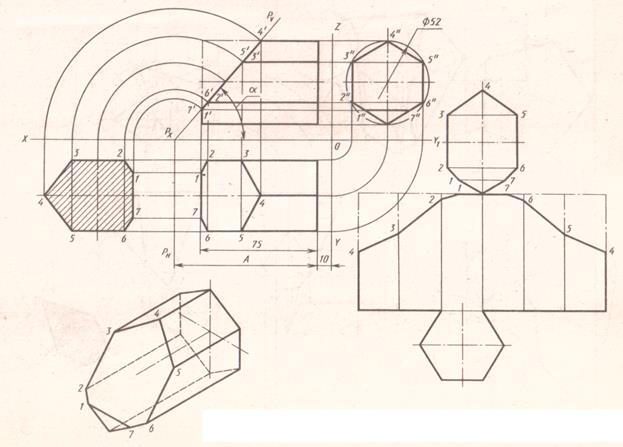
Построить три проекции шестиугольной призмы, усеченной плоскостью Р, натуральную величину сечения, развертку и изометрию.

Работа выполняется по вариантам на листах формата А3(три проекции + изометрия) и А4 (развертка)

№ варианта	Градус угла «альфа»	А

Самостоятельная работа № 3

Выполнение графической работы: «Проекции геометрических тел. Точки на поверхности тел» (цилиндр, конус, пирамида)

Задание: Продолжить выполнение графической работы (Практическое занятие №21) на формате А3.

Перечертить геометрические тела (пирамида, конус, цилиндр) и построить, принадлежащие их поверхностям точки А, В, М, К на ортогональном чертеже и в изометрии. Проекции точки А на призме и цилиндре и проекции точек А и В на пирамиде и конусе изображены построенными (для примера), точки М и К заданы одной проекцией. Необходимо найти положение точек М и К на оставшихся плоскостях проекций. Задание выполняется на листе А3 в масштабе 1:2.

Практическое занятие №23

УТВЕРЖДАЮ

Зам.директора по УР

_________Н.В. Полубенцева

___________20____год

УЧЕБНОЕ ПОСОБИЕ

ДИСЦИПЛИНЫ ОП.01 ИНЖЕНЕРНАЯ ГРАФИКА

программы подготовки специалистов среднего звена

По специальности

Электрические станции, сети и системы

Иркутск, 2015

РАССМОТРЕНА Цикловой комиссией Информационных технологий председатель _____________ Н.А. Витязева _____________20___ год

ПРИНЯТА Методическим советом колледжа протокол №___ от___________ 20___года

Разработчик: Яровая Е.С. – преподаватель ГБПОУ «ИЭК»

Введение

Важное место в подготовке обучающихся колледжа занимает учебная дисциплина Инженерная графика. Умение читать и выполнять чертежи - необходимое условие успешной работы на производстве. Поэтому целью изучения дисциплины Инженерная графика является приобретение прочных теоретических знаний и практических навыков.

На реализацию этой цели направлено данное учебное пособие. Оно отражает требования, содержащиеся в двух первых разделах рабочей программы учебной дисциплины.

В данном пособии содержатся практические работы, включающие теоретический материал, графические задания, задачи. Также в пособии представлены задания для самостоятельной работы студентов.

Пособие предназначено для студентов очной и заочной формы обучения и призвано систематизировать знания обучающихся, повысить качество освоения дисциплины.

Практическое занятие №1