Применение разверток в технике.

Развертки поверхностей широко применяются в технике. Многие технические конструкции выполняются из листового материала. Заготовки этих конструкций представляют собой их развёртки. Они применяются в автомобильной, авиа- и судостроительной промышленности, химической, легкой промышленности и т.д., при изготовлении воздуховодов для промышленной вентиляции в виде переходов с круглого сечения одного диаметра на круглое сечение другого диаметра, с круглого на прямоугольное сечение, бункеров и т.д.

Вопросы для самопроверки.

1.Какие задачи называются метрическими?

2.В чем состоит способ прямоугольного треугольника для определения натуральной величины отрезка прямой?

3.Когда прямой угол проецируется без искажения:

а) на горизонтальную плоскость проекций;

б) на фронтальную плоскость проекций?

4.Сформулируйте условие перпендикулярности прямой линии и плоскости на чертеже Монжа.

5.В чем сущность построения развертки многогранников?

6.Как строится приближенная развертка наклонного конуса?

7.В чем сущность построения условной развертки неразвертывающейся поверхности вращения (на примере тора или сферы)?

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ.

9.1. Основные понятия и определения.

Для получения наглядного изображения фигуры или объекта в системе координат OXYZ служат аксонометрические проекции. Возьмём в пространстве некоторую прямоугольную систему осей координат OXYZ и произвольную точку А. Опустим из точки А перпендикуляр на плоскость XOY, получим горизонтальную проекцию A₁ точки А. Аналогично можно найти проекции точки А на плоскости XOZ и YOZ. Далее возьмём в пространстве некоторую плоскость П’ и направление`S и будем проецировать точку А вместе с системой прямоугольных координат, к которой она отнесена в пространстве, параллельно некоторому направлению`S на плоскость П’.

При этом точка А спроецируется в А’,А₁ – в А’₁, ось ОХ – в ось О’X’ и т.д. (рис. 84). Натуральным масштабам е_x, е_у, е_z, которые берутся равными, будут соответствовать отрезки е’_х, е’_у, е’_z, которые, вообще говоря, не равны между собой.

Рис. 84

Так как при параллельном проецировании сохраняется параллельность прямых, то получим, что A’A’₁ || О’Z’, А₁’А’₁₂ || О’Y’ и т.д. Проекции всех геометрических элементов на плоскость П’ называются аксонометрическими. Например, А’ – аксонометрическая проекция точки А, A₁’ – аксонометрическая проекция точки А₁, которая в свою очередь, является горизонтальной проекцией точки А на плоскость XOY. Поэтому A₁’ называется вторичной проекцией точки А.

О’X’Y’Z’ – аксонометрическая система координат, проекции единичных отрезков на оси О’Х’, О’У’, O’Z’, обозначенные через е’_х, е’_у, е’_z – аксонометрические масштабы и т.д.

Отношение аксонометрических масштабов к натуральным называется показателями искажения.

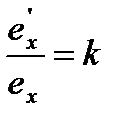– показатель искажения по оси OX;

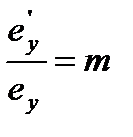– показатель искажения по оси OY;

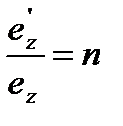– показатель искажения по оси OZ.

В зависимости от показателей искажения различают три вида аксонометрических проекций: изометрическая, если k = m = n, диметрическая, если два показателя искажения равны, например, k = m ¹ n; триметрическая проекции, если k ¹ m ¹ n.

В зависимости от направления проецирования рассматривают два вида аксонометрических проекций: если направление проецирования`S перпендикулярно плоскости П’, то такая проекция называется прямоугольной, если 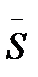не перпендикулярно П’, то аксонометрическая проекция называется косоугольной.