Взаимное пересечение плоскости и поверхности (3 группа позиционных задач)

В сечении поверхности плоскостью получается плоская фигура, которую строят по точкам. При этом начинают построение с опорных точек - точек, лежащих на линиях контура, ребрах и линиях основания поверхности.

Если проекция линии пересечения этими точками не определяется полностью, то строят дополнительные промежуточные точки. Чертеж всегда можно преобразовать заменой плоскостей проекций так, чтобы секущая плоскость стала проецирующей.

Поэтому начнем рассматривать случаи пересечения поверхности и плоскости частного положения.

Вариант А-1. Плоскость и поверхность являются проецирующими к разным плоскостям проекций(рис. 6.9).

S1^P2 ; S2^P1 - призма S1 Ç S2 = m ; S1^P2 Þ m2 = S12 1 = l Ç S1 2 = k Ç S1 3 = p Ç S1 m2 = (122232) m1= (112131) = S21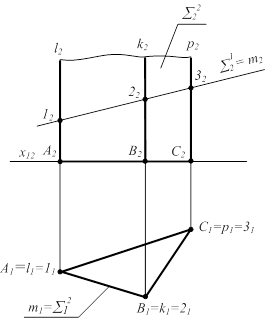

Рисунок 6.9

Вариант А-2. Плоскость и поверхность являются проецирующими относительно одной плоскости проекций(рис. 6.10).

S1 - плоскость S2 - поверхность S1 Ç S2 = m ­S1^ P1 S2^ P1 - цилиндр S1 Ç S2 ={a,b}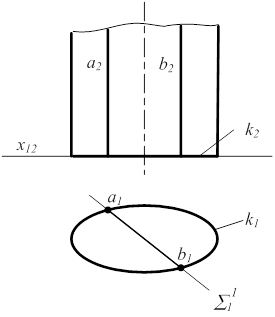

Рисунок 6.10

Вариант В-1. Плоскость проецирующая пересекается с поверхностью общего положения(рис. 6.11).

S1^P2 ; S2 - пирамида S1Ç S2 = m 1 = S1 Ç (SA) 2 = S1 Ç (SB) 3 = S1 Ç (SC) m2 = (122232) m1 = (112131) - по принадлежности m поверхности S2 - пирамиды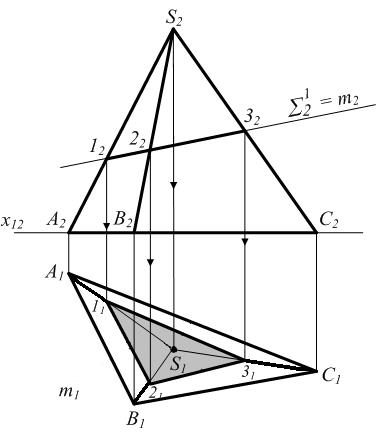

Рисунок 6.11

Вариант В-2. Плоскость общего положения пересекается с проецирующей поверхностью(рис. 6.12).

S1 (f Ç h) – общего положения. S2^ P1 - призма S1 Ç S2 = m (1;2;3) 1 = l Ç S1 ; l1 = 11 2 = k Ç S1 ; k1 = 21 3 = p Ç S1 ; p1 = 31 m1 = (112131). Точки сечения 1,2,3 находятся по принадлежности плоскости S(fÇh). 11 Ì h′1 ; h′ Ì S h′1 || h1 ; 12 Ì h′2 Аналогично определяются фронтальные проекции т.2 и 3 m2 = (12;22;32), m = [1;2;3]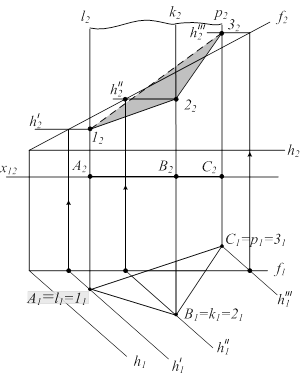

Рисунок 6.12

Вариант С. Плоскость и поверхность общего положения(рис. 6.13).

Целесообразно заменой плоскостей проекций привести к варианту В-1

S1 (f Ç h); S2 - пирамида; S1 Ç S2 = m(1;2;3) P2 ®P4^S1Þx14^h1ÌS1 1 = S1Ç (SA) 2 = S1 Ç (SB) 3 = S1 Ç (SC) m4 = [14,24,34] mÌS2; Þ m1(11,21,31) и m2(12,22,32)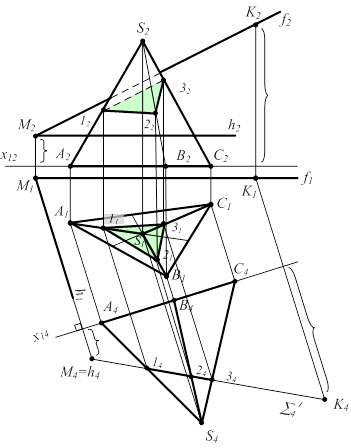

Рисунок 6.13

Рассмотрим решение этой же задачи по общему алгоритму. Вводим вспомогательные плоскости через ребра пирамиды (рис. 6.14).

1) Г1ÉSA ;G 1^P2 2) G1ÇS1 = a ; (G12 = a2) a2Çf2 ; a2Çh2 3) a Ç (SA) = 1 (a1ÇS1A1) Вводим пл. Г2 1) Г2 ÉSB; Г2^P2 2) Г2 Ç S1 = b ; (G22 = b2) b2Çf2 ; b2Çh2 3) b Ç (SB) =2 ; (b1ÇS1B1) Вводим пл. Г3 через ребро SC и повторяем алгоритм, находим т.3.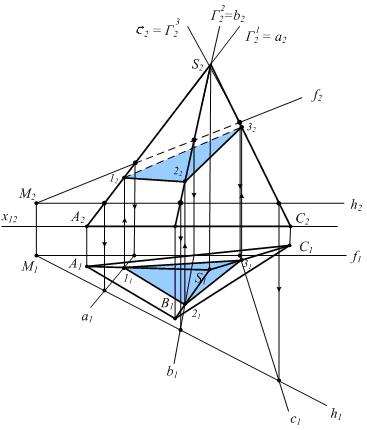

Рисунок 6.14

При пересечении криволинейных поверхностей или поверхностей вращения плоскостью вспомогательные плоскости вводятся через образующие поверхностей или перпендикулярно оси вращения. Найденные точки соединяются по лекалу.

В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии:

- окружность, если секущая плоскость перпендикулярна оси вращения цилиндрической поверхности;

- эллипс, если секущая плоскость не перпендикулярна и не параллельна оси вращения;

- две образующие прямые, если секущая плоскость параллельна оси вращения.

В сечении конической поверхности вращения плоскостью могут быть получены следующие линии:

- окружность, если секущая плоскость перпендикулярна оси вращения;

- эллипс, если секущая плоскость пересекает все образующие;

- парабола, если секущая плоскость параллельна только одной образующей;

- гипербола, если секущая плоскость параллельна двум образующим;

- две образующие прямые, если секущая плоскость проходит через вершину.

В сечении сферы плоскостью всегда получается окружность.