Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
3) Свойства и признаки равнобедренного треугольника
Равнобедренный треугольник — треугольник у которого равны две стороны. 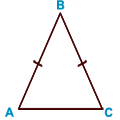 Например : AB = BC — боковые стороны; AC — основание равнобедренного треугольника. Например : AB = BC — боковые стороны; AC — основание равнобедренного треугольника. 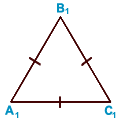 Равносторонний треугольник — треугольник у которого все стороны равны. Например : A 1B 1 = B 1C 1 = A 1C 1 — стороны треугольника. Всякий равносторонний треугольник является равнобедренным, но не всякий равнобедренный — равносторонним. Равносторонний треугольник — треугольник у которого все стороны равны. Например : A 1B 1 = B 1C 1 = A 1C 1 — стороны треугольника. Всякий равносторонний треугольник является равнобедренным, но не всякий равнобедренный — равносторонним. | ||
Свойства равнобедренного треугольника: • в равнобедренном треугольнике углы при основании равны; 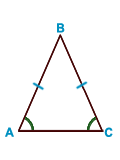 • в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой; • в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой; 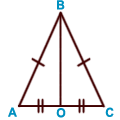  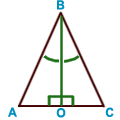 AB = BC (равнобедренный треугольник), AO = OC (BO — медиана), BO — общая сторона AB = BC (равнобедренный треугольник), AO = OC (BO — медиана), BO — общая сторона  ABO и ABO и  CBO. CBO.  ABO = ABO =  CBO по 3-му признаку. Следовательно: CBO по 3-му признаку. Следовательно: 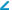 ABO = ABO = 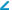 CBO. BO — биссектриса. CBO. BO — биссектриса. 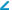 AOC — развернутый угол = 180°. AOC — развернутый угол = 180°. 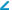 AOB = AOB = 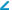 COB = COB =
= 90° . | ||
| Признаки равнобедренного треугольника: • если в треугольнике два угла равны, то он равнобедренный; • если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный; • если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный; • если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный. |
4) Сумма углов произвольного треугольника равна 180
Определение внешнего угла треугольника
Определение
Углы, смежные с углами треугольника, называются внешними.
Например, для 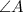 , внешними будут углы
, внешними будут углы 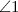 и
и 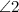 (см. рис.)
(см. рис.)
Свойства внешних углов треугольника
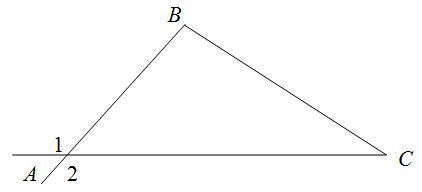
1. Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 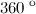 .
.
2. Сумма внешнего и внутреннего угла при одной вершине равна 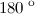 .
.
3. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
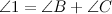
Угол.
Угол – это часть плоскости, ограниченная двумя лучами с общим началом.
Или
Угол – это геометрическая фигура, образованная двумя лучами с общим началом.
Биссектриса угла.
Биссектриса угла – это луч, выходящий из вершины угла, проходящий между его сторонами и делящий этот угол на два равных угла.
Развернутый угол.
Развернутый угол – это угол, стороны которого являются дополнительными лучами.
Прямой, тупой, острый углы.
Прямой угол – это половина развернутого угла;
тупой угол – это угол, больший прямого, но меньший развернутого;
острый угол – это угол, меньший прямого.
Единицы измерения углов.
Градусы, минуты, секунды (но не те, которыми измеряют время)
Определение смежных углов.
Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
Свойство смежных углов.
Сумма смежных углов равна 180°.
